This is the third “research” thread of the Polymath16 project to make progress on the Hadwiger–Nelson problem, continuing this post. This project is a follow-up to Aubrey de Grey’s breakthrough result that the chromatic number of the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki page.
Currently, our smallest 5-chromatic unit-distance graph has 803 vertices and 4144 edges. Much of the other progress has been in finding new 4- and 5-chromatic graphs, and hunting for features that make the chromatic number so large. I wanted to outline the role that algebraic structure appears to play in our progress to date:
Denote . Many of our constructions can be viewed as finite subsets of rings:
, known as the Eisenstein integers and the hexagonal lattice, is 3-chromatic.
contains 4-chromatic graphs such as the Moser spindle, Golomb’s graph (see this), and de Grey’s M. The entire ring appears to be 4-colorable by homomorphic coloring.
contains de Grey’s original 5-chromatic graph N.
contains 5-chromatic graphs due to Marijn and Tamás.
contains a 5-chromatic graph due to Jannis.
Let denote the set of complex numbers of unit modulus. Instead of
, several comments in the previous thread consider another ring
generated by
, where
and
. The inclusion of
is helpful since it appears in
:
Furthermore, by including the inverses of and
in
, these members are distinguished as units in the ring, making them easier to work with algebraically. In general, we want to keep track of which members of our ring have unit modulus, since these generate the edges in our Cayley graph.
Question. Given a subring of
, how do we identify the members of
?
Question. Is it the case that ?
By design, any ring containing and a complex number
of squared modulus
will also contain
. Tamás identified yet another member of
, and the corresponding edges are critical to the Cayley graph being 5-chromatic.
Once has been determined, one may hunt for homomorphic colorings of
.
Question. Does admit a homomorphic 5-coloring?
Question. Does there exist such that
does not admit a homomorphic 5-coloring?
In theory, we could use the absence of homomorphic colorings to flag the possible nonexistence of a coloring, and then run a SAT solver on a 3-fold (say) Minkowski sum of an appropriate finite subset of to establish nonexistence. (Warning: This may lead to many false positives considering the entire plane is not homomorphically colorable.)

As I had explored in the paper I posted in the second thread there are certain subsets of R^n that can demonstrably only be colored efficiently when using n-manifolds (After taking graph connectedness/disconnectness into account I’m not aware of any subset of R^n that requires manifolds with lower dimensionality than the containing space, only some that tolerate the presence of such, like R^n as a whole).
The chromatic color of a subset of R^n rises in jumps once we get past certain shapes and diamaters. Most simple example, if we consider any non-empty subset with diameter less than 1, it’s chromatic color is 1. My paper contains an example with 2 2-balls that has chromatic number 2 and explicitly requires the use of 2-manifolds, that is the according 2-balls. If we consider a 2-ball with diameter greater than 1 it jumps up to 3. This is the first time a 2-simplex emerges. As for the jump towards 4 I’m not sure. The latest point it could be to my knowledge is ~1.73, that is when the moser spindle first fits into the subset. If that’s the earliest point too then there’s likely some geometric significance at that number.
I’ll try to find out for myself at which points any subset begins tolerating lower dimensional manifdols, and if this relation ever switches around (which I doubt). Much closer to the initial goal of this project I also would like to find out at which respective diameters of a 2-ball subset the chromatic color switches over to 4 or 5 exactly, hoping this could give some insight into what type of structure it is that requires more colors.
Any ideas on this? Anyone able to provide me diameters of graphs that require 5 colors so I have some direction on that?
I think I found a couple first interesting links between my work on manifolds and finite unit distance graphs.
First of all: “If we consider a 2-ball with diameter greater than 1 it jumps up to 3. This is the first time a 2-simplex emerges.” That was of course wrong, must’ve been distraught when I brought up the 2-simplex so early.
If we consider a 2-ball subset of R^2, with diameter less than 2, as a unit distance graph then there’s always a center that consists entirely of discrete spaces/disconnected single nodes, these have no bearing on the chromatic number at all, so the relevant connected space is an annulus.
Assuming my theorem holds there’s a coloring using n-manifolds setting the upper boundary and a unit distance graph setting the lower bounds. Both can be made to agree to get a definitive answer on the chromatic number of euclidean spaces. Let’s consider a 2-ball of radius 0.55 (which means the disconnected center area has a diameter of 1-0.55=0.45), that is clearly 3-chromatic.
https://imgur.com/a/zrbA66k
We find that while the chromatic number of this subset is 3, a 2-simplex does not actually fit in this subset. Rather we get the chromatic number from a tesselation with manifolds and a pentagram. I would conjecture that as the outer diameter approaches 0.5 the length of the odd cycle probably goes beyond 5 and approaches infinity.
Now if we increase the radius until a 2-simplex fits in there I’m pretty sure the chromatic number also goes up to 4. As that happens the same manifold construction as before doesn’t work anymore since it then has an inner diameter of 1. Presumably there’s then a sort of cyclical structure emerging that creates a 4-chromatic finite unit distance graph, using 2-simplexes, probably with more and more vertices closer to infinity as we approach this new diameter from above. At this point I have no idea if that’ll generalize to higher diameters and chromatic numbers this nicely.
The questions would be, how would that structure work for a 4-chromatic graph, and where’s the transition to 5,6 and finally as I would think, 7 colors? How would this tie into a more generalizable solution? And could this help over a couple corners in finding 5-chromatic graphs with lower vertex count too? Just a wild conjecture, but if there exists such a formula that can produce smaller and smaller x-chromatic graphs with higher and higher vertex counts, the same might be done in reverse.
The smallest euclidean diameters for the current known 5-chromatic graphs is 4.5. I’d expect something less than 3, which is a very large gap however.
There is a factorisation trick that helps to solve the problem of finding elements of a ring of unit modulus. Suppose for example we are looking at a ring generated by two of these rotations. The ring will be inside a field![\mathbb{Q}[\sqrt{-p}, \sqrt{-q}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Csqrt%7B-p%7D%2C+%5Csqrt%7B-q%7D%5D+&bg=ffffff&fg=303030&s=0&c=20201002) so its elements are of the form
so its elements are of the form  where
where 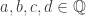
Expand the modulus squared . This needs to be equal to one but
. This needs to be equal to one but  is not a square so
is not a square so 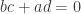 .
.
Solutions of this in rationals can be parameterised as for some rationals
for some rationals  which are not unique. Substituting these back gives an expression which factorises
which are not unique. Substituting these back gives an expression which factorises

In other words to find elements of unit modulus in a subring of![\mathbb{Q}[\sqrt{-p}, \sqrt{-q}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Csqrt%7B-p%7D%2C+%5Csqrt%7B-q%7D%5D+&bg=ffffff&fg=303030&s=0&c=20201002) you can look for elements in
you can look for elements in ![\mathbb{Q}[\sqrt{-p}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Csqrt%7B-p%7D%5D+&bg=ffffff&fg=303030&s=0&c=20201002) and
and ![\mathbb{Q}[\sqrt{-q}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Csqrt%7B-q%7D%5D+&bg=ffffff&fg=303030&s=0&c=20201002) whose products have unit modulus.
whose products have unit modulus.
This factorisation trick can be applied recursively with two field extensions at a time to show that if there are any number of generators, the elements of unit modulus will be products of elements from the fields with just one complex quadratic extension of the rationals.
https://arxiv.org/abs/1805.00157
Wow, I am delighted that there is so rapid a contribution by such superstars in the field. Geoffrey or Dan, if you’re reading, thank you for this. Just one tiny correction: you say “De Grey first constructs a graph of order 121 which contains 52 equilateral triangles of side length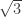 ” but actually there are 104, two in each hexagon.
” but actually there are 104, two in each hexagon.
It would be wonderful if you could offer some illumination here as to how you found your construction. Even though it is larger than those found by me and by others here, the method diverges in ways that might well synergise with those we are exploring thus far.
Everyone here: I think the graphs G_40 and G_49 in particular have great potential to be useful for us. Let’s explore.
Thank you Aubrey for your kind words and for noticing the typo. It will be fixed in the second version of the paper.
Geoffrey and I worked on this problem for the better part of the past three years. I will describe our thought process below.
Our first idea was that if we want to find a unit distance graph which is impossible to 4-color, we better find unit distance graphs which are difficult to 4-color.
Like you, we recognized the significance of the set of 30 unit vectors, denoted by V in your paper. We constructed various graphs which had high edge density, but as we all know by now, high edge density is not enough.
We eventually decided to analyze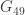 and some of its versions more closely. For instance, a certain supergraph of
and some of its versions more closely. For instance, a certain supergraph of 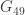 of order 73 has fractional chromatic number 383/102=3.759…For a while, we hoped we can find a unit distance graph with fractional chromatic number greater than 4 but that did not work.
of order 73 has fractional chromatic number 383/102=3.759…For a while, we hoped we can find a unit distance graph with fractional chromatic number greater than 4 but that did not work.
The graph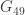 has 18694 4-colorings which is a manageable number. The next idea is to try to show that none of these colorings can be extended to the entire plane.
has 18694 4-colorings which is a manageable number. The next idea is to try to show that none of these colorings can be extended to the entire plane.
The obvious method is to add points whose colors are forced by the already colored points. More precisely, we add circumcenters of triples which are colored in three different colors if these points lie on a unit radius circumcircle, and hope that a color conflict will occur.
While many of the 4-colorings of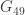 are easy to block in this manner, some are quite stubborn. Two things can happen: either one get stuck (no more circumcenters can be added) or the process seems to continue indefinitely with no conflict being achieved. I remember Geoffrey ran one of these colorings up to 200,000+ vertices and still no conflict appeared.
are easy to block in this manner, some are quite stubborn. Two things can happen: either one get stuck (no more circumcenters can be added) or the process seems to continue indefinitely with no conflict being achieved. I remember Geoffrey ran one of these colorings up to 200,000+ vertices and still no conflict appeared.
The next idea was to reduce the number of colorings we need to consider. For example, if vertices [-12,0,0,0] and [12,0,0,0] in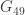 are colored the same, then we need to consider only 186 out of the 18694 colorings.
are colored the same, then we need to consider only 186 out of the 18694 colorings.
These two points are at distance from each other and one can assume they are identically colored because of the following fact: there exists a graph whose edges are
from each other and one can assume they are identically colored because of the following fact: there exists a graph whose edges are 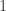 and
and  which cannot be 4-colored. We found such a graph of order 103.
which cannot be 4-colored. We found such a graph of order 103.
Out of these 186 remaining colorings, 150 can be easily blocked (via the add-circumcenter technique) but the rest of 36 are very difficult.
So rather than looking at monochromatic sets consisting of 2 points, we next considered sets of three points which appear monochromatic in the 18694 colorings of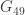 .
.
Equilateral triangles of side length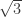 appear monochromatic in all but 94 of these colorings. On the other hand, equilateral triangles of side length
appear monochromatic in all but 94 of these colorings. On the other hand, equilateral triangles of side length 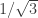 appear monochromatic in all but 44 of these colorings.
appear monochromatic in all but 44 of these colorings.
Moreover, in all these 44 surviving colorings, all the pairs distance apart have different colors.
apart have different colors.
Hence, if we can block a monochromatic triangle of side length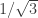 and show that for any 4-coloring contains two points
and show that for any 4-coloring contains two points  apart that are colored the same, we would be done.
apart that are colored the same, we would be done.
Fortunately, the first part can be achieved by adding circumcenters. We used a graph of order 627 to do this, although this is probably sub-optimal. We did not really try all that hard to improve this since we knew that the final graph is going to be huge anyway.
Finding a graph that forces a monochromatic pair distance apart was the tricky part. We tested lots of graphs and for each such candidate we tried to find patterns in their 4-colorings. Eventually, we noticed that certain pairs distance
apart was the tricky part. We tested lots of graphs and for each such candidate we tried to find patterns in their 4-colorings. Eventually, we noticed that certain pairs distance  apart would always be identically colored. From here, a simple spindle rotation of angle arccos(119/128) completes the job. (see the graphs
apart would always be identically colored. From here, a simple spindle rotation of angle arccos(119/128) completes the job. (see the graphs 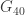 and
and  used to prove assertion (a)).
used to prove assertion (a)).
At this point one interesting question is whether this rotation can be avoided. In particular, is there a way to block the 44 colorings of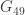 which do not contain a monochromatic
which do not contain a monochromatic 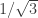 triple directly?
triple directly?
As mentioned in the paper, Madore proved that![\mathbb{Q}[\sqrt{3},\sqrt{11}] \times \mathbb{Q}[\sqrt{3},\sqrt{11}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Csqrt%7B3%7D%2C%5Csqrt%7B11%7D%5D+%5Ctimes+%5Cmathbb%7BQ%7D%5B%5Csqrt%7B3%7D%2C%5Csqrt%7B11%7D%5D&bg=ffffff&fg=303030&s=0&c=20201002) can be
can be  -colored. As Dustin asked in one of his posts, it would be nice to decide if the chromatic number of this subfield is 5.
-colored. As Dustin asked in one of his posts, it would be nice to decide if the chromatic number of this subfield is 5.
[Edited to fix the LaTeX rendering. – M.]
Dan, thank you so much for this detailed account. I feel terribly guilty about scooping you after you put in all this work! It looks as though I got lucky and you got unlucky in a couple of key ways: (a) I started from a 97-vertex graph with 78 spindles and not many colourings that have mono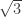 triangles, whereas by starting from G_49 you were seduced into looking at triangles of edge
triangles, whereas by starting from G_49 you were seduced into looking at triangles of edge  rather than
rather than 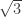 , and (b) when moving to progressively larger graphs I chose to maintain hexagonal symmetry, purely for computational efficiency reasons but it seems also to have been a simpler way to achieve particular constraints.
, and (b) when moving to progressively larger graphs I chose to maintain hexagonal symmetry, purely for computational efficiency reasons but it seems also to have been a simpler way to achieve particular constraints.
You mention a 103-vertex UD graph that can be rendered 5-chromatic by constraining all its vertex pairs that are at separation to be bichromatic. This could be extremely useful – can you show us that graph please? The only UD graph I have found that has just one non-unit distance and which would become 5-chromatic if that distance were made a “virtual edge” (as we’ve come to call it here) is the regular pentagon, and I think it would be great to have a catalogue of other examples. We are also interested in cases where there is exactly one vertex pair at a second non-unit separation, since two copies of such a graph in which all instances of the first non-unit separation have been “virtualised” can be joined in a spindle; so far we have three examples of that. (all with just five vertices). Similarly, as we’ve both found, it would be valuable to find graphs in which all 4-colourings make a particular equilateral triangle monochromatic (or in which no 4-colouring does). Beyond that, as we’ve also both seen, there’s the weaker case where all 4-colourings feature at least one of a bunch of pairs (or triangles) being mono. My sense is that if we build up a nice large catalogue of graphs with properties of these types, we will not only identify a nice range of 5-chromatic cases: we will also have a shot at identifying 5-chromatic cases which themselves have such constraints (in relation to all 5-colourings), which of course would be a huge step towards finding a 6-chromatic case. Some first steps in this direction have already been mentioned by others here.
to be bichromatic. This could be extremely useful – can you show us that graph please? The only UD graph I have found that has just one non-unit distance and which would become 5-chromatic if that distance were made a “virtual edge” (as we’ve come to call it here) is the regular pentagon, and I think it would be great to have a catalogue of other examples. We are also interested in cases where there is exactly one vertex pair at a second non-unit separation, since two copies of such a graph in which all instances of the first non-unit separation have been “virtualised” can be joined in a spindle; so far we have three examples of that. (all with just five vertices). Similarly, as we’ve both found, it would be valuable to find graphs in which all 4-colourings make a particular equilateral triangle monochromatic (or in which no 4-colouring does). Beyond that, as we’ve also both seen, there’s the weaker case where all 4-colourings feature at least one of a bunch of pairs (or triangles) being mono. My sense is that if we build up a nice large catalogue of graphs with properties of these types, we will not only identify a nice range of 5-chromatic cases: we will also have a shot at identifying 5-chromatic cases which themselves have such constraints (in relation to all 5-colourings), which of course would be a huge step towards finding a 6-chromatic case. Some first steps in this direction have already been mentioned by others here.
Given the they are getting the same ring
they are getting the same ring ![\mathbb{Z}[\omega_1, \omega_3, \omega_{64/9}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Comega_1%2C+%5Comega_3%2C+%5Comega_%7B64%2F9%7D%5D+&bg=ffffff&fg=303030&s=0&c=20201002)
However they are rotating on a spindle of length rather than
rather than 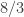
No reason to feel guilty Aubrey. Judging by the latest discussions it appears that other people were also close to a solution. The problem was ripe for the picking. And while we like your proof better, we are very happy that ours is different.
Regarding the situation when we forbid two distinct distances from appearing monochromatic, we already considered the problem and we have a few results ready. We will upload the paper on arxiv within the next few days. But until then, here is a summary of our findings.
Suppose one wants to color the plane such that no two points distance 1 or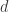 apart can be colored identically. We prove that at least five colors are needed if
apart can be colored identically. We prove that at least five colors are needed if 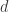 is taking any of the following values:
is taking any of the following values:
As for the 3-dimensional case, we looked into that as well. We refined Nechushtan’s approach and managed to construct an explicit 6-chromatic unit distance graph in of order 79. We will post that paper on arxiv sometimes this week.
of order 79. We will post that paper on arxiv sometimes this week.
[Edited to fix the LaTeX rendering. – M.]
Many thanks again Dan. Concerning the distances that force 5-chromaticity when combined with 1, I’m surprised not to see them forming pairs {d,1/d}, given the scaling argument noted here earlier by Nazgand. Is there a flaw in that argument?
As for R^3, I am really looking forward to seeing your 79-vertex construction. The 60-vertex one that I described at
can be reduced to 59 in a bunch of ways by rotation, so I’m wondering whether your graph uses the same 20-vertex building-block as mine, just with four of them rather than three.
Thanks again Dan. I just wanted to make sure I wasn’t missing something obvious regarding reciprocals of your values. So I can then add (and their reciprocals) to your list, via the nine-vertex graphs formed by spindling the unique distance in each of the graphs I described here:
(and their reciprocals) to your list, via the nine-vertex graphs formed by spindling the unique distance in each of the graphs I described here:
Wait, can’t we spindle their graph in Claim 2.1 to get a 5-chromatic graph with only 157 vertices??
Ah, no – the monochromatic pair is not fixed. For every coloring, *there exists* a monochromatic pair. This graph is playing the role of Aubrey’s L.
Still, the result follows from Claim 2.1, since you can spindle all of those pairs. I wonder how close this is to a human proof. The only thing to check is the “crucial property of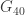 ” given in the first line of page 3. This is a property about all 4-colorings of a graph with 40 vertices. Since this is reminiscent of Aubrey’s L (which was provable by hand), I suspect this is within reach. The first step would be to find a simpler representation of the graph (perhaps a planar embedding?) and identify the pairs of vertices that are
” given in the first line of page 3. This is a property about all 4-colorings of a graph with 40 vertices. Since this is reminiscent of Aubrey’s L (which was provable by hand), I suspect this is within reach. The first step would be to find a simpler representation of the graph (perhaps a planar embedding?) and identify the pairs of vertices that are  apart in the unit-distance embedding. In fact, when checking this property, it is more natural to add edges between vertices that are
apart in the unit-distance embedding. In fact, when checking this property, it is more natural to add edges between vertices that are  apart.
apart.
EDIT: You can’t just spindle all of those pairs. Spindling only works when you force a fixed pair to be monochromatic.
Hey Aubrey, I apologize for the delayed reply. I did not have time to follow all the comments (last week of the semester is coming), but here is what I have.
First a definition: given a positive real number $d$ different from $1$, a $\{1,d\}-graph$ is a finite graph whose vertices are points in the plane and whose edges are obtained by connecting two points whenever the distance between them is either $1$ or $d$. (I do not have a particular preference towards the term “virtual edge” so I am avoiding it).
The goal is to construct small $5$-chromatic $\{1,d\}$-graphs for various values of $d$. Note that a $\{1,d\}$-graph can be transformed into a $\{1, 1/d\}$-graph after an appropriate scaling (I believe this is the gist of one of Nazgand’s comments).
For this reason, we can only consider the case $d>1$.
Note that all the values of $d$ listed in my previous post satisfy this inequality.
We will upload the paper tomorrow; it should be up within the next couple of day.
Thank you for drawing my attention to your 3-d construction. I will try to look at it today.
To cut to the chase, the most obvious point to use as a spindal to possibly force a 6 colouring is (5/3, 0) This is already a multiple of 5 in the ring![\mathbb{Z}[\omega_1, \omega_3]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Comega_1%2C+%5Comega_3%5D&bg=ffffff&fg=303030&s=0&c=20201002) so it will be the same colour as the origin in any homomorphic 5-colouring. It arises as
so it will be the same colour as the origin in any homomorphic 5-colouring. It arises as 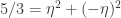 so it is already available in
so it is already available in 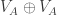 .
.
What happens if we combine all the vectors in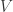 and
and 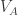 to form
to form  (did we use the letter Z already?), then look at
(did we use the letter Z already?), then look at  ? Is the point at 5/3 always the same colour as the origin in any 5-colouring ? It seems a long shot, but worth checking.
? Is the point at 5/3 always the same colour as the origin in any 5-colouring ? It seems a long shot, but worth checking.
Form from the unit modulus numbers
from the unit modulus numbers  with
with 
Then take the graph . Is the point 5/3 always the same colour as the origin for all 5-colourings in this graph?
. Is the point 5/3 always the same colour as the origin for all 5-colourings in this graph?
If not, how about using instead of
instead of 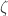
These graphs are probably too large so what subgraph might work?
Just curious, is it now possible to find a construction to show that no matter how we color the plane in 3 colors, there exists an equilateral triangle with side length 1 with vertices of the same color? This is a stronger statement, because 5-coloring of the plane will follow from it.
Sorry for the wrong statement. I just realized that it is not even true for two colors.
Right, as was observed by Erdos et al. here:
https://www.sciencedirect.com/science/article/pii/0097316573900113
They show that it is true for 2 colors in 3 dimensions, though!
What’s the smallest virtual edge we’ve observed so far? I’m aware of . Has anyone found a virtual edge with length
. Has anyone found a virtual edge with length 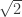 already?
already?
Nevermind the first part of the question. I’d still be interested if there’s a virtual edge of length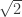 .
.
Could someone tell me the exact definition of ‘virtual edge’?
We’re using “virtual edge” to denote a length d != 1 that is the separation between one or more pairs of vertices v_i,,w_i of a graph G, such that in all 4-colourings of G at least one such pair is monochromatic. The utility of this concept arises when we also have a graph H in all of whose 4-colourings a specific pair of vertices v,w at separation d is bichromatic. The name arises because we can then force all pairs v_i,w_i in G to be bichromatic by identifying each pair with v,w of a copy of H (which I’ve been calling “clamping”), thereby arriving at a 5-chromatic graph with one subgraph that is a copy of G and >=1 subgraphs that are copies of H. I have a feeling we’ll be expanding this vocabulary as the project progresses.
I think it’d be very useful to have these new terms clearly listed in the wiki page. I’ve gotten the gist of what a virtual edge is while looking for connections to manifold tesselations, hence my question above as I would assume there’s a virtual edge with the length specified above, but none that are smaller.
But I have to admit I did search the wiki page for a definition of a virtual edge once, and didn’t find it.
I’ve now added a section on the wiki on virtual edges; there may be more known examples of graphs with virtual edges, so feel free to add to the list provided. Also I have expanded the list of unit graphs to also list the new graphs used in the Exoo-Ismailescu paper, and to list also the additive group that various graphs are known to lie in. There are still a lot of gaps in the table, feel free to fill them in yourself (or post any additions here and I will get around to putting them in).
I see! This definition is highly counter-intuitive for me; I would expect an edge to go between two differently colored vertices, and not two monochromatic vertices. Can we have a discussion about changing this notion until it’s not too late? I would call this something like graph ‘missing a virtual edge’ (length) to be 5-chromatic.
When we have started working with Tamas on Hadwiger-Nelson last year, we were also looking for such structures, but I think that we’ve called ‘virtual edge’ exactly what you have in H above, as it behaves exactly like an edge. In fact, once we have such an H for a given distance d, then we’re practically looking for graphs where the length of every edge is 1 or d and have a high chromatic number. These have been studied a lot, see e.g. this paper by Bukh: https://arxiv.org/pdf/math/0703856.pdf
I also propose that at the wiki page we should list not only the G’s, but also the H’s under the section ‘virtual edge’.
I concur, it’s a bit confusing to have a normal edge and a virtual edge mean the opposite in regards to forcing/excluding a color, and doesn’t strike me as the best notation. I’d rather say a virtual edge should be what it sounds like, that is a distance for which there exists a structure that forces two vertices at this distance to have different colors. Then I also heard mentions of monochromatic pairs/edges before, which would then be structures that force two into the same color. (Hoping I got that right.)
The definition should also be cleanly generalized as early as possible. Right now the virtual edge section refers explicitly to 4-colorings of G, and I doubt that’s where this definition really begins or ends. Aside from the relevance of the dimensionality of the space we’re talking about, most importantly we should early define how exactly the current number of colors plays into this. For instance the 4-vertex diamond has a monochromatic pair/edge under the assumption of 3 colors, but not 4 or more.
Yeah, we need to tighten up this definition. In my original, perhaps over-hasty, wording I decribed the virtual edge as a distance that exists in both G and H, such that in G in is always mono and in H it is never mono. I think you folks are right though: we should define the term in terms of a specific graph, and that graph should be the one I termed H in my definition. Could someone with better mathematical vernacular please have a go
I walked through the “clumsy and not too impressive” argument mentioned at the end of Pritikin’s [1] with Hans Parshall this afternoon, and we obtained the following result:
Every unit-distance graph with at most 16 vertices is 5-colorable.
I’m not sure if Pritikin’s general technique of finding so-called “good 6-colorings” can improve this guarantee, but at least we have a baseline now.
Speaking of Pritikin’s paper, I did a symbolic optimization of the shape he uses, and it only pushes the number to about 6197.5.
One can view his heptagonal+diamond tiling as arising from a shifted square tiling. Start with the usual periodic square tiling. Shift every third and fourth row over by 1/2. Now color the rows successively using 1,2,3,1,2,3… and 4,5,6,4,5,6…, but shifted appropriately. Then cut off corners to avoid unit distances, and where possible enlarge the resulting octogons into heptagons.
It is possible to correct the order N=16:
Every unit-distance graph with at most N=24 vertices is k=5-colorable.
To get N=16 for 5-coloring one can start from optimal case for 4-coloring with N=12 and place an additional tile to fix every 2 of 8 triangle holes of initial coloring.
It is easy to reach the value N=21, replacing one tile of initial 4-coloring by two tiles symmetrically and adjusting an offset from replaced tile.
To get N=24 many tricks were used. The final optimization procedure had 16 parameters (degrees of freedom) and a lot of equations and weak constraints. The result is very close to N=25. There are some ideas, and maybe this value could be reached.
It is possible also to adjust the Pritikin’s bounds for 6-colorable graphs a little bit (about 10%).
https://drive.google.com/open?id=1_qELb0Kx0wi4hL13CaT4857fHCNsoPuZ
N=12, k=4
The pictures for cases of N=16, N=21 and N=24 are here:
https://drive.google.com/open?id=1OqbeLBGW56TLgQ4cIY-mRia4pWaOxOK1
https://drive.google.com/open?id=1gJOt5jcxy7Iaou88AJq4qnuRSCIw6C3a
https://drive.google.com/open?id=1IG57N11-lRH40Tu-1BDY-8PxWowqAP4s
@Jaan – Interesting! How did you formulate the optimization?
@Jaan – wow, this is outstanding! I agree that your way to get to 21 is easy and I’m annoyed with myself for not spotting it – but your 24er is a joy to behold. I’m honestly surprised that you were able to define it with as few as 16 parameters; I bet you are right that further small improvements are possible. Exactly how close to 0.96 (well, to some number of significant digits!) are you with this tiling?
Also, could you please clarify what you mean by your last comment? Do you mean you have improved Pritikin’s tiling to give a lower bound of nearly 7000 vertices? It would be great to see a visualisation of that.
One more thing: in the nearly three months since the original posts, there have been six rollovers of the overall Polymath16 discussion, so your new posts are a bit hard to find for those who are not signed up to receive alerts. To fix that, I will now make a brief post on the current thread:
pointing to your first post and linking to your figures. Then it would be best if you could post any subsequent messages as replies to that post of mine.
@ag24 It’s not that hard because of the commentroll on the blog.
Fair enough – but hey, it’s also an excuse to re-enliven the current thread, which has been quiet for a while.
All tiles are placed according to the grid (triangular in our case) with some offsets for every color. The tiles of a given color have two main constraints: inner (the width of a tile in any direction should be less than 1) and outer (the distance between any two tiles should be more than 1).
The tiles have their own shape for every color. Every tile is broken into several elements (sectors and polygons). It helps to extend the “effective diameter” of a tile. Every element is described by a set of inequalities and has their own degrees of freedom.
The maximized function is a relative area of all tiles. In common the parameters of optimization are grid parameters, relative coordinates of tile origins, offsets and orientations of tile elements. Due to internal symmetry of final tiling, many parameters depend to each other, this helps to reduce the final number of optimization parameters. After each optimization step one can remove some constraints or introduce some additional elements to the tile shapes.
My final record was 24.843.
The case of 6-coloring is simpler, because all tiles have the same shape.
One can use the following tricks to adjust the graph order N: modify the shape of existing diamonds, introduce some other diamonds, use 15-vertex polygons instead of heptagons, attach round segments to some edges.
After optimization of polygon parameters N=6899. After attaching of segments N=6906. So,
All unit-distance graphs of order N=6906 are 6-colorable.
The construction for 6-coloring is shown here:
https://drive.google.com/open?id=1AsOb7GDImtLMjQL0AR-4fFP7uuc37wy8
All holes are increased many times of course. The real coloring is visually just a set of pentagons.
Thanks! Terrific. Could you please repost these on the new thread?
I just noticed that the wiki says a virtual edge is a pair which is monochromatic rather than non-monochromatic. Edges of length 1 are non-monochrome, thus virtual edges were also meant to be non-monochrome.
I want to edit the wiki to more clearly express the concepts, yet am not able to create an account.
It is known that the existence monochromatic virtual edges of length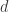 and chromatic number
and chromatic number  are proof that
are proof that  : create a triangle with edges
: create a triangle with edges  for some integer
for some integer 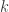 large enough for the triangle to exist.
large enough for the triangle to exist.
Recently I noticed a possible proof that non-monochromatic virtual edges of length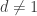 and chromatic number
and chromatic number  also prove
also prove  . I have not figured out how to make it rigorous, but the main idea is: Consider the problem of coloring the complex plane, such that no points distance 1 apart may be the same color. I.e.
. I have not figured out how to make it rigorous, but the main idea is: Consider the problem of coloring the complex plane, such that no points distance 1 apart may be the same color. I.e.
Note for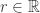 ,
,
Suppose we could deduce a virtual non-monochromatic edge length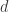 of chromatic number
of chromatic number  :
:
From above, it seems we should also be able to deduce , which would mean every point is a unique color or the chromatic number of the plane is larger than
, which would mean every point is a unique color or the chromatic number of the plane is larger than  .
.
To be clear, by non-monochromatic virtual edge length d of chromatic number a, I mean a graph H_0 with a specific pair distance d apart which cannot be the same colour for any a-coloring of H_0.
By monochromatic virtual edge length d of chromatic number a, I mean a graph H_1 with a specific pair distance d apart which must be the same colour for every a-coloring of H_1.
Clamping may be used to obtain more non-monochromatic virtual edges, which may be helpful for finding a 6-chromatic graph. be a graph with a specific pair of vertices length
be a graph with a specific pair of vertices length  apart that are unable to be colored the same for any
apart that are unable to be colored the same for any  -coloring of
-coloring of  .
.
Let
Multiplicative property of non-monochrome virtual edges: Let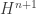 be the graph
be the graph  with every unit edge replaced with a copy of
with every unit edge replaced with a copy of  , thus producing a virtual edge length
, thus producing a virtual edge length 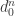 .
.
Extending The idea of graph G in the wiki, let G be such that every -coloring of G has either (a monochrome pair of vertices length
-coloring of G has either (a monochrome pair of vertices length 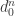 apart for some positive integer
apart for some positive integer 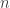 ) or (a specific pair of vertices length
) or (a specific pair of vertices length  apart that are unable to be colored the same for any
apart that are unable to be colored the same for any  -coloring of G which does not have the aforementioned monochrome pairs).
-coloring of G which does not have the aforementioned monochrome pairs).
Clamping G with at every set of vertices length
at every set of vertices length 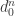 apart produces a non-monochromatic virtual edge length
apart produces a non-monochromatic virtual edge length  of chromatic number
of chromatic number  .
.
To set up an account to edit the wiki, you have to email mn@michaelnielsen.org
My definition of “virtual edge” was drawn from Audrey’s previous comment at https://dustingmixon.wordpress.com/2018/05/01/polymath16-third-thread-is-6-chromatic-within-reach/#comment-4172 , but now it seems that people are actually using “virtual edge” in slightly different ways. A priori one could consider four concepts which could conceivably be called a (4-coloring) “virtual edge” of a graph G:
1. A distance d such that for any 4-coloring of G, at least one pair of vertices in G at distance d apart is forced to be monochromatic.
2. A pair of vertices in G at distance d apart such that for any 4-coloring of G, that specific pair of vertices is forced to be monochromatic.
3. A distance d such that for any 4-coloring of G, at least one pair of vertices in G at distance d apart is forced to be bichromatic.
4. A pair of vertices in G at distance d apart such that for any 4-coloring of G, that specific pair of vertices is forced to be bichromatic.
The clamping argument shows that we can show that the plane is not 4-colorable if we can find a distance d that obeys property 2 for one graph G and property 3 for another graph H, or property 1 for one graph G and property 4 for another graph H.
The isosceles d,d,1 triangle already obeys property 3, so as soon as there is any graph G that obeys property 2 for one distance d, we are done; this is the spindling argument.
I was using the term “virtual edge” to refer to property 1, but it appears there is not a consensus on this matter. I guess we should discuss things further.
Perhaps we could borrow terminology from Euclidean Ramsey theory: Given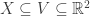 , we could (for example) say X is k-monochromatic Ramsey in V if for every proper k-coloring of
, we could (for example) say X is k-monochromatic Ramsey in V if for every proper k-coloring of 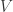 , there exists a monochromatic set congruent to X in V.
, there exists a monochromatic set congruent to X in V.
I like this suggestion. Here is an expanded proposal:
1. A pattern is a
is a 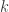 -monochromatic Ramsey pattern of a graph
-monochromatic Ramsey pattern of a graph  if every
if every 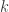 -coloring of
-coloring of  contains a monochromatic copy of
contains a monochromatic copy of  .
.
2. A subgraph of
of  is a
is a 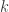 -monochromatic subgraph if every
-monochromatic subgraph if every 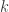 -coloring of
-coloring of  has
has  monochromatic. (Thus, every k-monochromatic subgraph is a k-monochromatic Ramsey pattern, but the converse is not true.)
monochromatic. (Thus, every k-monochromatic subgraph is a k-monochromatic Ramsey pattern, but the converse is not true.)
We also can replace “monochromatic” by “bichromatic”, “polychromatic”, etc..
Example: the long diagonal of a unit rhombus is a 3-monochromatic subgraph but not a 4-monochromatic subgraph.
In Aubrey’s graph L, the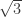 -equilateral triangle is a 4-monochromatic Ramsey pattern, but not a 4-monochromatic subgraph. In Aubrey’s graph N, the same triangle is a 4-polychromatic subgraph. Combining the two gives a non-4-colorable graph.
-equilateral triangle is a 4-monochromatic Ramsey pattern, but not a 4-monochromatic subgraph. In Aubrey’s graph N, the same triangle is a 4-polychromatic subgraph. Combining the two gives a non-4-colorable graph.
The graph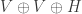 has a 4-monochromatic subgraph that is an edge of length 8/3; also, the
has a 4-monochromatic subgraph that is an edge of length 8/3; also, the 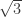 -triangle is again a 4-polychromatic subgraph.
-triangle is again a 4-polychromatic subgraph.
The case of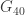 is interesting. It has sort of a hybrid between a 4-bichromatic pattern (the edge of length
is interesting. It has sort of a hybrid between a 4-bichromatic pattern (the edge of length  ) and a 4-monochromatic subgraph (an edge of length 8/3). Namely, in any 4-coloring of
) and a 4-monochromatic subgraph (an edge of length 8/3). Namely, in any 4-coloring of 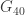 , either the given 8/3-edge is monochromatic, or there is a bichromatic edge of length
, either the given 8/3-edge is monochromatic, or there is a bichromatic edge of length  . Aubrey’s graph K has a similar property. This is perhaps too complicated of a property to try to describe with a single notation. (It has a nice interpretation though in probabilistic language, see Lemma 7 and Lemma 3.)
. Aubrey’s graph K has a similar property. This is perhaps too complicated of a property to try to describe with a single notation. (It has a nice interpretation though in probabilistic language, see Lemma 7 and Lemma 3.)
Looks much clearer to me than the previously used notation. It’s almost obvious what’s meant at a first glance without looking at your explanations 1. and 2., and looking at those clears up the rest quickly.
If cases such as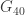 become too numerous/too complex so that their descriptions bloat papers/posts it shouldn’t be too hard to put the logical connections into shorter symbolic notation, which I would assume to be sufficient. A general attempt at putting such properties into a single notation likewise strikes me as overcomplicating things rather than simplifying.
become too numerous/too complex so that their descriptions bloat papers/posts it shouldn’t be too hard to put the logical connections into shorter symbolic notation, which I would assume to be sufficient. A general attempt at putting such properties into a single notation likewise strikes me as overcomplicating things rather than simplifying.
In the definition of a virtual edge in the wiki, it says clamp a copy of H to EVERY virtual edge in G to increase the chromatic number from 4 to 5. Isn’t clamping H to any such virtual edge in G sufficient?
As currently defined, if d is a virtual edge distance for G, this means that there is some family of edges in G at distance d apart, such that for any 4-coloring of G, at least one of the edges will be monochromatic, but one cannot specify in advance which one it will be. So one has to clamp a copy of H to each such edge to eliminate all 4-colorings. But it seems there is not a consensus at present as to whether this is what we should be calling a “virtual edge”. Alternate naming suggestions are welcome.
Okay, in current – but maybe not future – usage, a virtual edge is a distance, not a particular pair of vertices.
Relating to the discussion of virtual edges, I think it may be profitable to recast the arguments in probabilistic notation, as (a) it allows one to combine results from multiple graphs together cleanly without having to explicitly spindle, clamp, or Minkowski sum the graphs, and (b) it also introduces the possibility of using upper and lower bounds on probability that involve numbers other than 0 or 1 that may lead to a more efficient (and human-verifiable) proof.
Let me explain. Suppose we have a given (deterministic) 4-coloring of the plane. Then we can apply any Euclidean isometry (translation, rotation, and/or reflection) to obtain another 4-coloring
of the plane. Then we can apply any Euclidean isometry (translation, rotation, and/or reflection) to obtain another 4-coloring 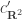 of the plane; we can also permute the 4 colors randomly. Let
of the plane; we can also permute the 4 colors randomly. Let  denote a random 4-coloring obtained by starting with the deterministic 4-coloring and applying a random Euclidean isometry, chosen “uniformly” amongst all such isometries, as well as a random permutation of the colors. Strictly speaking, this doesn’t make sense because the Euclidean isometry group is non-compact (and so does not have a Haar probability measure). However by using the device of ultrafilters, it is possible to make this concept rigorous, at the cost of making the probability measure only finitely additive rather than countably additive. I might detail this in the wiki at some point (it is also related to how one proves the de Bruijn-Erdos theorem). But if we set aside these technical difficulties, we obtain a random coloring
denote a random 4-coloring obtained by starting with the deterministic 4-coloring and applying a random Euclidean isometry, chosen “uniformly” amongst all such isometries, as well as a random permutation of the colors. Strictly speaking, this doesn’t make sense because the Euclidean isometry group is non-compact (and so does not have a Haar probability measure). However by using the device of ultrafilters, it is possible to make this concept rigorous, at the cost of making the probability measure only finitely additive rather than countably additive. I might detail this in the wiki at some point (it is also related to how one proves the de Bruijn-Erdos theorem). But if we set aside these technical difficulties, we obtain a random coloring  .
.
Next, for any finite unit distance graph , and any 4-coloring
, and any 4-coloring 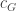 of that graph, we can define the coloring probability
of that graph, we can define the coloring probability  to be the probability that the random coloring
to be the probability that the random coloring  , when restricted to
, when restricted to  , gives the coloring
, gives the coloring 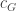 . These are numbers between 0 and 1 that obey the usual laws of probability, for instance
. These are numbers between 0 and 1 that obey the usual laws of probability, for instance  must sum to 1 when
must sum to 1 when 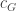 ranges over all the possible 4-colorings of
ranges over all the possible 4-colorings of  . But, because of the invariance properties of
. But, because of the invariance properties of  , we have the additional symmetry property: the coloring probabilities are invariant under Euclidean isometries of
, we have the additional symmetry property: the coloring probabilities are invariant under Euclidean isometries of  and also under relabeling of the colors in
and also under relabeling of the colors in 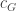 . This already lets us compute several of the simplest coloring probabilities exactly. For instance, for a single vertex such as the origin
. This already lets us compute several of the simplest coloring probabilities exactly. For instance, for a single vertex such as the origin 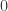 , and calling the colors
, and calling the colors  , all of the probabilities
, all of the probabilities  for
for  must match and sum to one, thus
must match and sum to one, thus 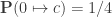 for
for  . Similarly, given a unit edge such as
. Similarly, given a unit edge such as  , we have
, we have  in a 4-coloring, and all the other probabilities
in a 4-coloring, and all the other probabilities  are equal to each other, hence
are equal to each other, hence 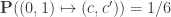 for all
for all  .
.
Here is the spindling argument in this language. Suppose we could find a distance d and a unit distance graph G such that there is a pair of vertices d apart in G that are forced to be monochromatic. Rotating this pair to be 0 and d in the complex plane, we thus have (or equivalently
(or equivalently 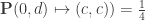 for
for  . On the other hand, if
. On the other hand, if 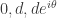 are vertices of a
are vertices of a  -triangle, then
-triangle, then 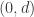 and
and  cannot both be monochromatic, thus by invariance
cannot both be monochromatic, thus by invariance  . This gives a contradiction.
. This gives a contradiction.
Similarly: Aubrey's original graph L has the property that any 4-coloring of it must have one of the 52 copies of H contain a monochromatic triangle. This implies that .
. , we conclude that
, we conclude that  . On the other hand, Aubrey's graph
. On the other hand, Aubrey's graph 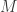 is a graph containing (say)
is a graph containing (say)  with the property that no 4-coloring of this graph makes this triangle monochromatic, thus
with the property that no 4-coloring of this graph makes this triangle monochromatic, thus 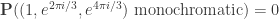 . This gives a contradiction.
. This gives a contradiction.
Taking a specific monochromatic triangle
The point is now that we can start hunting for more upper and lower bounds for probabilities like this, with each unit distance graph potentially providing a new inequality. One could imagine collecting all these inequalities into a database, and eventually there may be enough human-verifiable such inequalities that one could use linear programming to obtain a human-verifiable contradiction. I think there is scope to take numerical advantage of the fact that we can bound several probabilities by explicit fractions between 0 and 1; so far our arguments have only been deterministic in nature in that one has only distinguished between events that occur with probability 0 (impossible events), 1 (forced events), or between 0 and 1 (indeterminate).
potentially providing a new inequality. One could imagine collecting all these inequalities into a database, and eventually there may be enough human-verifiable such inequalities that one could use linear programming to obtain a human-verifiable contradiction. I think there is scope to take numerical advantage of the fact that we can bound several probabilities by explicit fractions between 0 and 1; so far our arguments have only been deterministic in nature in that one has only distinguished between events that occur with probability 0 (impossible events), 1 (forced events), or between 0 and 1 (indeterminate).
The proposed approach assumes there is a 4-coloring of the plane, draws a “random” isometry of the plane to produce a random 4-coloring
of the plane, draws a “random” isometry of the plane to produce a random 4-coloring  , and then derives contradictory probability estimates. In order for this argument to go through, must
, and then derives contradictory probability estimates. In order for this argument to go through, must  be measurable?
be measurable?
Here’s a compact example that gives me pause:
Given any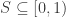 , let
, let 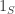 denote the indicator function of
denote the indicator function of  . Since the group of translations modulo 1 is compact, we may draw a random translation
. Since the group of translations modulo 1 is compact, we may draw a random translation  . It appears that
. It appears that
defines a measure over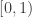 , and in fact
, and in fact  equals the Lebesgue measure of
equals the Lebesgue measure of  . As such, the probability wouldn’t exist when
. As such, the probability wouldn’t exist when  is non-measurable.
is non-measurable.
I think that the measure is not the standard one. For amenable groups, there is a finitely additive measure such that every subset is measurable.
@domotorp – That’s why I focused on the compact case, where the measure is the standard one. In this case, you can only talk about probabilities when the original coloring is measurable. Does the non-compact amenable case avoid this problem?
I’m not an expert on amenable groups, but I think that even in the compact case you get a (finitely additive) measure where every subset is measurable.
I see. It seems that I have a finitely additive measure that agrees with Lebesgue on measurable sets.
I went through the exercise of interpreting the main results of Exoo and Ismailescu [1] in your probabilistic notation:
Claim 2.1.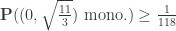
Claim 3.1.
Claim 4.1.
Combining these produces a contradiction:
I’ve now started a wiki subpage http://michaelnielsen.org/polymath1/index.php?title=Probabilistic_formulation_of_Hadwiger-Nelson_problem in which I collect this argument and all the other probabilistic inequalities I am currently aware of, making a distinction between human verifiable, potentially human-verifiable, and computer-verifiable claims. Hopefully we can start adding to this list (particularly in the first two categories).
One concrete possibility: since for any
for any 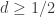 by the spindle argument, if we can find a graph
by the spindle argument, if we can find a graph  and a family of edges of length d such that any 4-coloring of G will make more than half of these edges monochromatic, then we will get the desired contradiction. For instance if can identify three such edges such that at least two of the three have to be monochromatic then we are done. Maybe this is easier than forcing a single such edge to be monochromatic?
and a family of edges of length d such that any 4-coloring of G will make more than half of these edges monochromatic, then we will get the desired contradiction. For instance if can identify three such edges such that at least two of the three have to be monochromatic then we are done. Maybe this is easier than forcing a single such edge to be monochromatic?
It also seems to me that the Pritikin type constructions should be describable in this probabilistic language. It may also be combinable with the Falconer arguments for the measurable problem, though I haven’t thought carefully about this.
A potentially useful generalisation of what I said in the second paragraph: the edges in the family don’t need to be the same length! So for instance if there are three edges, each of length at least 1/2, in G, but potentially of differing lengths, and any 4-coloring of G makes at least two of these edges monochromatic, then we are done.
I can improve the bound of 1/2 in the spindle argument in some cases. For instance I can show that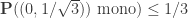 , by considering the unit equilateral triangle together with its center, which is a distance
, by considering the unit equilateral triangle together with its center, which is a distance 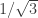 from all three vertices. At most one of the vertices of the triangle can be monochromatic with its center, giving the claim. There are a few other distances for which this argument works, see Lemma 12 of http://michaelnielsen.org/polymath1/index.php?title=Probabilistic_formulation_of_Hadwiger-Nelson_problem .
from all three vertices. At most one of the vertices of the triangle can be monochromatic with its center, giving the claim. There are a few other distances for which this argument works, see Lemma 12 of http://michaelnielsen.org/polymath1/index.php?title=Probabilistic_formulation_of_Hadwiger-Nelson_problem .
This implies for instance that if we can find another graph which has two pairs of edges, one of length
which has two pairs of edges, one of length 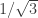 and the other of length at least 1/2, and at least one of these is forced to be monochromatic, then we are done (since 1/3 + 1/2 < 1).
and the other of length at least 1/2, and at least one of these is forced to be monochromatic, then we are done (since 1/3 + 1/2 < 1).
The spindle argument be improved like so: if all point pairs distance d apart must be monochrome, then all point pairs distance distance k*d apart must also be monochrome for positive integers k. Choose k such that k*d>1/2.
By considering the four essentially different colorings of H, one can obtain the surprisingly large bound
see Lemma 15 of http://michaelnielsen.org/polymath1/index.php?title=Probabilistic_formulation_of_Hadwiger-Nelson_problem . As a consequence, if one can find a unit distance graph G with a bunch of 2-edges and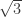 -edges, with the property that the proportion of 2-edges that are monochromatic, plus the proportion of
-edges, with the property that the proportion of 2-edges that are monochromatic, plus the proportion of 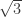 -edges that are monochromatic, are forced to sum to less than 2/3 in any 4-coloring of G, then we are done.
-edges that are monochromatic, are forced to sum to less than 2/3 in any 4-coloring of G, then we are done.
Terry: first I just want to say that this new probabilistic approach seems to be fabulously powerful and I am really excited to see how far it takes us. But I have a question. I’m probably missing something painfully obvious, but as far as I’ve been able to understand it does not, in the general case, provide an explicit construction of a non-4-colorable graph from copies of the graph with the useful probabilistic property. Does it in fact do so, by means that I have failed to grasp? And if not, can it be extended to do so? I’d be particularly interested in the specific example of Lemma 15.
Yeah, converting a proof by contradiction using the probabilistic approach into a finite non-4-colorable graph is actually rather subtle; the “heavy lifting” is hidden by the (not entirely trivial) assertion that the group of Euclidean isometries of the plane is amenable. (Interestingly, this assertion is false in three and higher dimensions – closely related to the Banach-Tarski paradox – so the probabilistic method actually runs into a real problem in high dimensions!)
To actually make the finite 4-colorable graphs, one has to do a _lot_ of spindling and and clamping. It’s a bit complicated for Lemma 15, so let me do a simpler situation with Lemma 2. Suppose we have managed to find a graph G with three long edges, say each of length d, with the property that any 4-coloring of G must make two of these long edges monochromatic. If it was just one long edge that was always forced to be monochromatic, we could spindle G around that edge and get a non-4-colorable graph. But instead we have to spindle G around all three edges at once… but this then creates several more long edges that themselves need to be spindled, and so on and so forth. If one repeats this process a huge number of times, one eventually ends up with an enormous graph that is built from N copies of G for some large N; if N is large enough, we can have the property that (say) 99% of the long edges belong to isosceles triangles. (The fact that we have 99% here has to do with amenability, and something called a “Folner sequence”.) On the one hand, since for each copy of
isosceles triangles. (The fact that we have 99% here has to do with amenability, and something called a “Folner sequence”.) On the one hand, since for each copy of  , at least 2/3 of the long edges are monochromatic, the total proportion of monochromatic long edges is at least 2/3; on the other hand, since each isosceles triangle has at most one monochromatic edge, the total proportion of long edges is at most something like 51%, This gives the contradiction.
, at least 2/3 of the long edges are monochromatic, the total proportion of monochromatic long edges is at least 2/3; on the other hand, since each isosceles triangle has at most one monochromatic edge, the total proportion of long edges is at most something like 51%, This gives the contradiction.
Many thanks! I am visualising this in a manner that does not involve any group theory; can you please say whether it is a valid version of what you are saying?
My visualisation is as follows; like you I am sticking to Lemma 2 for this and applying it to a G of the form you describe. By spindling all three vertex pairs of length d, we are adding three more copies of G, in each of which only one such vertex pair is spindled. But then if we do it again on those three, we are adding six more, and of the total of ten G’s, only six are incompletely spindled, so the proportion of the vertex pairs of length d that are mono is more tightly constrained than before. As we grow this structure (which in chemistry would be called a dendrimer) by repeating this process, the property you describe arises because we are progressively decreasing the surface-to-volume ratio of the thing. The graph that finally crosses the relevant probabilistic boundary may be very much larger than “necessary”, but it will still be finite. Of course in particuar cases we may end up with coincident vertices here and there, but we don’t need to consider that until we actually have our graph.
I am already wondering what we might be able to do along these lines in pursuit of a 6-chromatic graph – and I bet I’m not the only one!
Yes, this is basically what is going on. So the probabilistic method can result in more elegant arguments at the expense of massively exploding the size of the final non-four-colourable graph that one would get at the end of the day, because it’s really an argument coming from asymptotic analysis rather than finite combinatorics. (But the use of asymptotic limits to attack finite combinatorial problems is a well established technique; in my areas of mathematics it is exemplified by the “Furstenberg correspondence principle”, which is actually rather close to the reduction here of the combinatorial problem to the probabilistic one, as is the more recent theory of “graph limits”. And of course the probabilistic method of Erdos is also a basic tool in modern combinatorics.)
Great. Can the non-translatability to higher dimensions be explained in similar terms? I’m having trouble seeing how it works, given that (for example) the spindling argument does seem to translate.
I second the question about the problems in higher dimensions, not sure how it works but would definitely like to know, hoping that there’s some good food for thought there.
Very similar arguments can be found at the end of this paper: https://www.sciencedirect.com/science/article/pii/S0012365X00004064 (calculations with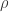 ).
).
The basic problem in higher dimensions is that rotations stop commuting with each other: if one rotates around one axis A and then around another axis B, that’s not the same as rotating around B first and then A. Because of this, spindling (or some higher dimensional analogue thereof) around one edge and then another may produce a different copy of the graph than if one spindled in the other order. Because of this, the number of graphs one uses here grows exponentially rather than polynomially, and one never gets to “outrun” the boundary, there will always be a large proportion of edges that are not properly covered by isosceles triangles or whatever else one is trying to use.
Many thanks Terry. Hm, but I don’t get it. I certainly see that rotations around a sequence of axes doesn’t commute, but surely here we will be rotating around a sequence not of axes but of points, just as in two dimensions? In other words, not really like Banach-Tarski. I mean, yes rotation around a point in a particular direction in R^3 (or above) is also rotation around an axis, but surely it won’t matter what axis, i.e. what particular direction? At the end of the day it’s just the graph itself that needs to have a diminishing proportion of un-clamped edges, no?
I guess for ordinary spindling (basically, using Lemma 2) one may still be OK, but the problem may arise when trying to use a more sophisticated bound such as the one from Lemma 15. It may be possible to still keep the growth of edges polynomial rather than exponential by carefully choosing how one rotates and arranges all the copies of the various graphs, though. I guess one could pretend for sake of argument that the probabilistic methods work in higher dimensions, and only worry about justifying this in case we ever get them to yield a new bound. Probably once we have a working argument using probabilistic techniques, there will be some ad hoc way to extract a more traditional argument based on finite graphs, without having to resort to really large Folner sequences etc..
I see. So generalizing the process well enough may allow this to work in higher dimensions. But the rotations certainly make this unfeasible, and probably puts it far beyond the realm of computability (both from a human and a machine perspective) once we’d get to a high enough dimension. I likely couldn’t even wrap my head around 3D, and much less 8D or 24D…
One of the question in the original post is as follows: In the ring![\mathbb{Z}[\omega_1, \omega_3]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Comega_1%2C+%5Comega_3%5D+&bg=ffffff&fg=303030&s=0&c=20201002) (including complex conjugates), are all numbers of unit modulus of the form
(including complex conjugates), are all numbers of unit modulus of the form  ?
?
Surprisingly the answer is no. The number is a number in the ring of unit modulus that is not of this form. This means that if you combine enough Moser spindles and hexagons you will find some extra unit length edges in the graph that are not part of the Cayley graph for the original generators.
is a number in the ring of unit modulus that is not of this form. This means that if you combine enough Moser spindles and hexagons you will find some extra unit length edges in the graph that are not part of the Cayley graph for the original generators.
I doubt this helps much with chromatic numbers but it is important to know this when looking for homomorphic colourings for the whole ring.
Nice! How did you find this?
Also, do you have an expression in terms of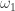 and
and 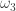 (or
(or 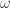 and
and  )?
)?
I was trying to work out systematically the unit lengths and arrived at this one. Here is how to get an expression for it in the ring,
It would require some large graphs to find this hidden link.
This could potentially throw into doubt even the claim that the ring is 4-colourable, but my computations so far suggest that it still is.
I will continue and can hopefully see if there are any more.
On further checking I found that It doesn’t look like it would work out to such small numbers, but it does.
It doesn’t look like it would work out to such small numbers, but it does.
I now have a proof that the elements of unit modulus in the Moser spindle ring are of the form . This is an answer to the second question in this post. I wrote it up as a PDF to avoid the inevitable LaTeX errors.
. This is an answer to the second question in this post. I wrote it up as a PDF to avoid the inevitable LaTeX errors.
https://www.researchgate.net/publication/324950826_Elements_of_the_Moser_Spindle_Ring
The unit-distance graphs on up to 7 vertices can be characterized by 6 forbidden subgraphs. Two should be familiar: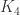 and
and 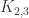 . The others can be found here:
. The others can be found here:
Click to access n7UDgraphs.pdf
This results in 222 non-isomorphic unit-distance graphs on 7 vertices; explicit embeddings are given here:
http://www.hansparshall.com/txt/n7UDcoordinates.txt
These were generated with SAGE, and I’m reporting each graph as a list of its edges. The coordinates were obtained by considering as in the blog post above and the set
as in the blog post above and the set 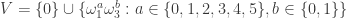 , which amounts to a “spindled hex”. Then each of the 222 unit-distance graphs on 7 vertices embed in the sumset
, which amounts to a “spindled hex”. Then each of the 222 unit-distance graphs on 7 vertices embed in the sumset 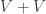 via the explicit embeddings provided above (this is how I found them).
via the explicit embeddings provided above (this is how I found them).
One consequence is a verification that the Moser spindle is the unique unit-distance graph on 7 vertices with chromatic number 4. It is not much work to additionally verify that every unit-distance graph on 8 vertices with chromatic number 4 contains the Moser spindle as a subgraph.
I will update the relevant OEIS entry:
https://oeis.org/A059103
and I intend to try something similar for 8 vertices, where there seem to be roughly 1300 unit-distance graphs. A vast majority of these continue to embed in .
.
In a previous thread, Phillip Gibbs asked if there were 4-colorings of the Moser ring R which is not periodic modulo 4R. The point of this comment is to point out that there are many 8R-periodic 4-colorings which are not 4-periodic.
The ring R is the subring of consisting of elements which are integral over
consisting of elements which are integral over ![\mathbb{Z}[1/3]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B1%2F3%5D&bg=ffffff&fg=303030&s=0&c=20201002) . Phillip Gibbs gave an explicit description of this as elements of the form
. Phillip Gibbs gave an explicit description of this as elements of the form  where a, b, c and d obey certain conditions modulo 4.
where a, b, c and d obey certain conditions modulo 4.
Let S be the subring![\mathbb{Z}[(1+\sqrt{33})/2]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%281%2B%5Csqrt%7B33%7D%29%2F2%5D&bg=ffffff&fg=303030&s=0&c=20201002) . So the norm map
. So the norm map 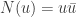 takes R to S. We want to color R such that elements which differ by an element u with N(u)=1 have different colors.
takes R to S. We want to color R such that elements which differ by an element u with N(u)=1 have different colors.
For any k, we have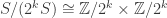 . (Notice that
. (Notice that 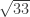 exists 2-adically, so we can send
exists 2-adically, so we can send 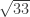 to one of its two 2-adic values.) We then similarly have
to one of its two 2-adic values.) We then similarly have ![R/(2^k R) \cong \mathbb{Z}[\omega]/2^k \times \mathbb{Z}[\omega]/2^k](https://s0.wp.com/latex.php?latex=R%2F%282%5Ek+R%29+%5Ccong+%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F2%5Ek+%5Ctimes+%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F2%5Ek&bg=ffffff&fg=303030&s=0&c=20201002) where
where ![\mathbb{Z}[\omega]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Comega%5D&bg=ffffff&fg=303030&s=0&c=20201002) is a primitive 6-th root of unity. Note that we can extend the norm map to
is a primitive 6-th root of unity. Note that we can extend the norm map to ![N : \mathbb{Z}[\omega]/2^k \to \mathbb{Z}/2^k](https://s0.wp.com/latex.php?latex=N+%3A+%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F2%5Ek+%5Cto+%5Cmathbb%7BZ%7D%2F2%5Ek&bg=ffffff&fg=303030&s=0&c=20201002) .
.
Our coloring will use one of the two projections of R onto![\mathbb{Z}[\omega]/8](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F8&bg=ffffff&fg=303030&s=0&c=20201002) . The elements in
. The elements in ![\mathbb{Z}[\omega]/8](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F8&bg=ffffff&fg=303030&s=0&c=20201002) of norm 1 are
of norm 1 are  ,
,  ,
,  ,
,  ,
,  and
and 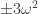 . So (regardless of the comments above about not being sure if we’ve found all the units in R), our goal is to color
. So (regardless of the comments above about not being sure if we’ve found all the units in R), our goal is to color ![\mathbb{Z}[\omega]/8](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F8&bg=ffffff&fg=303030&s=0&c=20201002) so that elements which differ by
so that elements which differ by  ,
,  ,
,  ,
,  ,
,  and
and 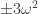 get different colors, and such that the coloring does NOT descend modulo 4.
get different colors, and such that the coloring does NOT descend modulo 4.
Here is the coloring. Our colors are taken from![\mathbb{Z}[\omega]/2](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F2&bg=ffffff&fg=303030&s=0&c=20201002) , also known as the field of order 4. To color
, also known as the field of order 4. To color 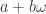 , if
, if 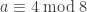 , then use the color
, then use the color 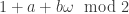 ; otherwise, use
; otherwise, use  . I found this by using Mathematica’s MinimumVertexColoring command and then looking at the output manually. I would guess there are many other solutions as well.
. I found this by using Mathematica’s MinimumVertexColoring command and then looking at the output manually. I would guess there are many other solutions as well.
Yes you are right. There are 4-colourings that are not homomorphic. I can get such mappings for example by just using the numbers a and d mod 8 to define the mapping (for fixed k). I am not sure if that is equivalent to what you are doing. It still works out that 8/3 has the same colour as 0 but not 4/3.
I was looking at this again to put it in the wiki, but I realised there are some other elements of![\mathbb{Z}[\omega]/8](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F8+&bg=ffffff&fg=303030&s=0&c=20201002) which have norm 1. They are
which have norm 1. They are  and
and 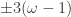 . This reopens the question of whether there are any non-linear 4-colourings.
. This reopens the question of whether there are any non-linear 4-colourings.
The analysis and computer search by Tamás Hubai confirms that these non-linear colorings do exist, and that all colorings have a period of 8
I was wondering if someone could compute the following quantity, concerning Aubrey’s 15-vertex graph U, which has six Moser spindles and hence six edges of length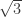 . Given any 4-coloring of U, one can compute the number of these six
. Given any 4-coloring of U, one can compute the number of these six 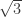 -edges that are monochromatic. I am wondering what the least possible value of this number is. I suspect that it is 2, i.e., every 4-coloring of U contains at least two spindles that are monochromatic at the far ends. This would give the strong-looking bound
-edges that are monochromatic. I am wondering what the least possible value of this number is. I suspect that it is 2, i.e., every 4-coloring of U contains at least two spindles that are monochromatic at the far ends. This would give the strong-looking bound 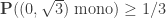 (currently the best lower bound I can get for this quantity is 1/4, see Corollary 16, and the best upper bound is 1/2).
(currently the best lower bound I can get for this quantity is 1/4, see Corollary 16, and the best upper bound is 1/2).
Terry: I haven’t checked whether you’re correct, but if so then this sounds like a terrific first step towards formalising the concept that led me to my solution, as described at the start of section 4 of my paper: uniformity versus lumpiness of the distribution of mono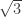 vertex pairs. Accordingly, if indeed all 4-colourings of U have at least two of those pairs mono, it would be very interesting to see if your lower bound of 1/3 can be further improved by examining larger graphs with higher spindle density. The smallest 5-chromatic graphs I found have far less than the maximum possible spindle density for their order, but in this new line of attack we are not seeking small graphs, only comprehensible ones, so that’s not necessarily a disincentive. To give a sense of this, it’s not hard to build graphs with ~1000 vertices and ~3000 spindles.
vertex pairs. Accordingly, if indeed all 4-colourings of U have at least two of those pairs mono, it would be very interesting to see if your lower bound of 1/3 can be further improved by examining larger graphs with higher spindle density. The smallest 5-chromatic graphs I found have far less than the maximum possible spindle density for their order, but in this new line of attack we are not seeking small graphs, only comprehensible ones, so that’s not necessarily a disincentive. To give a sense of this, it’s not hard to build graphs with ~1000 vertices and ~3000 spindles.
Assuming I’m not misunderstanding, I believe the answer is 0. See https://imgur.com/5X7Dx1K. Also, doesn’t it only have 3 Moser spindles, each with two long edges?
Yeah, this seems correct!
Ah well, I guess I was too optimistic (and yes, there are only three spindles; I was thinking of the six rhombi that make up those spindles, and used the wrong terminology). Though it seems that for this particular coloring, while the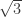 -edges are bichromatic, there are a lot of monochromatic edges at the long side of the narrow skinny rhombi (I don’t know the length of these rhombi offhand, call it
-edges are bichromatic, there are a lot of monochromatic edges at the long side of the narrow skinny rhombi (I don’t know the length of these rhombi offhand, call it 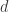 for now). So while one doesn’t get a non-trivial bound purely on
for now). So while one doesn’t get a non-trivial bound purely on  , one might still get a non-trivial bound on some combination of this quantity and
, one might still get a non-trivial bound on some combination of this quantity and  , in the spirit of Lemma 15 in the wiki, if one can enumerate all the colorings of the graph and compute statistics. (More generally, whenever one has an interesting smallish graph, one can try to enumerate all its colorings, and collect various statistics (e.g. number of monochromatic edges of length d). The expected statistics of the random colorings must then lie in the convex hull of the statistics of all deterministic colorings, which can lead to new inequalities on various probabilities as in the wiki page.)
, in the spirit of Lemma 15 in the wiki, if one can enumerate all the colorings of the graph and compute statistics. (More generally, whenever one has an interesting smallish graph, one can try to enumerate all its colorings, and collect various statistics (e.g. number of monochromatic edges of length d). The expected statistics of the random colorings must then lie in the convex hull of the statistics of all deterministic colorings, which can lead to new inequalities on various probabilities as in the wiki page.)
Actually the distance that looks most interesting in that colouring of U is surely , no? – all 12 pairs at that distance are mono.
, no? – all 12 pairs at that distance are mono.
As for your more general idea, would it make sense (in the Lemma 15 style) to seek pairs of distancecs d1, d2 for which the proportions that are mono have a highly inverse correlation? I think the hardest challenge is how to identify which smallish graphs are interesting.
I think Aubrey is right that it’s a matter of finding which graphs are good–I think U isn’t great, because this graph: https://imgur.com/RkIJ6b7 makes none of the edges of length or the d length Terry mentions monochromatic. There might be a better length, though–maybe
or the d length Terry mentions monochromatic. There might be a better length, though–maybe 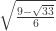 ?
?
Yeah, I guess U wasn’t the best candidate after all, it was just the smallest graph (after things like H, which I think we have squeezed dry of all potential inequalities) that looked like it had some promise. In general, graphs that have an unusually small number of inequivalent 4-colorings would be promising candidates, as they are more likely to have non-trivial restrictions on the total number of monochromatic edges of various lengths.
I think that the probabilistic approach could be potentially a useful tool to prove that P((0,d) mono) -> 1, as d -> 0 and from this deduce that the colors can be supposed to form regions bounded by Jordan curves – in this case it is known that six colors are required.
I’d love to understand that more clearly, I guess I have some studying on such probabilistic approaches to do. That’d be yet another strong hint to the necessity of using regions bounded by Jordan curves and n-manifolds as I have explored from different perspectives already, asides from the issue with neighborhoods from a topological perspective and the issue with measures when optimizing for intersecting exclusion zones.
As far as I know, from there a jump to a lattice-sublattice scheme would suffice for the plane, but there might be more to come in higher dimensions, especially once sphere packing becomes relevant to analyze.
I’ve added a table to the “probabilistic formulation” wiki page listing the distances for which upper and/or lower bounds have been shown, since these seem likely to be the most versatile of the correlations being identified. The format rather betrays my inexperience of editing such pages; everyone please feel free to improve it.
Looks good! I added to the table a bit. I was wondering if you could clarify the comment “Consider the opposite ends of a double triangle and permutations of colours to obtain the exact value 1/2” for the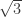 distance? For the double triangle some colorings make the
distance? For the double triangle some colorings make the 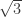 edge monochromatic and some make it bichromatic, but I wasn’t able to draw a non-trivial conclusion for this.
edge monochromatic and some make it bichromatic, but I wasn’t able to draw a non-trivial conclusion for this.
Um – I didn’t write such a comment and I also can’t find it on the page!
OK I see it now – the History page identifies Domotor as the author of that note. Domotor, can you elaborate?
Ah sorry, no, it was Nazgand. Nazgand?
Terry: while we’re clarifying, could you spell out a little more how you got the “slightly nontrivial upper bounds” at the very bottom of the page? Is there a generalisation there (e.g. an upper bound of 1-d, or similar)?
Ah, I see now what you mean by “iterating” i that last comment – you mean that if d>=1/4 then >=1/2 so we can put two small isosceles triangles on the equal sides of the one with third edge 1. So we have 1-a as I guessed, but stepping at powers of 1/2 rather than true at all lvaues.
>=1/2 so we can put two small isosceles triangles on the equal sides of the one with third edge 1. So we have 1-a as I guessed, but stepping at powers of 1/2 rather than true at all lvaues.
So… would I be correct in saying that rather than iterating, we can more simply say that Lemma 17 generalises from triangles to all polygons, and thus that p((0,d) mono = 1/n ?
I am also still intrigued by Domotor’s comment that he suspects the LOWER bound may similarly rise asymptotically to 1 as d tends to 0. Domotor, please elaborate!
@ag24ag24 Yes, I also think that P((0,d) mono)=1/n – just take a polygonal line with n segments of length d connecting two ends of a unit segment.
As for the lower bound for small d – it is a wish, I don’t see any proof how it could be done. That’s why I’ve tried to find lower bounds (see the unit sided regular pentagon on the wiki page).
The =1/n should be =1/n – just like in your comment (I guess).
Thanks. Yes, that’s exactly what I meant by generalising the triangle in Lemma 17 to an arbitrary n-gon. So we can say (abbreviating Terry’s notation for this class of cases) that if a,a…a,b are the lengths of a n-gon, P(a)*(n-1) <= P(b)+n-1. That means we can do a bit better than 1-1/n by using as our b instead of 1, and appealing toTerry's finding that that distance has an upper bound of 1/3. So for example
as our b instead of 1, and appealing toTerry's finding that that distance has an upper bound of 1/3. So for example  <= 2/3 even though
<= 2/3 even though  < 1/3. I will try to cover the full generality in the table.
< 1/3. I will try to cover the full generality in the table.
A corollary is that it would be quite valuable to find a graph all of whose 4-colourings give three specific vertices different colours and in which all distances between those vertices are <1 (and not necessarily equal). The closer those vertices are, the better our upper bounds for all small d become, because the upper bound of the radius of the circle on which they lie becomes 1/3 and so on. I wonder if any of us has looked for such triples?
I think you want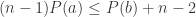 for the
for the 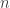 -gon (or
-gon (or  for the
for the  -gon), in which case I think one gets
-gon), in which case I think one gets  for
for  (rather than
(rather than 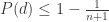 ).
).
Yeah, I corrected it only ten minutes ago, probably while you were writing that 🙂
@domotorp – am I right in saying that your pentagon argument gives 1/5 <= P <= 2/5 for both phi – 1/2 and phi + 1/2 depending whether you draw the pentagon as convex or as a star? I was about to edit the wiki but I want to be sure I have not goofed.
I meant phi and phi-1 of course.
@ag24ag24 Yes, I just was trying to get some lower bound for a small distance but this also works for phi.
@ag24ag24 In https://dustingmixon.wordpress.com/2018/05/01/polymath16-third-thread-is-6-chromatic-within-reach/#comment-4252, it is not entirely true that small distance implies small radius of enclosing circle, e.g., if the distances are d, d, 2d. Could you also elaborate on how this would lead to upper bounds?
Yeah, that was not an intelligent edit on my part.
@domotorp – the reasoning is just that any forced-trichromatic triangle can substitute for the unit triangle in Terry’s Lemma 12 (k=1case), giving an upper bound of 1/3 for the radius d of the circle on which all the triangle’s vertices lie; then if d < we can improve upper bounds for smaller distances by using d as the distance c in (my generalised version of) Lemma 17.
we can improve upper bounds for smaller distances by using d as the distance c in (my generalised version of) Lemma 17.
I’ve never worked with only finitely additive measures, but shouldn’t it be true that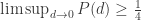 by just taking some random pairs of points?
by just taking some random pairs of points?
I thought conditional probabilities may be useful, so I found some bounds with H.
@Dustin I would like to repeat my feature-request so that you change the theme of the blog such that if I click on a comment in the comment-roll, then it changes color (like from blue to purple). It would be much easier for me (and I suppose others too) to keep up with what I’ve read already.
I’ve looked into it, and it appears that this sort of change would require access to css files that I don’t have with my current WordPress account.