This is the ninth “research” thread of the Polymath16 project to make progress on the Hadwiger–Nelson problem, continuing this post. This project is a follow-up to Aubrey de Grey’s breakthrough result that the chromatic number of the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki page.
Here’s a brief summary of the progress made in the previous thread:
– We now have a laundry list of necessary conditions for a certain family of tile-based 6-colorings of the plane.
The next step is to search for a 6-coloring of the plane. The basic idea is to build up colored plane graphs and prune with our necessary conditions. We were hoping that existing code to generate plane graphs (namely, plantri) could be used as a blackbox for this search, but after further inspection, it seems that we’ll have to write this code ourselves. (When building up plane graphs, we will be adding vertices to the outer face, whereas plantri treats all faces equally.)

Here is a spreadsheet of tiles for 6-colourings. Rules 1,2,4 and 7 have been used to remove tiles while for rule 3,5,6 and 8 are shown where failed. Different colour variants for each tile are given. If you don’t care about those just use variant 0.
I will add more to this as we proceed.
http://phillgibbs.uk/out1.csv
That link doesn’t work – ah, it has a supernumerary “l”
oops http://philgibbs.uk/out1.csv
Looks like you’re missing the “good” entries for variants >0
That was intentional. I was just trying to make it easier to select a list of valid tiles without worrying about the colour variants. In fact for the next version I may just give the number of variants instead of listing them unless you can see a use for them.
List them, but all in the same cell (like the v,v constraints) rather than with separate rows. Can you explain what the numbers in that colours column mean? Also it would be great to use a more immediately intelligible notation for the v,e constraints – maybe a list of v,1v2,v3 where v2v3 is the edge? Then that could also be just one column with >=0 entries per cell.
For the colouring it is assumed that the central tile is coloured with colour 5 and the tile joining edge i starting at zero is coloured with colour i. The numbers then give the colours for the tiles joining at a vertex only, listed in clockwise order.
I will implement your suggestions.
Here is an updated spreadsheet
http://philgibbs.uk/out2.csv
I also added a symmetry column which is “S” for reflection symmetry and “L”/”R” for left/right pairs
Very nice! So I’m seeing a total of 354 good tiles, after deduplicating chiral pairs (i.e. deleting the ones labelled “L”). It will be very exciting to see how many of them can be eliminated in the next step, i.e. when the neighbouring tiles are required to be taken from the set rather than just being well-behaved in the vicinity of the central tile.
I will start to look at that next, but will take it in small steps. There might be a lot to be learnt from joining tiles together two at a time to begin with. That was what I found when doing it by hand with the small set of tiles.
Just as we found rules for validity of tiles we can think of rules that determine when two edges of two tiles can be joined. An edge is determined firstly by the valency of its two vertices. When two edges come together to join two tiles theses valencies must match in reverse. Also, if there is a vertex-edge constraint on one there cannot be one on the other.
Since we are looking at all possible combinations of vertex-vertex constraints and are not assuming that the constraints are being used by the colouring we can assume that if a diagonal or edge is not a vertex-vertex constraint then its length is strictly less than one. This means a constrained edge must match with a constrained edge and an unconstrained edge must match an unconstrained edge. (Here I mean a constraint between the two vertices of the edge, not a constraint between the edge and another vertex)
Apart from those matching conditions there are more complex ones that are required to avoid colouring inconsistencies, and possibly other geometric inconsistencies involving the angles at the vertices etc.
I think colouring variants found for each tile can be efficiently compared for consistency whenever two (or more) tiles are brought together, so it is just any other geometric rules that would be useful to know.
I did not understand the proof of the claim “we can now 6-color [0,2]xR.”
You are probably right, I just do not know what the proof is. It was hyperlinked to some inadequate gibberish. It seemed like a brute-force pixel coloring ought to
work to solve this to pretty good accuracy of the maximum strip-width…
Here is another question: What is the largest radius of a 3 dimensional ball,
such that its surface can be k-colored (for example k-6)? Use geodesic distance.
E.g. if we use the (radial projection of) a regular dodecahedron, then if we scale so the diagonal of a face is 1-epsilon, we can 6-color the 12 faces. Each face same color
as its antipode.
P. Erdos, D. Hickerson, and J. Pach: A problem of Leo Moser about repeated distances on the sphere, Amer. Math. Monthly 96 (1989) 569-575.
showed that on a sphere of circumference 4 one could place N points
so their unit geodesic-distance graph had order N^(4/3) edges
and indeed each vertex had valency of order N^(1/3).
Despite the high valencies their graph in general actually is bipartite (2-colorable),
although it is always possible (via a preliminary projective transformation, which if I am counting correctly has 5 controllable degrees of freedom…)
to force up to 5 “extra edges” each causing 3-cycles.
It seems to me that the sphere is interesting in the following sense.
Some graphs, such as the Moser spindle, still work fine on
any sphere of large enough radius. Call them “generically valid.”
Other graphs, like perhaps de Grey’s, perhaps depend on special
miracles only valid on the exactly-flat plane, and do not work if
any amount of constant curvature, no matter how small, is added.
Similarly the Erdos/Hickerson/Pach graphs are not genericlally valid; they only
work for the very special sphere-circumference value 4.
“Generically valid” graphs remain embeddable on the sphere no matter
if the sphere’s radius is continuously varied (within some radius-interval
of positive width).
Which of the graphs you all have been assiduously producing, are generically
valid?
The tiling of the surface of a sphere has indeed been discussed in the literature – I mentioned it here:
where I note that the sphere of circumference 4 is special in that regard too. A few months ago I thought I had found a gorgeous 36-tile 6-colour covering of a sphere of circumference just over 8 – it was sooo neat… but unfortunately one of the types of tile turned out to have a geodesic diameter of 1.1 or so. So it remains the case that the only known cases in which more than one tile is the same colour are the octahedron on a sphere of circumference exactly 4 and the dodecahedron of circumference in the obvious range.
I agree, the generic-ness of a finite graph to non-Euclidean geometries seems interesting. I guess the hyperbolic case is just as interesting as the spherical case. I don’t know of any work in this area.
Actually the strip was not meant to be a new record width. We already had a strip of width 3.7 in thread 7. This one was interesting because it was five tiles wide in the grid representation we were using, but its physical width is less than the four tile wide strip.
The 12 vertices of the icosahedron on a sphere, or if
we identify each point with its antipode so we are speaking of “elliptic”
nonEuclidean geometry rather than “spherical” — form a set of
6 “equiangular lines” thru the sphere-center.
Therefore, the elliptic nonEuclidean plane, with unit distance
being the length of an icosahedron edge, requires at least 6 colors.
This is a nongeneric result of course since it depends on this very special distance.
But for what it is worth, it breaks the 6 barrier.
(There is a considerable literature on “equiangular lines” mainly in higher dimensions.)
I have a very naive question regarding the $[0,2]x\mathbb{R}$ strip example,
I have not followed completely the discussion neither have I collected all the relevant conditions needed, sorry for that.
But I wonder and would like to ask simply out of curiosity,
what happens if one numbers the (o)range, (v)iolet and (g)reen tiles of the strip example top-down
$v1, o1, g, v2, o2,$ and replace them top to down by
$v(v1), o(o1), g(v1), v(o1), o(v1), g(o1), v(v1), o(o1), g(v1), v(o1), o(v1), g(o1), …$
where e.g. $g(v1)$ is a green colored translated (not rotated, not scaled ) version of $v1$.
would this give a larger strip example?
No – your v(v1) and v(o1) are less than 1 apart. Even to get a height of 5 tiles we need the central tile to be “fat” at both top and bottom.
[starting a new reply so as to skip past the more recent topics]
Actually I’m not very optimistic about the incremental approach here. Yes we will be able to eliminate lots of combinations of abutting tiles, but I’m pretty sure that the number of combinaion that we can’t eliminate will still be enough to be combinatorially prohibitive. I thus feel that we will need to go to SAT-solving on a large island.
There are 2,788341 different ways we can ask if two tiles join. Each of these needs some computation to see if the edge characteristics map and if the result can be coloured. There may be something like 10,000 ways that work. As we attempt to build our islands we will have to ask these same questions many times so we can gain a speed-up factor by three of four orders of magnitude just by testing all possible matchings once and making a table. SAT solvers are clever but they probably don’t figure out that kind of optimisation.
Once we know which tiles and edges can be joined the next step would be to look at which tile combinations can be placed round a vertex. There will be a lot of angle constraints that come into play when we do this so again a large factor could be gained by making a list of all possibilities. Hopefully the numbers will still be something that can be stored in a table. A SAT-solver would not automatically understand constraints posed by angles so this is something we will have to investigate.
The third step will be to construct all 1-Uzbek islands. If you launched into a search for these without first caching the results of the first two steps I don’t think it would be possible. I hope this list of all possible 1-Uzbek islands will be small enough to fit in memory but subsequent steps will depend on numbers. If we can store all viable 1-Uzbeks then building larger islands becomes much more tractable.
Yeah, your algorithm looks about as good as can be done. (You mean 2-Uzbek though – tiles surrounded entirely, i.e. including vertex-neighbours, by other tiles – remember that by my definition the ocean itself is the only 0-Uzbek region.) But I’m still not optimistic… there just seem likely to be too many ways to do the high-valency vertices.
The angles aspect is a good point but I think it can also be SATed. We already have (rule 3) that at most one edge of a 3-valent vertex can be 1 (straight-line distance, of course, not length of the possibly curved edge). Analogously, at most valency-2 of a 4- or 5-valent vertex can be 1. Can more than that be said arising from angle issues?
I have been running some preliminary matching and do indeed get very high numbers of matching tiles joined at edges, about 270k pairs, but I have not yet looked at colouring.
My hope is that we are getting large numbers only because we have put a lot of information into a tile. If we ignored vertex-vertex constraints we would have smaller numbers of tiles. However, I hope that the extra information will narrow down the number of possibilities when we fit more of them together so that the numbers of k-Uzbek islands will be smaller for sufficiently large k. If someone used a simpler tile set and ran a SAT solver it could be better or worse depending on when the pay-off for more information comes in.
Any tile vertex has a maximum and minimum angle as determined by its constraints. We can look at angles between lines drawn from vertex to vertex or angles at the vertex which will differ depending on the curvature. In both cases the total angles of these around a vertex has to be 360 degrees, so having a maximum and minimum for each tile vertex provides a consistency check. I think this will severely narrow down the possibilities for arranging tiles around a vertex.
You say there could be too many ways for high valency, but with high valency it is hard to squeeze in the tiles. It could be the low valency tiles that are harder to deal with because they have less constraints. We will see. Intuitive expectations can be wrong.
I think I am going to write some general algorithms for colouring combinations of tiles so I will be investing some time that will make the initial results take longer but progress will speed up after that.
Having said that, if anyone can see another way to go about this I encourage them to try it.
@Dustin: could you elaborate a little more on why plantri won’t work for us? I’m thinking that we don’t necessarily need to think in terms of building up graphs by sequentially adding vertices. instead maybe we could enumerate all essentially distinct graphs with N vertices (N around 30) that can be the dual of the island. Such graphs would have one special vertex (corresponding to the ocean) with arbitrary degree, together with the following other constraints:
– all other vertices have degree between 2 and 5
– there are no uncrossed cycles of order greater than 6
– neighbouring vertices cannot both be of degree 2 (this can probably be strengthened)
– there is at least one vertex at distance 4 from the ocean
If that comes out to a manageable number of graphs then the only remaining step would be to see whether all vertices other than the ocean can be assigned compatibly to members of Philip’s list (noting that the degree of neighbours of the ocean needs to be treated specially, i.e. tiles with more vertices than the degree of those neighbours need to be allowed) , which a question that seems made for SAT. If on the other hand the number of graphs is too great, some Philip-constraints (or near-constraints) could be thrown in earlier, e.g. just ban degree-2 vertices entirely, or ban degree-5 vertices of uncrossed hexagons.
How does that sound? Is plantri suitable for that?
I expect this method of using plantri to fail because there are simply too many planar/plane graphs. https://oeis.org/A005470 and https://oeis.org/A003094 can give a general sense of how fast the number of planar graphs grows.
But of course we have some restrictions on the graphs, like degrees of vertices. I don’t think they’ll help much, using eg https://oeis.org/A000168 as a guide.
So I wanted to use plantri to “grow” graphs where each intermediate stage is known to be colorable according to our constraints. But as best as I can tell, the internals of plantri don’t allow for that in a way that works for us.
(I could be wrong.)
Yeah, some kind of growing seems to be needed.
What do you think about initially using plantri just to enumerate Philip’s next generation, i.e. islands with one completely landlocked tile? Philip noted that he expects it to be tractable to combine such islands to create ones with a doubly-landlocked tile, etc.
Actually on reading the plantri documentation I see there is a -P option that seems to do a lot of what’s needed, i.e. it provides precisely the special “outer face” you mentioned. Since the graphs being generated are triangulations, it probably makes sense to look not for duals of a tiling but instead for graphs that would correspond to a tiling with a vertex added for each tile that is joined to the tile’s vertices. Each vertex corresponding to a tile vertex would then have even degree between 6 and 12, and each vertex corresponding to a tile would have degree between 2 and 5. Since these degree sets are disjooint we can quickly say things like that all pairs of vertices of degree less than 6 must be an even distance apart, and that the degrees of the neighbours of a vertex with degree at least 6 must alternate between small and large. I guess other tricks will be needed in order to keep the computations manageable – maybe there will be mileage in identifying prohibited subgraphs of increasing size.
I have not gone any further with this yet but usually I find it easier to write my onw code than try to massage some prewritten code into doing what I want. Growing general planar graphs is not a difficult programming task. The problem is to find a way of doing this that is going to be efficient enough to work.
If you count our good tiles by numbers of sides and valency alone there are 78 which is already a high number to fix together. We can try to colour graphs made of these such that no tile is joined by an edge to another tile of the same colour and no vertex has two tiles of the same colour. However, there are many solutions to colour this way with six colours so more constraints are needed.
If we add just the edge-vertex constraints then the number of good tiles jumps dramatically to 313. The grid based search could only construct solutions up to 6 by 10 but if we allow any planar graph it could take a lot of computation to reach that size and there may even be solutions.
Adding in the vertex-vertex constraints gives 563 tiles, but imposes more geometric constraints. Will that be better?
It may be useful to classify tiles in the dual graph first so I am going to think about that before starting the coding.
I just went back to the question of iterating on Proposition 36, and I’m wondering if there is a problem with it in its current (un-iterated) form. The construction appears to allow BE to be arbitrarily small if d is in the vicinity of , and yet BE is one of the distances required to be at least 1/2 in the proof. Am I messing up, or is there a variation on the construction for this problematic ranges of values of d?
, and yet BE is one of the distances required to be at least 1/2 in the proof. Am I messing up, or is there a variation on the construction for this problematic ranges of values of d?
Presuming we can fix that: if I understand it, the minimum permissible value of d if we want to iterate infinitely is obtained when we take B,C,D to lie on a circle of radius d such that |BD| = d and |BC| and |CD| = 1. Thus d = , so a hair more than
, so a hair more than 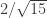 because we can’t still allow BD to go as low as exactly 1/2 – right? At that limit we have |AE| = |DF| = d, |BE| =
because we can’t still allow BD to go as low as exactly 1/2 – right? At that limit we have |AE| = |DF| = d, |BE| = 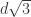 and |BF| = 2d, so everything else is good. I don’t however trust myself to get the last bit right and come up with the correct multiple of delta – I will leave that to Domotor or Terry.
and |BF| = 2d, so everything else is good. I don’t however trust myself to get the last bit right and come up with the correct multiple of delta – I will leave that to Domotor or Terry.
Finally: are there particular values of d (in particular, this minimum value) for which this proof gives a sharper upper bound because additional distances are exactly d?
Hang on… there is a step in the proof that says that AE is monochromatic with probability at most 3 delta. But |AE| = d (whatever the value of d), so AE is monochromatic with probability exactly 1/2 – delta, meaning delta is at least 1/8. Surely I am messing up – where?
Ah, apologies, of course it’s only “outside of epsilon” that AE is monochromatic with probability at most 3δ”.
Concerning my first point, I think I see the issue now: the statements that E and F are the reflections of B and A in AD and DE respectively should actually say that those points are the 180-degree rotations of those points around the midpoints of those lines, such that ABDE and BDFE are parallelograms rather than a kite and a rhombus. In other words, ABFE is a trapezium and D is the midpoint of BF. Now the whole construction makes sense!
Based on this, I think I can shave two of the deltas off. Rather than the trapezium construction, let ABCD be as at the wiki but now let E be actually the reflection of B in AD, and let F be reflection of B in the line perpendicular to AD that bisects it. Then we again have three triangles of sides d, d and the distance required to make BC=CD=1, so the proof can proceed in the same way as on the wiki, except that now every pair of triangles shares the edge AD, so in the last step BF is monochromatic outside of epsilon with probability at most 5δ not 7δ. Thus I think we get p down to 14/29 rather than 15/31, and of course that is before iterating. Please correct me if I’m wrong.
PS – yeah, I see that there is a range of d for which B and F get too close together. Working on that!
Yes, all is exactly as you say! I wonder for which d we get BF=1, that should save even more!
Oops, that d is just what we get from the regular pentagon, for which we already have a better bound… At least this also shows that your improved reasoning works if .
.
At least I got one thing right today 🙂 I think there is another, larger d that also works, where the orientation of BF is reversed.
I am still noodling over further improvements.
Actually I don’t see how you get that the regular pentagon comes in. The values I get for d (after giving up on getting an expression and just evaluating it in Mathematica) that give BF=1 are 1.4413 and 2.5231. However, what I forgot was that we can also have d slightly more than 1/2 and have AB and DF wrap around to the other side of AD; the value I get is 0.566889.
Also there are three values for which BE becomes 1. They seem to be 0.85065 (which may be where you got the regular pentagon thing from), 0.57735 and 0.52573.
A final observation on this topic for now: isn’t your epsilon event overspecified? With your trapezium construction isn’t it enough to use just that at least one of AD and DE is mono? (And in my construction, just AD?)
I’ve been trying to do the iteration thing and I’m getting stuck on an apparent need to assume that p(d) is the largest of the probabilities, i.e. no smaller than p(BD mono) etc. How does one avoid (or guarantee) that?
Urgh, sorry again, I momentarily forgot why epsilon need to have all four length-d edges…
Indeed, I’ve made a mistake, your numbers got to be correct!
Ragarding the iteration – I also got stuck there, that’s why I never wrote up the iteration part… But if we take a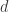 for which
for which 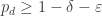 , where
, where  is the supremum, then every other distance’s probability is at most
is the supremum, then every other distance’s probability is at most  larger, and the claim should follow as
larger, and the claim should follow as 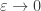 . What do you think?
. What do you think?
I’m not sure… I just don’t have enough practice at this sort of number theory… I’m much better at the geometry aspects! Regarding that, I’m still hunting for constructions that use Terry’s original concept in more economical ways (and/or that avoid having excluded ranges for d).
One thing I’m struggling with is whether there is any way to make useful deductions about the probability that multiple segments are mono, other than building them up segment by segment as in the current writeup. For example, if we take my construction and add a point G so that BEGF is a rectangle, we can say that if the five segments of length d and the four segments like BD are all bi (which gives at most 1/2 + 19*delta) then at least two of the others must be mono, but I can’t get a probability for that. Can you? If so, it seems like it ought to give an improvement.
I’ve been trying to formulate the Prop 36 argument in terms that avoid “event” language, so as to be sure I’m covering all the cases, but I again find myself coming to a much stronger conclusion than is derived there. Please have mercy and enlighten me if I’m just not getting the hang of working with probabilities that don’t obey the normal rules.
Let me work with my new construction from the previous post (though actually I think we can come to the same conclusion with the trapezium). The key insight in Prop 35 is that the probability that AB is mono and AD is bi is at most 2δ, i.e. twice the amount by which p(d) is less than 1/2. So we have p(ABD mono) = p(AB mono and AD mono) >= 1/2 – 3δ because p(AD mono) = 1/2 – δ and p(AD mono and AB bi) = 1/2 – 5δ because p(AD mono) = 1/2 – δ and p(AD mono and AB bi) = p(AD mono and DE bi) = 1/2 – 7δ because p(AD mono) = 1/2 – δ and p(AD mono and AB bi) = p(AD mono and AE bi) = p(AD mono and DF bi) = 1/14 and p(d) <= 3/7, no?
Aargh please ignore that post – angle bracket problem – give me a moment to latexify it…
As I was saying…
I’ve been trying to formulate the Prop 36 argument in terms that avoid “event” language, so as to be sure I’m covering all the cases, but I again find myself coming to a much stronger conclusion than is derived there. Please have mercy and enlighten me if I’m just not getting the hang of working with probabilities that don’t obey the normal rules.
Let me work with my new construction from the previous post (though actually I think we can come to the same conclusion with the trapezium). The key insight in Prop 35 is that the probability that AB is mono and AD is bi is at most 2δ, i.e. twice the amount by which p(d) is less than 1/2. So we have p(ABD mono) = p(AB mono and AD mono)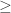 1/2 – 3δ because p(AD mono) = 1/2 – δ and p(AD mono and AB bi)
1/2 – 3δ because p(AD mono) = 1/2 – δ and p(AD mono and AB bi)  2δ. That’s a legitimate way of saying it, right?
2δ. That’s a legitimate way of saying it, right?
If so, then in the same language we obtain p(ABDE mono) = p(AB mono and AD mono and AE mono)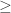 1/2 – 5δ because p(AD mono) = 1/2 – δ and p(AD mono and AB bi) = p(AD mono and DE bi) <
1/2 – 5δ because p(AD mono) = 1/2 – δ and p(AD mono and AB bi) = p(AD mono and DE bi) < 2δ. Right?
2δ. Right?
But then, surely by the same logic we can obtain p(ABDEF mono) = 0 = p(AB mono and AD mono and AE mono and DF mono)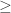 1/2 – 7δ because p(AD mono) = 1/2 – δ and p(AD mono and AB bi) = p(AD mono and AE bi) = p(AD mono and DF bi)
1/2 – 7δ because p(AD mono) = 1/2 – δ and p(AD mono and AB bi) = p(AD mono and AE bi) = p(AD mono and DF bi)  2δ. Thus giving δ
2δ. Thus giving δ 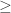 1/14 and p(d)
1/14 and p(d)  3/7, no?
3/7, no?
Aaargh, sorry, I just got confused with my bi’s and mono’s at the end. Ignore that please!
Btw, I’ve just realized that the <1/2 bound for monochromatic distance point pairs implies that for any triangle that has one unit side, and the other two sides are bigger than
distance point pairs implies that for any triangle that has one unit side, and the other two sides are bigger than  , we can find a trichromatic copy of it – with Tamas our main result last year was proving a special case of this with the combinatorial tricks of rotating the hexagonal lattice.
, we can find a trichromatic copy of it – with Tamas our main result last year was proving a special case of this with the combinatorial tricks of rotating the hexagonal lattice.
OK… I have convinced myself that we can actually get to δ = 1/46 (or 1/50 with your trapezium structure that avoids the problematic ranges of d). Given my lack of knowledge of this area I just bludgeoned my way through the algebra from first principles and it seemed to work, as follows.
If we assign their own δ’s to the p(mono) of {BD,DE,AF}, of BE, of BF and of EF – let’s call these p,q,r and s respectively – we derive the strengthened inequality that 29δ is at least 1/2 + 3p + q + r + s. Then δ >= 1/58 as already discussed, and it must be larger than that if any of p,q,r,s are greater than 0. But since we can draw the same structure with the segments that are currently of length d getting the current length of BD (resp. BE,BF,EF), we can say that p,q,r,s are all in fact at least 1/58. Thus, we can in fact say that 29δ is at least 1/2 + (6*(29+6))/(58*29) – and it must be larger than that if any of p,q,r,s are greater than 1/58. Obviously we are now iterating, and by considering the sums of infinite convergent geometric progressions I conclude that (as you suggested at the outset) we successfully converge to the loss of all those six “variant δ’s”, so via my construction we get δ = 1/46 and p(d) upper-bounded at 11/23.
A problem is that this all fails if any of the distances ever goes under 1/2 during the iteration process. If d starts large, like 2, then things are fine if we stick with the trapezium construction, but unfortunately with my construction BF is shorter than d, so we can spiral down into prohibited ranges. Maybe it sometimes gets into convergent spirals that avoid those ranges, but I don’t have the strength to work out the details – the better part of valour is probably to retreat to the trapezium construction, replacing all 29’s above with 31, and accept a p(d) upper bound of 12/25.
Please check my reasoning here and let me know if I have messed up. If it’s OK I will update the wiki.
PS: as noted earlier, this all relies on d being at least so that BD etc are no shorter than d.
so that BD etc are no shorter than d.
For clarity: the statement “29δ is at least 1/2 + (6*(29+6))/(58*29)” is of course two iterations in – I skipped the intermediate “29δ is at least 1/2 + 6/58”.
Finally I’ve managed to catch up with this and entered all the arguments in the wiki under Prop 36 – please let me know if I’ve messed up anything or just simply change it!
Looks good to me! Thanks for such a good formalisation of what my revised placing of F can and cannot deliver.
In other news, the issue of Geombinatorics with my paper is now out. It also features Marijn’s report of the 553-vertex graph and Geoffrey and Dan’s report on graphs excluding two distances, as well as a very nice introductory piece by Soifer.
In more other news, Dan recently told me that he and Geoffrey have extended their two-distance work in wha seems to me to be a very important way: for the additional distance 2, they have achieved chromatic number 6. I know no other details as yet but I am eagerly awaiting them!
@domotorp – I’ve just seen your revision of the lastpart of Lemma 36 – I think it may be fractionally incorrect, because in addition to the three distances of my construction that tend to 2 as d tends to infinity there is also one that tends to 4, and only six that tend to infinity (four that are exactly d and two others). I changed that in the wiki, but I could not convince myself how (if at all) it changes your final calculation, so I leave that to you.
Indeed – thanks, I’ve fixed it!
I think I can get a useful upper bound on p(d) for all d (even less than 1/2) by a suspiciously simple construction. (By which I mean that yeah, I’m probably messing up again… please check the following.)
Let ABC be a unit-edge triangle, and let D be any point such that AD=BD. Let |AD|=|BD|=d and |CD|=e, and pick D such that . Note that
. Note that 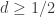 but e can be arbitrarily small. Let
but e can be arbitrarily small. Let 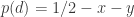 and
and  , where 1/2 – x is the supremum of p over all distances.
, where 1/2 – x is the supremum of p over all distances.
Now trace through the early part of the logic of Prop 35 (or 36), as follows. AD and CD are individually mono with probability 1/2-x-y and 1/2-x-z respectively, but cannot both be mono. Thus, the probability that AD and CD are both bi is at most 2x+y+z. Similarly for the probability that BD and CD are both bi. Next para: if AD is mono, then CD is not mono, and thus BD is mono outside of an event of probability at most 2x+y+z. Putting that in words that I find more natural, the probability that AD is mono and BD is bi is at most 2x+y+z.
But wait – in this construction, p(AD and BD both mono) = 0, so that probability is simply the probability that AD is mono, which is 1/2-x-y. So , i.e.
, i.e.  , i.e.
, i.e. 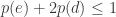 . Since for any distance p there exist locations for D that make d=p and also ones that make e=p, I think this means that the average value of p over all distances is at most 1/3.
. Since for any distance p there exist locations for D that make d=p and also ones that make e=p, I think this means that the average value of p over all distances is at most 1/3.
I’m not quite sure where to go from there. Clearly (if the above is not broken) this gives us new upper bounds on the lengths that d gets when we set e to values for which we already have positive lower bounds; for example I think since that’s d when e=2. But can we say anything more than that?
since that’s d when e=2. But can we say anything more than that?
Sorry for re-use of “p”! I should have said that since for any distance q there exist locations for D that make d=q and also ones that make e=q, I think this means that the average value of p over all distances is at most 1/3.
This is certainly correct, in fact, probably the proof can be shortened significantly to conclude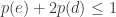 – note that this was used already in the table in the special case
– note that this was used already in the table in the special case  . But it is indeed a useful lemma that combines lower and upper bounds in a non-trivial way.
. But it is indeed a useful lemma that combines lower and upper bounds in a non-trivial way.
Thanks Domotor! I have added this (in substantially abreviated form) to the wiki as Lemma 38; please edit as you see fit.
So the implication is that we would have a human proof that CNP is at least 5 if we could find a human-analysable UD graph and a triple {d,e,f} that can be the distances from a point to the vertices of a unit triangle, such that there is a set of vertex pairs of the graph that includes at least one pair of all three lengths and more than 1/3 of which are mono in any 4-colouring. Do I have that right?
Indeed! Just in your set of vertex pairs, there should be the same number of pairs at distance d, e and f. I suppose that there is a hope that we can also win here some small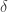 . That would imply that it’s sufficient to find a 5-chromatic graph where all but 3 distances are unit, and these 3 exceptional distances are d, e and f.
. That would imply that it’s sufficient to find a 5-chromatic graph where all but 3 distances are unit, and these 3 exceptional distances are d, e and f.
Ah yes – thanks for that correction. I have just added a note to Lemma 38 recording this. I agree about seeking a delta! – but I don’t yet see a way to do that.
In case anyone was labouring under the misconception that the recent silence here implies inactivity, I am delighted to point everyone (and especially those of you who are not signed up to receive alerts) to today’s awesome contribution by Jaan Parts:
That was a logical place for him to post it, of course, but since that page is six rollovers old I thought it best to bump it to here and to suggest to Jaan (and everyone else) that any new replies should be posted on this page instead. Meanwhile please see also his followups giving links to his constructions, and most notably this one:
https://drive.google.com/file/d/1IG57N11-lRH40Tu-1BDY-8PxWowqAP4s/view
Bravo Jaan! Let’s see if we can’t push this a little further.
Sorry, I have placed my reply on the second thread already. Here is an addition.
I’m happy, that my message was interesting for you. And I have to say: guys, you are really great with your 5-coloring!
I think, the lower bounds, based on pigeonhole principle, are very very weak and have no practical meaning. The expected exact bound for 4 colors is some hundreds, the pigeonhole bound is only 12. For 5 colors the pigeonhole bound is now 24, the true bound will be (I think) many thousands. For 6 colors the pigeonhole bound is about 7000, the expected exact bound will count millions.
Maybe it is better than nothing. And a little better than it was. For me it is the kind of sport.
Many thanks Jaan. You are quite right, but that is only part of the point. The main motivation for exploring this is that tilings covering nearly all the plane with fewer than seven colours may give us clues towards finding tilings that cover the whole plane with six colours. We are already employing various other techniques to seek such a tiling or to determine that none exists, but this is an additional tool.
Here is a copy of my post about Pritikin’s bound enhancements:
All unit-distance graphs of order N=6906 are 6-colorable.
One can use the following tricks to adjust N: modify the shape of existing diamonds (12-vertex polygon instead of rhombus), introduce some other diamonds, use 15-vertex polygons instead of heptagons for colored tiles, attach round segments to some edges. After optimization of polygon parameters N=6899. After attaching of segments N=6906.
The construction for 6-coloring is shown here:
https://drive.google.com/open?id=1AsOb7GDImtLMjQL0AR-4fFP7uuc37wy8
All holes are increased many times of course. The real coloring is visually just a set of pentagons.
Many thanks Jaan. On studying your description of your method, I see a parameter that you might want to add (for the 5-colour case). I do not see any obvious reason why the period of the tiling should be on an equilateral-triangle grid. in particular I think there is a case for allowing the grid to be stretched/compressed in what is the vertical direction in your diagram. Similarly, there may be something to be gained from allowing “shear”, i.e. from letting the rhombus formed by the centres of four red (resp. purple) tiles be squarer (or less square) than the 60/120/60/120 shape that you are currently enforcing. (I’m not completely sure that these two suggestions are not just two ways of describing the same single additional parameter!)
Thank you, Aubrey, for your suggestions. The grid is not equilateral already and it is described by three parameters (distances between centers of tiles of the same color). Two of them are equal on final design, so it is isosceles. My plans were to vary all three grid parameters, but I think, it will not give some enhancements. I’ll try anyway. Now I’m playing with other designs. Without any progress.
Ah, OK. Yeah, I have also failed to find any other designs that come close.
One other thing you might perhaps try with the existing design is to treat alternate rows independently, i.e. to optimise the coverage of a rectangle that spans four rows (two of them red and purple, two of them yellow/blue/green). That’s what I was half-thinking when I mentioned “shear”. I have a feeling that there is scope for some small improvement from that addition.
Btw, if I understand well, these types of bounds should also hold for graph with a bichromatic origin – so for 4 colors, the 12 is quite close to the optimal 24. (For 5 and 6 colors, I wouldn’t expect the numbers to be near.)
Actually, I’ve realized my proof was wrong – I wonder if some similar statement is true.
To clarify: I didn’t mean that one would just shift an entire row but keep it the same shape as the other row that uses the same colours. The distance between (and indeed the shapes of) the centres of the red and purple tiles in the upper row would not be constrained to be the same as for the lower row; similarly for the yellow/blue/green rows.
I’ve been having another look at the very cool idea explored some time back by Boris, of seeking a 6-tiling of the plane by SAT-solving a grid. As you’ll recall, the roadblock that that approach hit was that the only way to cover more than about a 2×2 area is by using unscaleable tilings with curves as boundaries, which can’t be found by any approach based on stopping pixels that overlap each other’s annulus of exclusion from being the same colour. Peter is (I hope!) still beavering away on an exhaustive search of all such tilings (ignoring, for now, the special category where there are small tiles that lie inside each other’s annulus of exclusion), but in the meantime maybe the grid approach can be enhanced. A while ago I posted an embarrassingly half-baked suggestion for that, but I think I can now do better. Comments please from the SAT experts! (Also, with a bit of luck Boris and I will be able to discuss this 1-1 ten days from now with the added benefit of beer, so any preparation prior to that could have additional value.)
OK, so here is my new suggestion:
– We will work only with gridpoints, not with pixels per se.
– For each gridpoint A, denote its eight neighbours by N_A.
– for any two gridpoints A and B, let p(A,B) be True iff at least 3 of N_A are >1 from B and at least 3 are <1. (Maybe relax this to 2?) Denote the three members of N_A that are closest to B by S(A,B) and the three furthest by T(A,B); reciprocally S(B,A) and T(B,A).
– Allow A and B to be the same colour, X, iff any of the following hold:
– – p(A,B) is False
– – no member of S(A,B) or S(B,A) is colour X
– – no member of T(A,B) or T(B,A) is colour X
How does that sound? I have not yet been able to decide whether the above criteria are ideal – in particular, whether we need to specify that some of the other neighbours are coour X – but I think this is a starting-point that should give the pixellation approach access to unscaleable tilings. Am I missing anything?
Further to this: according to initial experiments it seems to work. First a clarification: in my previous post the criterion for allowing the same colour should have included whether the vertices are equal to, greater than, less than 1. Specifically, we actually allow A and B to be the same colour, X, iff any of the following hold:
– p(A,B) is False
– |AB| is greater than 1 and no member of S(A,B) or S(B,A) is colour X
– |AB| is less than 1 and no member of T(A,B) or T(B,A) is colour X
I’ve implemented this in Mathematica on a standard MacBook Air and the main caveat is that with this non-optimised code (and with such puny hardware) I can only work with really coarse grids. But with that limitation acknowledged, I am essentially finding that a square of edge 3 can be 6-coloured but one of edge 4 cannot. The code generally seems to be behaving as expected, in that the solutions being found are broadly tile-like, though with these coarse grids there are occasions when somehow a fine mesh is allowed – I’m ignoring those.
If this holds up, I think it is worth asking what would be required of such analyses to get us to a proof that tile-based 6-colourings don’t exist. I’m fairly sure that (in contrast to Boris’s original method) my approach is overly permissive, i.e. that it will allow anything that works in a non-pixel world as well as some things that don’t – but I’m not sure I can prove it. Any ideas anyone?
In a very recent joint paper with Geoffrey Exoo we consider the following variation of Hadwiger-Nelson problem.
Let $d\neq 1$. Estimate the number of colors needed to color the plane so that no two points distance $1$ \underline{or} distance $d$ apart are colored the same.
Clearly, at least five colors are needed. Extending the notion of unit-distance graph
we define a $\{1, d\}- graph$ to be a simple graph which allows a plane embedding such that adjacent vertices correspond to pairs of points $1$ or $d$apart.
For several values of $d$ we constructed small 5-chromatic $\{1,d\}$-graphs.
A few days ago we succeeded to construct a 6-chromatic $\{1,2\}$-graph.
Please refer to the file http://cs.indstate.edu/ge/ExooIsmailescuData/vlist301.txt.
which contains a list of 301 vertices. We denote this graph as $G_{301}$..
The coordinates of each vertexof $G_{301}$ are given in the format [a1,a2,a3,a4,b1,b2,b3,b4] which means that the coordinates are
X= (a1+a2*sqrt(3)+a3*sqrt(11)+a4*sqrt(33))/12 and
Y= (b1+b2*sqrt(3)+b3*sqrt(11)+b4*sqrt(33))/12
The graph $G_{301}$ has 1422 unit edges and 678 edges of length 2.
A picture of is available at at http://cs.indstate.edu/ge/ExooIsmailescuData/
$G_{301}$ is 5-chromatic but it has twelve pairs of points each of which is
monochromatic in every 5-coloring.
Numbering vertices from 1 to 301, one such pair is $\{176, 290\}$.
Another one is $\{177,291\}$. All such pairs are distance 5 apart so spindling is possible. While only one such edge would suffice we preferred to have a highly symmetric graph.
One obtains a 6-chromatic {1,2}-graph with no more than 601 vertices.
One way to verify this is as follows:
Consider the subgraph induced by the first 169 vertices in the list.
(a separate list is also available at http://cs.indstate.edu/ge/ExooIsmailescuData/)
This subgraph has 738 unit edges and 306 edges of length 2.
There are exactly 32268 5-colorings of this graph.
The role of the remaining 132 points is to eliminate as many of these colorings as possible. In the end, only 18 of the 32268 5-colorings survive and all these colorings force color(176)=color(290). Spindling finishes the job.
Aubrey informed us that verifying that $G_{301}$ with the extra fake edge {176,290} is 6-chromatic can be accomplished in fewer than 30 seconds by using Mathematica.
Also, there are several different graphs that can be obtained after spindling.
The final graph depends on three factors:
1. which vertex one keeps fixed and which one one rotates,
2. the rotation could be clockwise or counterclockwise
3. the rotated vertex of the spindle is distance 1 or distance 2 from it initial position.
Aubrey noticed that it may happen that in the process of spindling, unexpected vertex coincidences may result, and additional (unplanned) edges may appear. These edges have one endpoint in $G_{301}$ and the other in the rotated copy of $G_{301}$.
Probably significantly smaller $6$-chromatic $\{1,2\}$-graphs exist.
It is unclear to us if this type of result will help us construct a 6-chromatic unit-distance graph but we think it is a step in the right direction.
One obvious line of research is to find other values of $d$ for which
6-chromatic $\{1,d\}$-graphs exist.
.
Many thanks Dan! Yeah, I think there are really good prospects here. In the first instance it would be great if you could give us some info about how you found this graph. Also, I hope that Marijn can apply his cool clause-elimination method to derive smaller ones. Conversely, one could try to identify vertices to add to the graph that would reduce the number of required edges of length 2. (For that matter, how many of those in this graph are actually needed in order to retain 6-chromaticity?)
With Nora Frankl and Tamas Hubai we’ve been intensively working on the bichromatic approach in the past few weeks, and now we came quite close to a human proof, so we thought it’s time to share our ideas. For example, we’ve managed to show that if there is a k-chromatic unit distance graph with a bichromatic origin, such that all its neighbors are in the upper halfplane and all their coordinates are rational, then CNP>=k.
Below I sketch the main ideas.
We tried to follow the path I’ve proposed here, about artificially creating a bichromatic point:
The respective problem for lines instead of unit disks turned out to have a surprisingly elegant solution that Nora found:
https://mathoverflow.net/a/306966/955
Unfortunately, a similar approach doesn’t seem to work for a collection of unit disks C that go through a common point. Here we would need finitely many points S such that if we place the disks C on S, then the locus of the common of the disks is not just finitely many points, but a curve. This seems to be the case only if S is congruent to the centers of C (in which case the curve is a unit disk), as if |S|=|C|=2, the locus is a degree 12 curve with many parameters determined by the points. Finding a congruent S would be equivalent to a trichromatic origin, so even using that the unit distance is forbidden, seems hard.
So instead of finding several possible places for the common point of C, we must be happy if there’s just one. This is the case if S is similar to the centers of C (with a small enough diameter), and luckily we can find such a monochromatic S using Gallai. Then if the common point of C has a different color, we are done, and otherwise we can conclude that we have a larger monochromatic structure. If the structure of C is ‘nice’, then this monochromatic set eventually propagates into an infinite grid. When applying Gallai, we can achieve in fact that the first similar copy we start with is such that the side-length of this grid is the reciprocal of an integer, which means that in the infinite grid we’ll have a unit distance, a contradiction.
So how can we prove that some S will propagate into an infinite grid? This is related to this question (warning: S denotes something else!):
https://mathoverflow.net/questions/300604/almost-monochromatic-point-sets
Suppose that our propagation rule is (A,b) meaning that if there is a monochromatic similar copy of A, then b also has this color (where the same transformation is applied to b as to A). For example, if the points of Z are colored with finitely many colors, and the propagation rule is (A={1,2,3}, b=4), then we can find a monochromatic arithmetic progression of length 3 using Roth, e.g., 12, 22, 32, and conclude that all the subsequent terms in this progression share this color, i.e., 42, 52 etc.
A similar argument works if b is not in the convex hull of A, and there is a ‘nice’ 2-dim grid (like the square-grid, or the triangular grid) that contains A and b. This is because using Gallai we first find a large section of a grid containing a similar copy of A and b that is monochromatic. Then we keep on increasing the radius of the largest disk inside which all grid points are monochromatic the following way. Pick the nearest point of the grid not yet in the disk, and rotate and scale (A,b) so that b is on this point, while the rest of A is inside the disk. Such a transformation of (A,b) always exists if the grid is ‘nice’, which means that there’s a non-trivial linear transformation that maps the grid to itself. (Is there a word for this?) Unfortunately we have some constructions showing that without requiring that b is not in the convex hull of A, or without the ‘niceness’ property, no finite subset of the grid can propagate into an infinite structure, not even to an infinite arithmetic progression. So here we are stuck but maybe someone has an idea how to go on…
Also, as can be seen from the proof, it’s not really needed that all of the neighbors of the bichromatic origin are on the upper halfplane of a nice grid; it’s only that for the rest of its neighbors it will not count as bichromatic. So the origin has a color, red, that forbids any of its neighbors to be red, and for its neighbors that are in the upper halfplane of a nice grid, blue is also forbidden. Tamas found some simple to construct examples (the length 1/7 triangular grid has 18 points on a unit circle (of these 9 are in the top halfplane), he took the Minkowski sum of these with V+V (which is |V|=30 from Aubrey’s paper), and then eliminated some vertices) that have about 1000 vertices, which is still quite a lot, but very likely this number can be reduced significantly, the question is whether enough to get a human-verifiable example.
Splendid! I’m not pretending to follow the whole thing (e.g. I have no idea who Gallai or Roth are or what they did that this relies on) but that wouldn’t stop me from looking for a small graph that fits your criterion. Couple of questions about that:
– are neighbours that lie on the x-axis allowed to be blue?
– at the top you say that the coordinates of the neighbours must be rational, but then at the bottom you talk about a triangular grid. I don’t see how to reconcile these statements. Can you be more explicit about what is and is not a nice grid? – e.g. would any rectangular grid be OK?
Gallai’s theorem says that given a finite planar set of points C, in any coloring of the plane (with finitely many colors) we can find a homothetic (scaled and rotated) copy of C that is monochromatic. The same also holds for the square grid instead of the plane.
When writing Roth, I wanted to use the result that in any coloring of the integers (with finitely many colors) we can find an arithmetic progression of length 3. This is a special case of van der Waerden, and in fact Roth proved something much stronger, instead of colorings about one dense set, which makes it a special case of Szemeredi, so probably I should have referred to my claim rather as van der Waerden.
I now see that the answer to my first question must be “No” because you’re working with ever-larger disks, but I’d love to know why the shape needs to be a disk (or even to be convex). Please feel free to direct me to the Gallai result on which you base this part.
To clarify my second question: I see your statement that a grid is ‘nice’ if there’s a non-trivial linear transformation that maps the grid to itself, but I’m not seeing how that is not vacuous. For, suppose you have a finite graph satisfying your convex-hull criterion but with arbitrary coordinates for the vertices. Then, surely you can draw horizontal and vertical lines through each upper-half-plane neighbour of the origin, and make your infinite grid just as copies of that, translated horizontally and vertically by all integer multiples of the distance between (respectively) the leftmost and rightmost gridlines and the topmost and bottom-most ones? Hence I think I must not be getting what you mean by a non-trivial linear transformation. I’m guessing that this is also something reliant on knowing what Gallai or Roth said.
Also, can I clarify something about your final point? You note that it’s OK for the origin to have neighbours in the lower half-plane, just that they can be blue. I’m guessing those neighbours can also have arbitrary coordinates, not necessarily on grid points – right? And similarly, can there also be additional neighbours of the origin in the upper half-plane that are not on grid points, just that they too are allowed to be blue? If so, I suspect we’re within reach, even if your answer to my “niceness” question is no, the grid has to be nicer than that.
The shape needn’t be a disk, you can also use an argument to extend the monochromatic part to growing squares, just the proof is easiest for disks (intersected by the grid points).
I think that your troubles with the grid are due to my lack of defining them, sorry for that. By grid, I mean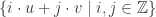 , so the distances among parallel lines of the grid are all equal.
, so the distances among parallel lines of the grid are all equal.
You’re right about the conditions of the origin, it can have any type of neighbors, just that we can use its bichromacity only for the particular set of neighbors in the (open) top halfplane having rational coordinates. So we can use this condition for any unit distance graph found so far by selecting an appropriate set of neighbors, but it seems to me that for these graphs we can’t win more than by simply using that two of its neighbors at distance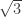 are monochromatic, which we also know from e.g. probabilistic formulation (btw, the polymath wiki is down at the moment).
are monochromatic, which we also know from e.g. probabilistic formulation (btw, the polymath wiki is down at the moment).
Last post for tonight 🙂 I had a quick look at variations on the choice of 1/7 for the triangular grid and I wonder if 1/14 might work better, since 196 is not only 4 + 3*64 but also 169 + 3*9 and 121 + 3*25. If I’m not mistaken, this means you’d have a total of 21 points on the triangular grid to play with that can’t be red or blue, rather than only 9.
Ah… no, those nw diamonds all coincide with the old ones… it did seem a bit too coincidental to be true!
I have added a new probabilistic lower bound (unrelated to my previous comment) that seems to improve one of the (I don’t think important) computer-verified lower bounds:
http://michaelnielsen.org/polymath1/index.php?title=Probabilistic_formulation_of_Hadwiger-Nelson_problem#Lemma_39
More importantly, this seems to be the first lower bound for arbitrary numbers, so it follows, e.g., that if we forbid 1 and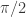 , then the chromatic number is at least 5. This is interesting because it is conjectured that forbidding linearly independent distances cannot increase the chromatic number.
, then the chromatic number is at least 5. This is interesting because it is conjectured that forbidding linearly independent distances cannot increase the chromatic number.
I wasn’t aware of that conjecture – who has discussed it? That would certainly seem to give additional impetus to the idea at the end of Dan’s recent post, of seeking lengths other than 2 whose prohibition delivers something 6-chromatic.
It’s page 21 here + personal communication with the author for the stronger version that I’ve stated above: https://arxiv.org/pdf/math/0703856.pdf
I have been ruminating about 6-chromatic two-distance graphs and have come fairly close to something quite small where the other distance is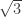 , starting from the observation that a 5-colouring of a unit hexagon in that world necessarily has two mono diagonals. That leads to things mighty reminiscent of the J,K,L logic from my paper, but I have not quite been able to make it work. I thus put it out there in the hope that someone else can spot something I’m missing!
, starting from the observation that a 5-colouring of a unit hexagon in that world necessarily has two mono diagonals. That leads to things mighty reminiscent of the J,K,L logic from my paper, but I have not quite been able to make it work. I thus put it out there in the hope that someone else can spot something I’m missing!
One thing that came up during my excellent meeting with Boris yesterday was that he reminded me of an idea of Philip from May:
Did anyone examine this idea further? I’m thinking that maybe some of our more recent tools can help. In particular I bet we could try some large-but-not-insane subgraphs of Philip’s ones and see how easy they are to colour under his stated criterion.
Here are two examples of tile based plane coloring using only small tiles.
It is possible to place more than one small tile inside of unit diameter circle. It helps to reduce the number of used colors. I think one can use this property as definition for small tiles. Otherwise there is no noticeable difference between small and large tiles. Every separate tile can be called as large one even if it is smaller in size than Pritikin’s diamonds.
In any case the number of colors increases with reduction of tile size. The tessellation can be 8-colorable when unit circle contains 2 tiles (with width less than 1/3, height about 2/3):
https://drive.google.com/open?id=1F3IC8IBuiaW_apzgSBSWQHUB6ZukRFbe
The tessellation can be 9-colorable when unit circle contains 3 tiles:
https://drive.google.com/open?id=1MwPnp5VjXe24GrdO9DOPzL2FD9jX2Tyq
In the last tessellation there is no degrees of freedom for vertices placement. Every tile is a regular hexagon with edge length 1/7.
One can use similar tessellations to try to get 6-coloring (with no success, I think) replacing some of small tiles by large ones.
Some corrections for small tile definition. Of course one can find a lot of circles, that contain only one given tile (or no tiles with given color at all). It is essential that for any small tile there exist some circle, that contains also at least a part of other small tile of the same color.
Been a while since I posted, but I kept working on my preferred subproblems here and there.
I’ve figured out a way to model 3D exclusion zones in an acceptably short amount of time. I’ve used that to take a look at the Weaire–Phelan structure, but even before finishing the process I realized that I see no way of getting it below 15 colors, because the tetradecahedron (14 faces) forms a 15-complete subgraph with the adjacent cells. There’s no trivial fix to this either.
A base cell will always form a complete subgraph with all other adjacent cells, except those that are only adjacent via a single vertex. So if we’re to find a honeycomb with less than 15 colors it’ll have to have 13 or less faces on all cells.
To that end I’ve taken another look at the dual tessellation of the known 15 coloring, the rhombic dodecahedral honeycomb. It has only 12 faces, so going by that alone it might have as little as 13 colors. It does however have 18 adjacent cells, 6 of which are only adjacent through a single vertex. Those 6 cells may only require 3 colors, but that still leaves us with a minimum 16-complete subgraph, even before testing if that pattern is repeatable at all.
We’re seeing the same with Aubrey’s pentagon tesselation. 5 faces, but 7 adjacent tiles. 2 of these tiles are only vertex adjacent, and do not need to share a color. The curved boundaries break two more connections, allowing for the known 7-coloring.
I guess that’s it for my exploration into 3D coloring for the moment, as I’m out of usable honeycombs and ideas. All of the ideas I have left are out of reach for now, such as adapted Voronoi techniques.
So it seems WP has changed its way of embedding pictures. Here goes another attempt:

According to Coulson (“A 15-colouring of 3-space omitting distance one”) any lattice-sublattice coloring scheme for 3-space must use at least 15 colors to have an excluded distance. If I understand it right, any 13- or 14-coloring (if it exists) should have some irregular structure.
Right. I conjecture that, if such a 3D coloring exists, it is based on a regular lattice-sublattice scheme. However on top of that there would have to be unit distance radius arc hypersurfaces, sufficiently reducing the exclusion set sizes of cells to allow for less colors. I never expected the rhombic dedecahedral honeycomb to actually have less than 15 colors but I deemed it a possible candidate for such boundary modification.
And on that front I was correct.
The exclusion set size of these cells is 86. Using curved boundaries we can definitely reduce this number. For example there are these spots (red are the excluded cells except one, green is the exclusion zone of the center cell):

We can see that the missing excluded cell is only excluded through a relatively small volume. We can adapt the other 3 cells to include this volume, bringing the exclusion set size of the center cell down to 85.

Now this new excluded volume very barely touches a few new cells, but we can repeat the process again, this time without excluding new cells.
Now I haven’t bothered figuring out how far the exclusion set size can be dropped and if it’s enough to omit a color because that’d be a huge amount of work for little gain, but that’s the principle and it works.
Now… it may also be the case that the base grid is irregular and we then need these boundary modifications on top. If so these would be extremely complicated constructs.
And considering that sphere packings in some dimensionalities are irregular I suppose such constructs are likely neccessary for the most efficient coloring there. But there’s a lot of work to be done before we can even think about tackling such constructs.
My new comment needs moderation because of WPs 2 links rule.
Did you find the exclusion set size for Coulson’s 3-space tessellation? It is interesting to compare it with your results for the rhombic dedecahedral honeycomb.
I’ve got another question, Bernhard. You have posted the coloring of some tessellation here:
Could you show the coloring of that tessellation for two or three times larger area to see some periodicity? I’m not sure that it is 7-colorable.
The exclusion set size for the bitruncated cubic honeycomb (Coulson, Tóth, Radoičić) is 64, neatly aranged in 2 layers, the inner one of course being 14 and the outer one 50 cells. So it’s a lot less.
I’ve never bothered seriously trying to reduce this number though, for 2 reasons. It’s certainly not possible to reduce the chromatic number any further with this honeycomb due to the 15-complete subgraphs, and from what I remember the exclusion zones have always cut relatively deep into the cells of the second layer, making it accordingly difficult or impossible to gain anything from such modification.
As for that mix tesselation, I remember that coloring it back then was unexpectedly tricky, because there’s a lot of room for moving colors around and no immediate clear emerging guidelines. Manually expanding it is complicated for that exact reason.
I’ll see about feeding it into SAGE but that’ll take me a while.
I mean… I guess there’s a faint chance for it to not be 7-chromatic, but I’m relatively sure it is, given its other properties. SAGE will tell a clearer picture.
Ninth thread starts with brief summary of the progress, including the following: we can now 6-color![[0,2]\times\mathbb{R}](https://s0.wp.com/latex.php?latex=%5B0%2C2%5D%5Ctimes%5Cmathbb%7BR%7D&bg=ffffff&fg=303030&s=0&c=20201002) .
.
It is strange, because we can do much more already using Pritikin’s style design, as it was described here:
One should use the same infinite design without round boundaries. It gives the width
The starting points for 4- and 5-coloring are![[0,1]\times\mathbb{R}](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5Ctimes%5Cmathbb%7BR%7D&bg=ffffff&fg=303030&s=0&c=20201002) (triangles) and
(triangles) and ![[0, \frac{13}{8}]\times\mathbb{R}](https://s0.wp.com/latex.php?latex=%5B0%2C+%5Cfrac%7B13%7D%7B8%7D%5D%5Ctimes%5Cmathbb%7BR%7D&bg=ffffff&fg=303030&s=0&c=20201002) (pentagons) respectively.
(pentagons) respectively.
No,![[0,\frac{\sqrt3}{2}]\times\mathbb{R}](https://s0.wp.com/latex.php?latex=%5B0%2C%5Cfrac%7B%5Csqrt3%7D%7B2%7D%5D%5Ctimes%5Cmathbb%7BR%7D&bg=ffffff&fg=303030&s=0&c=20201002) for 4-coloring.
for 4-coloring.
String of truncated circles gives![[0,\frac{\sqrt3}{2}]\times\mathbb{R}](https://s0.wp.com/latex.php?latex=%5B0%2C%5Cfrac%7B%5Csqrt3%7D%7B2%7D%5D%5Ctimes%5Cmathbb%7BR%7D&bg=ffffff&fg=303030&s=0&c=20201002) for 3-coloring and
for 3-coloring and ![[0,\frac{\sqrt8}{3}]\times\mathbb{R}](https://s0.wp.com/latex.php?latex=%5B0%2C%5Cfrac%7B%5Csqrt8%7D%7B3%7D%5D%5Ctimes%5Cmathbb%7BR%7D&bg=ffffff&fg=303030&s=0&c=20201002) for 4-coloring.
for 4-coloring.
And pentagons can give better result for 5-coloring: . It is just a half of Pritikin’s style design for 6-coloring.
. It is just a half of Pritikin’s style design for 6-coloring.
No, this is wrong again. One should return to .
.