Given the initial activity on the Polymath proposal page, Terry Tao suggested that Aubrey de Grey and I launch Polymath16 to make progress on the Hadwiger–Nelson problem. This project is a follow-up to Aubrey’s breakthrough result that the chromatic number of the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki page.
The Hadwiger–Nelson problem is that of determining the chromatic number of the plane (CNP), defined as the minimum number of colours that must be assigned to the points of the plane in order to prevent any two points unit distance apart from being the same colour. It was first posed in 1950 and was reduced the following year to a finite graph problem; in particular, CNP is at least k if and only if there exists a finite graph of chromatic number k that can be drawn in the plane with each edge being a straight line of unit length. Such graphs are termed unit-distance graphs. It is easy to find 4-chromatic unit-distance graphs, the smallest being the 7-vertex Moser spindle.
In April 2018, Aubrey posted to the arXiv a report [deG2018] of a family of 5-chromatic unit-distance graphs. However, the smallest such graph that he discussed has 1581 vertices, and its lack of a 4-colouring requires checking for the nonexistence of particular types of 4-colourings of subgraphs of it that have almost 400 vertices, which requires a computer search.
This has led to interest in the search for simpler examples. Along these lines, our goals for this project are quite varied:
Goal 1: Find progressively smaller 5-chromatic unit-distance graphs. The current record is 1577, and recent insights promise to lead to further progress soon.
Goal 2: Reduce (ideally to zero) the reliance on computer assistance for the proof. Computer assistance was leveraged in [deG2018] to analyze a subgraph of size 397. This has so far been decreased to 278, though the corresponding full graph is actually larger than Aubrey’s original one.
Goal 3: Apply these simpler graphs to inform progress in related areas. For example:
- Find a 6-chromatic unit-distance graph.
- Improve the corresponding bound in higher dimensions.
- Improve the current record of 105/29 for the fractional chromatic number of the plane.
- Find the smallest unit-distance graph of a given minimum degree (excluding, in some natural way, boring cases like Cartesian products of a graph with a hypercube).
Following guidance from Terry Tao, we are setting a deadline for this project at Apr 15, 2019.
See this page for a newcomer’s guide to the initial approach of this project. In the short term, we are working to make further progress on Goals 1 and 2 by stitching together newly identified graphs that can substitute for the building-blocks L and M in [deG2018] and then passing them through shrinking routines of the sort described in section 5 of [deG2018].
To properly document progress on these goals, it might be helpful for participants to post links to files that contain coordinates of points in the plane and/or the resulting unit-distance graph. I launched a Dropbox folder that can serve as a repository of such files. Participants who wish to contribute a file to this folder should email me so I can grant editing privileges or post the file myself.
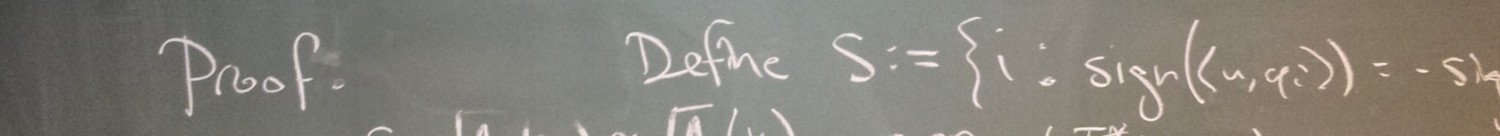
Many thanks Dustin! I am delighted to say that this introductory post became out-of-date just minutes before you posted it 🙂 I will ask Marijn to re-post his improvement here.
Some remarks about the Hadwiger-Nelson problem of coloring the unit-distance graph of the plane, III
In this post I’d like to consider a “reversed” approach to the problem, roughly pick your graph first, then embed it as a unit-distance graph second.
That way the chromatic number would be trivial to find (design graph to have the one you want). The hard part is the embedding – if even possible. This way of thinking also leads to other useful conclusions and/or speculations, the coolest being the speculation that de Grey’s configuration is best possible, i.e. cannot be pushed to chromatic number 6.
Also, why are we focusing on the Euclidean plane?? Suppose we instead ask: what is the chromatic number of the surface of a sphere? Or of the hyperbolic nonEuclidean plane? These more-general questions seem more interesting. The answers to these questions would depend on the specific distance chosen. I.e. for the Euclidean plane, where two points are “joined by an edge” if distance=S, the chromatic number does not care about the value of S>0. For a unit-radius sphere, though, it might care, and would depend upon S with 0<S<pi (if we are measuring S geodesically). In that case it is of especial interest to enquire about the MAXIMUM over all S with 0<S=3 and ChromNumber(hyperbolic plane)>=3 regardless of the value of S. Indeed for D-dimensional nonEuclidean space, ChromNumber>=D+1 shown by a regular simplex.
The “Moser Spindle” in fact also works in any nonEuclidean plane to show ChromNumber>=4 for almost any S, and indeed in any D-dimensional nonEuclidean space to show ChromNumber>=D+2. [To define the latter, glue two regular simplices on a common face, make two of the resulting objects share an apex, then adjust the angle at that common apex until the two far-apices have distance S from each other.]
Now suppose we have a V-vertex graph, and want to EMBED it on surface of unit sphere with all graph-edges same length. Let the xyz coordinates of the V vertices be the rows of a Vx3 matrix M. Each row has unit norm (since on sphere). M Mtranspose is a symmetric VxV matrix, and each entry ij of this matrix equals cos(S) whenever ij is a graph-edge. So the question of whether a V-vertex graph G can be embedded on (D-1)-dimensional surface of unit radius D-dimensional sphere (0<D=C, we need a graph (with minimal vertex count) to have all valencies>=C-1. (Because: Otherwise we could remove a min-valence vertex, color the rest with C-2 colors, then C-1 colors would suffice.) That means the number of edges has to be >=(C-1)*V/2 if there are V vertices. Each graph-edge, if of fixed length, constitutes one equation constraining embeddings. The number of degrees of freedom available to embed a V-point set on (D-1)-dimensional surface of D-dimensional sphere, is
V*(D-1) – (D-1)*D/2 + optional1
where the “optional1” means we get to add 1 if we get to freely choose the distance-value S as an addtiona “degree of freedom”; but if S is fixed and not under our control then 0. The (D-1)*D/2 arises by modding out by the D-dimensional rotations. So if
V*(D-1) < (D-1)*D/2 + (C-1)*V/2 – optional1
then the available number of degrees of freedom is not adequate (if each constraint effectively reduces the DoF's by 1); i.e. it is going to require a miracle for a graph with ChromNumber=C to be thus-embedded.
This leads us to the conclusion that, in the absence of miracles,
ChromNumber <= 2*(D-1) + 1
is the best we can hope for from a large point set (V large but D held fixed) on the (D-1)-dimensional surface of a unit sphere. For the Euclidean plane, use 2 in place of D-1, to conclude from analogous argument that
ChromNumber <= 5
in absence of miracles.
This suggests that Aubrey de Grey's point set MAY BE OPTIMAL, i.e. the only way anybody will ever find a 6-chromatic finite point set in the plane, is either via "miracles" (or if the point set has unreasonably small cardinality) !!!
What I mean by "miracle" is, sometimes it can happen that a bunch of numbers satisfies some set of equations even though we did not try to make them do that. The more equations we get without asking, the more "miraculous" it is.
Hey, what the hell. Your worthless blog software obliterated some of the text I mouse-copied into it.
“In that case it is of especial interest to enquire about the MAXIMUM
over all S with 0<S" [AND HERE IT OBLITERATED A LOT] "=3 and…"
This should have read
"In that case it is of especial interest to enquire about the MAXIMUM
over all S with 0<S=3 and…”
Let me see if it actually says it now…
Let me see if it actually says it now…
–it did not!! It obliterated it AGAIN!! It appears there are forbidden
sentences that your blog software carefully edits out!!!
Totally worthless crap.
The problem is probably with angle brackets: HTML elements are surrounded by them, so the blog software might be removing anything that looks like it’s enclosed by angle brackets and isn’t on a short list of permitted terms).
Try using < and > for less-than and greater-than (note the semicolons). Inside LaTeX you can also use \lt and \gt .
I’m sorry – it seems \lt and \gt are not standard macros. So try < for < and > for > .
A known consequence of the “compactness thoerem” in formal logic is that An infinite graph G is n-colorable if and only if every finite subgraph of G is n-colorable. See
https://en.wikipedia.org/wiki/De_Bruijn%E2%80%93Erd%C5%91s_theorem_(graph_theory)
So, to the extent we take my argument seriously that it would be a “miracle” if any finite planar point set had ChromNumber>5, we in fact would have to go further — it indicates that the SOLUTION OF THE HADWIGER-NELSON PRIOBLEM MUST BE 5, barring miracles.
But it is not clear to me that miracle-exclusion really means a lot in this case. Almost always in my prior mathematical experience, this sort of “counting equations vs counting unknowns” argument has yielded the right answers about existence/not of solutions, because miracles really usually cannot happen.
BUT for our particular problem here, we know that some highly-related miracles CAN happen in a big way. Namely, in the Eisenstein integers (triangle lattice points in plane) the graph arising from SquaredDistance=K, where K is any integer with a large number of distinct Eisenstein prime factors, is a regular graph with arbitrarily large valency. Which means this is an arbitrarily large miracle (valencies bounded below by anything above 4 being “miraculous”).
Here are some values of K yielding “miraculously large” valencies:
K: 1, 7, 49=7*7, 91=7*13, 637=7*7*13, 1729=7*13*19, 8281=7*7*13*13,
yielding valencies
6, 12, 18, 24, 36, 48, 54.
But still, the argument has value in the sense that it tells you, if you want to go for ChromNumber 6, you need to intentionally construct and take advantage of such “miracles.”
In general, your suggestion to start with the graph and find a unit-distance embedding seems to be feasible in practice if the number of vertices is small. I have done exactly that when finding the embeddings described here:
https://mathoverflow.net/q/244604/39495
(From a coloring perspective, the Hadwiger graph is not interesting, since it is bipartite, but the embedding given on the top right in the mathoverflow post gives an extra edge between vertex 1 and 12, already making the graph not 2-colorable any more)
Perhaps it would be a good idea to compile a list of small graph, which are not 4-colorable and good candidates for being unit-distance graphs (which are relatively sparse and don’t contain any obvious non-unit-distance subgraphs..)
Here is another QUESTION.
Suppose a point set P in the plane contains NO unit distances. What is the maximum possible fraction of the measure of a large ball (in the limit of infinite radius) contained in P?
For the 1D version of this problem, the answer is 1/2. Therefore by “sterology” it follows that 1/2 is an upper bound on the answer to our 2D problem. Better upper bound is 1/3 by arguing for any eq.triangle with unit sides at most one of its 3 vertices lies in P. Better upper bound is 2/7 by arguing for any Moser spindle at most 2 of its 7 vertices lie in P. Maybe an even better bound arises from some of the graphs found by de Grey and successors; but need to find maximum independent set in those graphs to get bounds.
A lower bound is 1/7. But a better lower bound is 1/4 by taking the integer square grid with unit sidelength, and filling the grid-squares whose lower left corner has (even,even) integer coordinates, with black paint.
Correction
“But a better lower bound is 1/4 by taking the integer square grid with unit sidelength, and filling the grid-squares whose lower left corner has (even,even) integer coordinates, with black paint.”
–That was wrong because some unit distances fit inside each black square (go diagonally).
Correct this by only painting the incircle of that square black, then revised (not as good) lower bound is: pi/16.
We can improve that by considering the hexagonal “beehive” tesselation of the plane, 4-coloring the hexes, and then in each red hex, you put an incircle and paint it black. (Diameter of circle is 1.) Then the lower bound you get is
(1/4) * (area of incircle / area of regular hexagon)
= pi/(8*sqrt(3)) = 0.22672492…
A slight refinement of your hexagonal “beehive” tessellation gives the best known lower bound since 1967. See the discussion on page 2 here:
https://arxiv.org/abs/1501.00168
Also, you might find this survey interesting:
http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=8F6A67AFCBDAB161827B5D53FFA1009B?doi=10.1.1.642.8688&rep=rep1&type=pdf
Er, yes. I was about to correct my hex beehive thing, before you pointed this out.
The correction is as follows. Take the “penny packing” of equal unit-radius discs at max density in the plane. Now shrink each penny a factor 2 in radius (same disc center) so now have diameter=1. The resulting set of points in the plane is free
of unit distances and has density pi/(8*sqrt(3))=0.22672492…
as opposed to the upper bound from random Moser spindles which is 2/7=0.285714…
The paper you cite improves the lower bound to 0.22936
and the upper bound to 0.258795.
I was able to compute a unit-distance graph with chromatic number 5 with 874 vertices and 4461 edges. The graph is available here:
* http://www.cs.utexas.edu/~marijn/CNP/874.vtx
* http://www.cs.utexas.edu/~marijn/CNP/874.edge
The first file lists the vertices in the format of Mathematica, while the second file shows the graph as list of edges in the DIMACS format.
I observed that the following graph has chromatic number 5: Start with two copies of graph M (or the reduced M based on Tamás Hubai’s suggestion to trim W with a radius of sqrt(6+sqrt(33))/3 instead of sqrt(3)) and let’s call them M1 and M2. Rotate M2 using point {1,0} as center such that the distance between point {-1,0} in M1 and the corresponding point in M2 is 1. The 874-vertex graph is a subgraph of M1 + M2. I used SAT solving techniques based on proofs of unsatisfiability for the reduction. As mentioned in an earlier post, this progress can be randomized. Smaller graphs can probably be obtained by performing multiple such random probes.
Nice! Does M1 + M2 denote the Minkowski sum of M1 and M2?
With M1 + M2 I denote the union of points in M1 and M2 with an edge between a pair of points if and only if their distance is exactly 1.
Thomas Sauvaget emailed me some visualizations of this graph. The second vertex has the largest degree (50), and its edges are colored in red below:
Do you know what he used to make these graphs?
To answer David Lowrty-Duda’s question, I’ve done it in R, but note that Marijn Heule’s visualization of his 826-vertices graph below is much better.
If you still want to use R, after processing the initial vertices data, in particular using the following function to turn the algebraic expressions into nums :
m=apply(X=verticespositions, MARGIN=2, FUN=function(this.col) sapply(X=this.col, FUN=function(x) eval(parse(text = x))))
and taking the edges data, simply construct a big dataframe that has 4 variables : coordinates of the beginning and end of each edge, then use the ‘segments’ function (first make sure you set up the plotting range correctly).
I computed the Lovasz theta function value at the complement of your graph and it is in the interval [3.3746, 3.3748].
Some remarks about the Hadwiger-Nelson problem of coloring the unit-distance graph of the plane
1. It is best to regard it as the complex plane z=x+i*y, not the (x,y) plane.
2. Then dist(a,b)=|a-b|, and rotating and scaling and translating a point s is a*s+b, where the translation is b, the scaling is |a|, and the rotation angle is arg(a). Reflecting s about the real axis is accomplished by ComplexConjugate(s), written as s with an overbar.
3. Let W=[-1+sqrt(-3)]/2=exp(2*pi*i/3) so that
W^3=1 and (W+1)^6=1 and sqrt(W)=W+1.
The “Eisenstein integers” E consist of the integer linear combinations of W and 1, that is E=a+b*W where a and b are integers. Arithmetically, they form a ring. We have |E|^2=a^2-a*b+b^2 so the interpoint distances are exactly the square roots of integers representable in the form a^2-a*b+b^2.
4. When Q and D are positive integers, define the “Eisenstein graph” EG(Q,D) to be: The vertices are the Eisenstein integers E with |E|^2<=Q. The edges are the interpoint distances equal to sqrt(D). A good computer project for anybody with access to a good graph-coloring program, would be to compute the chromatic numbers of EG(Q,D) for all small 2-tuples (Q,D) of natural numbers. This perhaps could provide a very simply defined single-distance-graph in the plane, whose chromatic number was 5, 6, or 7. Even if not, it still would be nice to have some idea how the chromatic numbers of the EG's behave.
5. The "Moser spindle" M is a 7-vertex 11-edge unit-distance graph with chromatic number 4. All valencies are 3 except for one 4. We may just regard M as this 7-point set in the complex plane:
M = {0, 1, 1+W, 2+W, A, A+A*W, 2*A+A*W}
where 0 is the 4-valent vertex, W=[-1+sqrt(-3)]/2=exp(2*pi*i/3) as before, and
A=exp(i*2*arcsin(1/sqrt(12)))
=exp(i*2*arccot(sqrt(11)))
=exp(i*arctan(sqrt(11)/5))
=exp(i*arccos(5/6))
=exp(i*arcsin(sqrt(11)/6))
=[5+sqrt(-11)]/6
=0.8333333… + 0.55277079839256664151915545611178111398784809093155893284… i
Incidentally the square root of A is
sqrt(A)
=[sqrt(33)+sqrt(-3)]/6
=0.95742710775633810997510191136982155303671074299713206128… +
0.28867513459481288225457439025097872782380087563506343800… i
A fairly obvious computerized approach to seeking chromatic number 5 then is to take the union of many translated-and-rotated copies of M, trying to choose the translations and rotations in such a way as to get a lot of unit distances and to minimize the number of vertices with small valencies. Hopefully one can thus obtain some set R of points, whose unit-distance graph has chromatic number 5. If you succeed, then you can remove unneeded points to get a simpler R. As far as I can tell, this is precisely what Aubrey de Grey and Marijn Heule did, albeit de Grey was cleverly keeping some graph properties in mind as he went.
6. The Eisenstein integers are generated additively from 1 and W, regarding them as an additive group. And since W^3=1 we can in fact generate them from W alone, now generating both additively and multiplicatively and regarding them as a ring.
A now-natural algebraic structure to consider is what I will call the "Moser ring" which we can generate additively and multiplicatively from W and A.
Although the Eisensteins form a triangular lattice in the plane with nearest-neighbor separation 1, the Moser ring is everywhere dense in the plane, due to the irrationality of arccos(5/6) in degrees (33.5573097619207… degrees). If, however, we (roughly speaking) refuse to multiply more than a constant number of times, then we can obtain subsets of this ring having bounded density…
7. One of Marijn Heule's point sets has 874 points and 3642 unit distances, and chromatic number 5. It lies within the ring generated additively and multiplicatively from
{1, i, Sqrt[3], Sqrt[5], Sqrt[11]}/96.
It would be nice to try to reduce the number of multiplicative and/or additive generators needed to produce this ring. I claim the following 3 generators suffice, by multiplication and addition, to generate (Heule's point set scaled up by a factor of 24):
{W, sqrtA, sqrtB}
where
B = [7+sqrt(-15)]/8
and
sqrt(B)=[1+3*sqrt(5)+sqrt(-3)+sqrt(-15)]/8.
This ring of course contains the Moser ring as a subring, and the Eisensteins as a subsubring.
8. Once a reasonably small set R were found, it then would be natural to seek a 6-chromatic set, by taking the union of many translated-and-rotated copies of R, trying to choose the translations and rotations in such a way as to get many unit distances and to minimize the number of vertices with small valencies.
9. And if one (call it H for "holy grail") were found, it then would be natural to seek a 7-chromatic set, by taking the union of many translated-and-rotated copies of H, trying to choose the translations and rotations in such a way as to get many unit distances and to minimize the number of vertices with small valencies.
corrections to my previous post:
1. The ring contains “Heule’s point set scaled up by a factor of 24”
— should have said 48 not 24.
2. “One of Marijn Heule’s point sets has 874 points and 3642 unit distances”
–should have said 4461 unit distances.
The important thing is that everything is contained in the ring generated additively
and multiplicatively by the 3 complex numbers I called W, sqrtA, and sqrtB.
Furthermore, Heule’s 874-point set (scaled up by 48) not only is contained inside the ring generated by {W,sqrtA,sqrtB}, it is contained inside the additive group generated by these 30 complex numbers:
(powers<=2 of W) * (powers<=3 of sqrtA) * (powers<=5 of sqrtB)
i.e. the subset of the ring got by refusing to use too many multiplications.
Oh, and it should be noted that W, sqrtA, and sqrtB all are UNIT-NORM complex numbers.
So: Heule’s 874-point configuration could have been discovered by “brute force” by:
1. start with those three particular complex numbers {W,sqrtA,sqrtB},
2. perform a limited number of multiplications, additions, and subtractions to generate a larger but finite point-set (each point is a complex number) [one must specify the bounds on how many operations of each type are permitted, but one could just keep increasing the bounds until succeed)
3. run resulting graphs (that arise from only using a particular distance as an “edge” – try all eligible distances starting with the most popular as “the” distance) thru a coloring algorithm.
The particular distance that worked is 48. Others might also work. The max number of multiplications needed was 2+3+5=10. The max number of +/- needed is… I’m not sure, but not very large, probably 15 or so suffices?
Regarding 4, David Speyer shows here that they are all (at most) 3-chromatic: https://polymathprojects.org/2018/04/10/polymath-proposal-finding-simpler-unit-distance-graphs-of-chromatic-number-5/#comment-120359
He also suggests another ring to look at.
Yes, I had in the meantime also noticed Speyer. I may have more to say about that and “good” choices of rings, later. For now, I remark that in view of the fact that
x^5 = square(square(x))*x is computable with only three multiplications,
and x^3 with only two, and x^2 with only one,
the max number of multiplications needed starting from my three generators W, sqrtA, sqrtB, is 3+2+1+1+1=8, improving over 10 which I’d said before.
I have not made any careful attempt to bound the number of additions & subtractions needed.
Some remarks about the Hadwiger-Nelson problem of coloring the unit-distance graph of the plane, II
In this post I will make speculations about the nature of “good” rings of complex algebraic numbers, “good” meaning hopefully containing point-sets whose unit-distance graphs have high chromatic number.
But first to reiterate and correct my earlier post. There I had noted (I have a computer program which tediously verified this claim… except for bugs in my brain…) that Marijn Heule’s 874-point 5-chromatic set lay within the ring generated additively and multiplicatively from these 3 complex numbers:
G1, G2, G3
and at most 8 multiplications were needed, everything else being additions or subtractions.
I had there denoted these
G1=W, G2=sqrt(A), G3=sqrt(B).
But unfortunately the number I had called B was not actually the square of the generator G3 which I had called sqrt(B), it actually was
G3^2 * W.
Sorry about that. This error does not matter in the sense that my program still verified that G1,G2,G3 did generate. It also did not matter in the other sense that
sqrt( G3^2 * W ) = G3 * sqrt(W)
and sqrt(W) = W+1 already was in the Eisenstein ring, so that ALSO would have been a legitimate generator we could have replaced G3 with, if we prefer it.
I now give numerous expressions for these particular three magic numbers:
G1 = W
= [-1+sqrt(-3)]/2
= exp(2*pi*i/3)
= -0.50000+0.86602540378444*i
= exp(i*120.000000 degrees)
so that
W^3=1 and (W+1)^6=1 and sqrt(W)=W+1.
G1 by itself generates the “Eisenstein integers” which contains the equilateral triangle, simplest 3-chromatic set.
G2 = sqrt(A)
=[sqrt(33)+sqrt(-3)]/6
=exp(i*arccot(sqrt(11)))
=exp(i*arccos(sqrt(11/12)))
=exp(i*arcsin(1/sqrt(12)))
=0.95742710775633810997510191136982155303671074299713206128… +
0.28867513459481288225457439025097872782380087563506343800… *i
=exp(i*16.778655 degrees)
G2^2 = A
=[5+sqrt(-11)]/6
=exp(i*2*arcsin(1/sqrt(12)))
=exp(i*2*arccot(sqrt(11)))
=exp(i*arctan(sqrt(11)/5))
=exp(i*arccos(5/6))
=exp(i*arcsin(sqrt(11)/6))
=0.8333333… + 0.55277079839256664151915545611178111398784809093155893284… i
=exp(i*33.557310 degrees)
{G1, G2^2} generate the “Moser ring,” which includes the “Moser spindle” simplest 4-chromatic set.
G3=[1+3*sqrt(5)+sqrt(-3)-sqrt(-15)]/8
=exp( i*(arcsin(1/4) – pi/6) )
=exp( i*arctan(sqrt(3)*(sqrt(5)-4)/11) )
=exp( i*arcsin( (sqrt(3)-sqrt(15))/8 ) )
=exp( -i*arccos( (1+3*sqrt(5))/8 ) )
= 0.96352549156242113615344012577422858829023188485432214660… –
0.26761656732981744895647738228456590548626455643515127481… *i
= exp( -i*15.522488 degrees)
{G1, G2, G3} generate a ring that includes Marijn Heule’s 874-point 5-chromatic set.
G3^2 * G1 = [7+sqrt(-15)]/8
=exp(i*arctan(sqrt(15)/7))
=exp(i*arccos(7/8))
=exp(i*arcsin(sqrt(15)/8))
=exp(2*i*arccot(sqrt(15)))
=exp(2*i*arccos(sqrt(15)/4))
=exp(2*i*arcsin(1/4))
=0.875 +
0.48412291827592711064740817497279995135411521316144885332… *i
=exp(i*28.955024 degrees).
Now meanwhile I noticed (plus Boris Alexeev told me) that David Speyer had shown that EVERY single-distance graph inside the Eisenstein integers, is at most 3-chromatic.
Speyer also showed every single-distance graph inside the Gaussian integers (integer linear combination of {1,i}), is at most 2-chromatic.
I now re-explain Speyer’s arguments.
In the Gaussian integers, the UFT (unique factorization theorem) states that
1. every Gaussian is a product of “Gaussian primes.” This product is unique up to reordering and multiplications by the “units” +-1, +-i.
2. the Gaussian primes are: a+b*i where a^2+b^2 is an ordinary prime, and p where p is an ordinary prime not expressible as a sum of two squares, equivalently p that are congruent to 3 mod 4.
Examples:
1+i, 1-i, and 1+2*i are Gaussian primes since 2 and 5 are primes.
3 and 11 are Gaussian primes since not a sum of two squares.
Primality is unaffected by multiplication by a unit.
Speyer’s argument is that the single-distance (squared so it is an ordinary integer) is wlog ODD, since if all squared distances were even we could scale the following argument up by a factor of 1+i. And then every edge moves us from a point a+b*i to another c+d*i where a+b and c+d necessarily have DIFFERING PARITIES, hence graph is bipartite, Q.E.D.
Equivalently, each edge moves us to a different residue class modulo 1+i. There exactly are 2 such residue classes.
In the Eisenstein integers, the UFT says
1. every Eisenstein is a product of “Eisenstein primes.” This product is unique up to reordering and multiplications by the six “units” (6th roots of unity).
2. the Eisenstein primes are: a+b*W where a^2-a*b+b^2=|a+b*W|^2 is an ordinary prime not congruent to 2 (mod 3), and p where p is an ordinary prime with p=2(mod 3). Primality is unaffected by multiplication by a unit.
Speyer’s argument is that the single-distance (squared so it is an ordinary integer) is wlog INDIVISIBLE BY 3, since otherwise we could scale the following argument up by a factor of W-1. And then every edge moves us from a point a+b*W to another c+d*W in a DIFFERENT coset of (the Eisensteins times W-1). Hence graph is tripartite, Q.E.D.
Equivalently, each edge moves us to a different residue class modulo W-1. There exactly are 3 such residue classes.
More generally, I claim that in any ring of algebraic complex numbers which enjoys UNIQUE FACTORIZATION into “primes,” and whose elements all have integer-valued norms (norm means length-squared of complex number), the Speyer-like argument should tell us that any single-distance graph must have chromatic number C or less, where C is the least integer-valued “norm” of any PRIME in that ring.
For rings which do NOT enjoy unique factorization (which is to say – most of them!) and especially if they are DENSE regarded as complex point-sets, Speyer-like arguments are going to tell us little or nothing. And what I have been calling the “Moser ring” is a dense set. I personally doubt that any non-dense ring is going to be useful for the Hadwiger-Nelson problem in which case Speyerness would be useless. If, however, one IS useful, then that would be very cool, and Speyerness probably will be very useful in removing lots of bad options frm consideration.
So the question now is: which rings are “good”?
Observe that the law of cosines from trigonometry states that
H^2 = a^2 + b^2 – 2*a*b * cos(T)
for a triangle with legs a,b, hypotenuse H, and apex angle T. It is natural to add to our present ring, a new element selected to cause there to be a new unit-distance |H|=1 available. That suggests adding to the picture, the complex number
exp( i*arccos( (1-|a|^2-|b|^2)/(2*|a|*|b|) ) )
where a and b are elements of the old ring. We then get a new extended ring. The “greedy” choice is to choose a and b to be elemnts of least-possible norms |a| and |b| such that somethign nontrivial happens.
Let us try that greedy ring-building process out.
1. Begin with the ordinary integers Z. (Chromatic number=2 from 1-edge graph.)
2. Element of least norm (above 0): 1.
3. Adjoin
exp( i*arccos( (1-1^2-1^2)/(2*1*1) ) )
=exp( i*arccos( -1/2 ) )
=exp( i*2*pi/3 )
4. Well, golly gee, we now have the Eisenstein integers. They yield chromatic number=3.
5. Element of least norm (above 1): |W-1|=sqrt(3).
6. Adjoin
exp( i*arccos( (1-3-3)/(2*3) ) )
= exp( i*arccos( -5/6 ) )
= -exp(i*33.557310 degrees)
= -G2^2
this is the negated Moser generator, and negation is irrelevant since -1 is already in the ring, so, golly gee, we now have the Moser ring. They yield chromatic number=4.
7. Well, now there is no least-norm Moser since it is a dense ring. But if we restrict attention to some natural nondense subsets, the small Eisenstein lengths are
1, sqrt(3), 2, sqrt(7), 3, sqrt(12), sqrt(13), …
(see http://oeis.org/A004016) so if we choose the least available we have not already used, namely 2, that would suggest adjoining
exp( i*arccos( (1-4-4)/(2*4) ) )
= exp( i*arccos( -7/8 ) )
= -exp(i*arccos(7/8))
= G3^2 * G1
and since G1 and -1 already are in the ring (the Eisenstein generator), golly gee, we now have a subring of the 5-chromatic (Heule 874) ring which is a superring of the Moser ring. The reason it is a subring is we were, essentially, adjoining G3^2 and not G3.
So… now I am a bit confused: why the angle-halving, aka square-rooting, to get G2 from G2^2 and G3 from G3^2?
8. Anyhow this suggests that good candidates for adjoining to the present ring, to get a new bigger ring that perhaps can get us up to chromatic number 6, might be:
exp( i*arccos( (1-7-7)/(2*7) ) ) = exp( i*arccos( -13/14 ) )
or
exp( i*arccos( (1-9-9)/(2*9) ) ) = exp( i*arccos( -17/18 ) )
or their square-roots. Other natural candidates can also be dreamed up by similarly employing the law of cosines to small leg-lengths arising from simple elements of the ring we already had, to deduce angle, then exp(i*angle) is the natural nnew generator to consider, or if we believe in the mysterious Magical Square Rooting then exp(i*angle/2).
I’ve been thinking more about the quadratic rings situation, so let me address it here. Summary: The first situation where we could have a hope of finding a graph needing 6 colors is![\mathbb{Z}[\tfrac{1+\sqrt{-71}}{2}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Ctfrac%7B1%2B%5Csqrt%7B-71%7D%7D%7B2%7D%5D&bg=ffffff&fg=303030&s=0&c=20201002) , looking at vectors of length 60, in other words, solutions to a^2+71 b^2 = 14400. The (a,b) values in question are ((120, 0), (93, 9), (49, 13), (22, 14)), and the variants of these where we insert minus signs.
, looking at vectors of length 60, in other words, solutions to a^2+71 b^2 = 14400. The (a,b) values in question are ((120, 0), (93, 9), (49, 13), (22, 14)), and the variants of these where we insert minus signs.
Let L be the lattice of pairs of integers (a,b) with a = b mod 2. Embed this in the plane by (a,b) —> (a, b sqrt(71))/120. Then the above list shows that the unit distance graph on L is 18-regular. It is easy to check that this graph is connected. The inclusion of (120,0) = 60 * (2,0) ensures that coloring modulo any index 2,3,4,5 or 6 lattice will not work.
A back of the envelope computation suggests that a random d-regular graph is likely to be c-colorable as long as . (Does anyone know better analysis?) That suggests that an 18 regular graph is probably not 5-colorable but is probably 6-colorable, and we need to go up to 20-regular to force 7-colors.
. (Does anyone know better analysis?) That suggests that an 18 regular graph is probably not 5-colorable but is probably 6-colorable, and we need to go up to 20-regular to force 7-colors.
I’ll upload the number theoretic details of why 71 and 14400 are the first case to try when I get a chance this weekend.
(This is a reply to David’s nested comment.)
Thanks for your suggestion; I might try it out. As far as I can tell, however, the graph you mention is 14-regular and thus heuristically 5-colorable by your argument. It would be 18-regular if there were one more solution to your squared norm equation with a and b positive. Am I mistaken?
I’ve started to add some of the new graphs used in this discussion to the table in the wiki at http://michaelnielsen.org/polymath1/index.php?title=Hadwiger-Nelson_problem . A reasonable naming system I think would be to denote the graphs by the letter of the analogous graph in Aubrey’s paper, subscripted by the next available natural number, e.g. the new G-type graphs can be named as they are discovered. Hopefully this will make it easy to refer to various graphs unambiguously. For some graphs I don’t have a good link to a place where one can find the graph described, so some further fleshing out of the table will be needed.
as they are discovered. Hopefully this will make it easy to refer to various graphs unambiguously. For some graphs I don’t have a good link to a place where one can find the graph described, so some further fleshing out of the table will be needed.
Also I added a section for further questions to explore, which I initially populated from some previous comments in older blog posts.
Many thanks Terry. We sure need some better nomenclature here. I am still on the road but I hope to come up with a good scheme over the next couple of days.
At the moment, we have an L whose properties can be verified by hand, but an M whose properties require a computer to check. In pursuit of Goal 2, it might be useful to weaken M so that it merely prevents vertices of a particular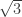 -regular triangle from being monochromatic. This would require a stronger L, but it might make both graphs amenable to by-hand analysis. I wonder how small Marijn Heule can make such a weakened version of M by removing vertices from his current M. In the meantime, I will think about constructing this by hand.
-regular triangle from being monochromatic. This would require a stronger L, but it might make both graphs amenable to by-hand analysis. I wonder how small Marijn Heule can make such a weakened version of M by removing vertices from his current M. In the meantime, I will think about constructing this by hand.
Totally agreed Dustin. In effect, by comparison to my construction we have simplified L down to just three points (a triangle of edges 2,2,1) and H to two points 2 apart, but our simplifications of M have been purely empirical and have provided no insight into what makes M so special in the first place. We now know that M as originally defined is even more special than it seemed, because the “spindling” of two copies of it that Marijn found would not work if all that was special about M was that its central H could not have a mono triangle – and indeed, confirming this, Marijn’s earlier experiments looking for only that property got it down to 270 or so, whereas for the new M1+M2 thing it is around 874/2.
Note, however, that (as Marijn said) an M that merely prevents vertices of a particular \sqrt{3}-regular triangle from being mono would not actually require any strengthening of L, because we could just slot two M’s into each H in L, with relative rotation 60%.
However, this doesn’t mean that the issue of how to find a stronger L should be ignored. For example, can we find one in which at least one copy of H must have two mono triangles? I sure can’t see one, but it might be possible, and then M could be weaker still, since it would only need to enforce that one of the two triangles of a given (presumably central) H was mono.
60 degrees, I meant of course 🙂
Would this really help? I mean there are only 4 ways to color H – let’s call them H2tri, H1tri, Haxissym, Hcentralsym in the order they appear in your paper. Graph L shows that we can suppose that at least one H is colored as H2tri or H1tri. Then graph M shows that this leads to a contradiction.
Denote a graph that would lead to a contradiction from H2tri by M2tri, and one that would lead to a contradiction from H1tri by M1tri. Obviously, M2tri union M1tri can also serve as an M, so at least one of these graphs cannot be much smaller than the smallest M. (In fact, I would conjecture that one of them equals the smallest M.)
Btw, as I wrote earlier (on the first polymathproject thread), a construction similar to L shows that at least one H is colored H1tri or Haxissym. Maybe someone could check how the size of the smallest known Mxxx varies for different colorings of H. (Note that for Haxissym and Hcentralsym we haven’t yet found any M.)
While attempting to find a small M that precludes certain monochromatic triples, I found a small M (i.e., 11 vertices) that precludes certain monochromatic quadruples.
Notice that any pair of points of distance less than 2 have two common neighbors in the plane. Consider any partition of the Moser spindle’s vertices into 3 pairs and a remaining vertex v such that each pair has a common neighbor that is not a vertex of the Moser spindle. Fix such a common neighbor for each pair and then pick any point of unit distance from v to produce a 4-vertex set H. Then every proper 4-coloring of the plane prevents H from being monochromatic, since H being monochromatic would leave only 3 colors for the Moser spindle. As an explicit example, we can match vertices of the Moser spindle according to the spindle’s reflection symmetry, and then there are 2^4 choices for H that lie on the axis of symmetry.
So now M is extremely simple at the price of H being larger and less symmetric. Do these features then make it infeasible to find an L that forces a monochromatic copy of H?
I think this is a very nice idea, and in fact I don’t think that we need to “pick” an H, i.e., a monochromatic copy of any of the 16 (?) possible H would lead to a contradiction, so we can consider all of them excluded. This might lead to a fully human proof!
This general idea of attaching a 4-chromatic graph M to a frame L, thus prohibiting the vertices of the frame from being all the same colour, was actually the main thrust of the approach that (according to Soifer’s book) Paul O’Donnell took during his PhD. A promising way to make it work is to use M’s that are not rigid, and that is what led Paul to his main results on 4-chromatic graphs of arbitrary girth. My impression of why it failed is that the power we gain from non-rigidity is outweighed by the rise in the number of colourings.
Is it possible for someone to post the SAT code for colorability to the polymath16 wiki so that the new construction of Heule can be checked for vertices which can be removed without changing the chromatic number?
P.S. It seems that the previous thread answers this question: https://dustingmixon.wordpress.com/2018/04/10/the-chromatic-number-of-the-plane-is-at-least-5/#more-4876
(Glucose 4.0 was what was used with the best results for the first construction)
Apropos, I received a report today that the 20425 “daddy of them all” can be verified with Glucose in under five minutes on a standard laptop! I speculate that the ease of determining unsatisfiability must in some way arise from the high degree of modularity of the graph.
Let me migrate to this thread a comment from the proposal thread. ( https://polymathprojects.org/2018/04/10/polymath-proposal-finding-simpler-unit-distance-graphs-of-chromatic-number-5/#comment-120320 )
It is interesting (but perhaps known) to understand the situation for construvtions relevant for the Erdos unit distance problems. Famousely Erdos found a unit distance graph on n vertices with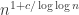 edges. The construction is (to the best of my memory) by looking at points
edges. The construction is (to the best of my memory) by looking at points 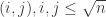 and choosing as edges the distance which occur most number of times. (I suppose the distance is some constant times \sqrt n.) Here are some questions:
and choosing as edges the distance which occur most number of times. (I suppose the distance is some constant times \sqrt n.) Here are some questions:
1) What is the chromatic number of this construction? (The upper bound 7 applies of course.)
2) Does this graph contains a Moser spindle? Maybe there is a related lattice-based graph with many Moser spindles? (Actually, does this graph contain triangles?)
Here are a few additional questions
3) Looking at Aubrey’s construction we may think that perhaps basing a similar construction on an Hexagonal lattice may have some advantages.
4) (rather wild) What can be said on the appearance of the most popular distance in an arrangement of points of the Penrose tiling?
5) Is there a “universal” unit distance graph (namely a unit distance graphs containing all small unit-distance graphs) ?
Let me also remind people of the Rosenfeld’s graph where two points are adjacent if their distance is an odd integers. The conjecture is tat this graph has infinite chromatic number. Again looking at the vertices in a square grid could shed some light on the problem.
Moshe Rosenfeld told me that the odd distance graph on contains no odd cycles hence is bipartite. (For Erdos’ example the required normalization need not be rational but it may be the case that this graph is also bipartite.)
contains no odd cycles hence is bipartite. (For Erdos’ example the required normalization need not be rational but it may be the case that this graph is also bipartite.)
It should be the two dimensional plane over the rationals.
Let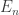 be the graph with vertices
be the graph with vertices 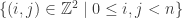 and edges when the distance is the most popular one.
and edges when the distance is the most popular one.
This is a subgraph of the graph with vertex set
with vertex set 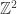 and edges given by the most popular squared distance
and edges given by the most popular squared distance 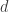 . Now note that mod 2,
. Now note that mod 2, 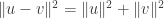 for all
for all 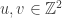 . If
. If 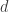 is odd this shows that
is odd this shows that  is bipartite, while if
is bipartite, while if 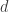 is even this makes
is even this makes  disconnected. Working mod 4 might show that each connected component is bipartite too.
disconnected. Working mod 4 might show that each connected component is bipartite too.
Experimentally, the most popular distance squared is odd (this the case for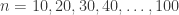 ).
).
I’ve posted to the Dropbox the grid graphs for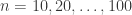 . Not sure if they’ll be useful since they are bipartite.
. Not sure if they’ll be useful since they are bipartite.
I find your “rather wild” idea of the Penrose tiling interesting because I have often wondered if quasicrystals could be used to lower the upper bound on the Hadwiger-Nelson problem to 6. The itself rather wild reasoning goes like this: The famous 7-coloring of the unit distance graph of the plane is constructed by partitioning the plane into the Voronoi cells of a lattice so that any cell is adjacent to 6 other cells, hence the chromatic number of the whole thing is 7. Perhaps there is some such quasicrystal S that every Voronoi cell of a member of S is adjacent to 5 other Voronoi cells of members of S. The reason for using quasicrystals is that they can have 5-fold rotational symmetry, so each point in S having 5 neighbours seems somehow appropriate. Is there any chance that this might work, or am I just blabbering?
In some sense, we can not hope to use tilings to improve the upper bound from 7, by a result of Carsten Thomassen.
On the Nelson unit distance coloring problem, Amer. Math. Monthly 106 (1999) 850-853.
Suppose each color class is a union of regions homeomorphic to topological disks, each region with diameter less than 1, and ever pair of regions separated by distance more than one. (So very general tiles!) Then he proves you need 7 colors!
I might be missing some technical condition, that the disks have to meet nicely along their boundaries, etc. But this is the jist of his result.
Thanks Lior Silberman and David Speyer (over the polymath blog) for the quick argument that distance-T graphs when the vertices are n by n integral grid are bipartite. A natural question that is related to comments by several commentators below (Warren D Smith, Craig, Varga) is to consider an extension of the integers by certain square roots (sqrt 3, sqrt 5,…) and still repeat the idea of taking distance-T graphs for a popular distance T. I wonder if we can add these graphs to the dropbox and perhaps check the numbers of edges and vertices, Moser Spindles, and perhaps chromatic number.
Gil: your suggestion can be interpreted in two different ways:
1. Replace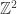 with a different quadratic ring (say
with a different quadratic ring (say ![\mathbb{Z}[\sqrt{3}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Csqrt%7B3%7D%5D&bg=ffffff&fg=303030&s=0&c=20201002) ), embedded discretely in
), embedded discretely in 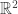 . This probably won’t be much different than the square lattice.
. This probably won’t be much different than the square lattice.
2. Replace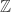 with the ring of integers of a number field (say
with the ring of integers of a number field (say ![\mathbb{Z}[\sqrt{3},\sqrt{5},\sqrt{11}] = \bigoplus_{d|3\cdot 5\cdot 11} \mathbb{Z}\sqrt{d}](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Csqrt%7B3%7D%2C%5Csqrt%7B5%7D%2C%5Csqrt%7B11%7D%5D+%3D+%5Cbigoplus_%7Bd%7C3%5Ccdot+5%5Ccdot+11%7D+%5Cmathbb%7BZ%7D%5Csqrt%7Bd%7D&bg=ffffff&fg=303030&s=0&c=20201002) ), that is take points each of whose coordinates is a point in the field. Now there are two problems: first, there may be multiple ways to embed the ring in the real numbers (this is not an issue for the repeated quadratic extensions used in the examples because they are Galois so the distinct embeddings all have the same image). Second, the image is dense in the real numbers. It is therefore not obvious how to make the graph finite.
), that is take points each of whose coordinates is a point in the field. Now there are two problems: first, there may be multiple ways to embed the ring in the real numbers (this is not an issue for the repeated quadratic extensions used in the examples because they are Galois so the distinct embeddings all have the same image). Second, the image is dense in the real numbers. It is therefore not obvious how to make the graph finite.
You can try to take a big box in the coordinates above, but the problem is that some directions are longer than the others. My guess is therefore to first embed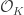 in
in  as a lattice and then take a big box (in other words, do lattice reduction to move from the basis
as a lattice and then take a big box (in other words, do lattice reduction to move from the basis  to a better one), and finally project on one of the coordinates.
to a better one), and finally project on one of the coordinates.
I’ll try implementing this later.
Dear Lior, what I had (perhaps naively) in mind is to consider, say, all points of the form (a+b sqrt 3, c+d\sqrt 3) where a,b,c,d are integers smaller than m. (and similarly when you add additional roots).
This is a feature request. Since people keep on replying to comments, new comments don’t always show up at the bottom, which makes it hard to track all threads. Could you maybe add a commentroll to the right (like the one on polymathprojects.org)? Preferably commentlinks should change color after clicking on them.
[Good idea! Done. – M.]
That was fast – thx a lot!
Actually, for me after clicking on it, the link remains blue – can you make it turn purple? This is less crucial, but for me it would help a bit.
I see that there is a cap of 3 on the reply depth (probably a good thing!). So this is a reply to Matthew’s post about Thomassen’s paper.
I am still a bit hazy about the definitions and so on, so I would be most grateful if anyone can correct me, but my understanding is that what Thomassen showed is that if there is a “tile-based” 6-colouring of the plane, meaning one in which for any point P there is a distance R such that all circles of radius at most R with centre P have each colour appearing only in at most one interval, then it must be unscaleable, i.e. the maximum diameter of a tile and the minimum separation of same-coloured tiles must both be exactly 1 (and the exclusion of distance 1 is achieved by suitable choice of colours of the points on the boundaries between tiles). Someone else showed earlier that there is no tile-based -colouring, but that’s all.
Gah, that last sentence was of course supposed to say “no tile-based 5-colouring”,
Using such a tessellation with polygons scaled to diameter one and choosing adequate boundaries I’ve found a 8-coloring with squares and triangles, both unscalable. Personally I think that using the exclusion zone defined by any polygon with more than 4 vertices yields a simplified graph with complete, or at least critical subgraphs with chromatic number 7 or higher, barring some miraculous tessellation no one has found yet.
These have been my personal observations independent from Thomassen but they seem directly related to what you’re describing. On the other hand I also haven’t come across a thorough definition of an exclusion zone that generalizes to any dimensionality and any input set (with a single color), so I’ve built one myself over the past 6 months.
I can add some information on this, but I will do so on the active thread.
[Again replying un-nested because of he cap on the nesting depth]
Domotor: You write “as I wrote earlier (on the first polymathproject thread), a construction similar to L shows that at least one H is colored H1tri or Haxissym”. I presume you are referring to your note of a construction in which “there’s always a right angle triangle with side lengths (1, sqrt(3), 2) whose 3 vertices have 3 different colors”. However, you didn’t tell us the construction 🙂 Please do!
Here is the argument (due to Tamas Hubai, September 2017):
If in a hexagonal lattice without H1tri and Haxissym, there is a H2tri, then every H in the hexagon lattice must be colored as H2tri.
If there is also no H2tri, then every H in the hexagon lattice is colored Hcentralsym.
In either case, vertices at distance 6 apart have the same color.
Therefore rotating the hexagonal lattice around one of its vertices (Moser-spindle-style) so that we get a triangle with side lengths (6,6,1), shows that in at least one of the two hexagonal lattices there is a H1tri or Haxissym.
Very nice!
I’m guessing that we should be able to combine the L’s we’ve been looking at (mine or Dustin’s) with Tamas’s – maybe by doing the rotation with respect to a longer distance, such as 12 – and thereby get an L in which at least one H must be H2tri That would then motivate further shrinking of our current M’s using the weaker constraint that the central H is not H2tri but can be either H1tri or the no-tri options.
I think combining the arguments would give an ‘L’ where at least one H must be H1tri (and not H2tri). As I’ve proposed yesterday, maybe someone could check how the size of the smallest known ‘M’ varies for the 4 different colorings of H. (Note that for Haxissym and Hcentralsym we haven’t yet found any M.)
H1tri, not H2tri, quite right.
It seems clear that at some point we are going to want to generalise the whole H,L,M construction strategy, so here’s an attempt to do so that might give us some ideas.
We represent our aspiring 5-chromatic graph A with with an abstraction that is a bipartite graph B. In this graph one of the independent sets of vertices, Hi, will correspond to graphs performing the role of H in our current construction, and the other vertices Li and Mi are the L’s and M’s. Then, to each edge {Hi,Lj} or {Hi,Mj} we assign a property Pij that is a subset of the 4-colourings of Hi. Finally, to each edge {Hi,Lj} (but not {Hi,Mj}) we assign a true/false flag Fij.
We can then exclude 4-colorability of A if there is no setting of the flags that satsfies two criteria: (1) for each Hi, the Pij of all of its edges whose other end is an M or whose flag is True have a non-null intersection; and (2) each Li has at least one edge whose flag is True.
The constructions we’ve examined so far are a very narrow subset of the above, represented by a star graph with a single L-type vertex at the centre, connected to a bunch of Hi that are each connected to one Mi. The Hi are all unit hexagonal wheel graphs, the Pi between them and L are the colourings of such a graph that have a mono triangle, and the Pi that connect to the Mi are the colourings that don’t have a mono triangle.
The idea here, of course, is that the intersections (within A) of vertices of the various graphs can be ignored: all the work of ensuring that A is not 4-colourable is done by the L’s and M’s imposing constraints on their component (i.e., neighbouring in B) H’s. The graph A is then shrinkable (initially just because there will be intersections of vertices), but the only graphs whose colourings need to be checked directly are the individual Mi and Li. Thus, in terms of Goal 2 we are looking simply to reduce the maximum size of those Li and Mi.
I think it’s probably too soon to make direct use of this abstraction, but it may become useful once we have accumulated a few more M’s and L’s with useful-looking properties.
Thoughts?
How far can we dream to push Goal 1? Marijn describes above a unit-distance graph 874 vertices and chromatic number 5. Pritikin shows here:
https://www.sciencedirect.com/science/article/pii/S0095895698918196
that every unit-distance graph on at most 12 vertices has chromatic number at most 4. Maybe it is worth thinking about how one might increase 12?
This would be a direction I would be quite interested in seeing pursued.
Is Pritikin’s good 5-coloring in the proof of Theorem 4 optimal?
As an alternative, fix a and b with a dividing b, and consider the good 5-colorings of that arise from coloring square tiles of side length a. Then we can iteratively apply a SAT solver to find the smallest n for which there exists such a coloring with n tiles colored 0.
that arise from coloring square tiles of side length a. Then we can iteratively apply a SAT solver to find the smallest n for which there exists such a coloring with n tiles colored 0.
I bet we’d get decent results with something like a=0.1 and b=4.
I’d be surprised if the construction in Pritikin can be beaten, but I really like your idea in principle – especially for the 6-colouring case that Pritikin essentially bailed on. I guess the question becomes whether the computation becomes infeasible before we get to useful values of b/a. But I hope someone here is tempted to try this
I now agree with Aubrey’s initial assessment of how hard this is. Indeed, an improvement to Pritikin’s good 5-coloring requires a color class (i.e., a set that avoids unit distances) with density larger than 0.22936. The color classes that Pritikin used came from Croft, and since their discovery in 1967, they’ve held the record as the densest known unit distance-avoiding sets. See this survey:
http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=8F6A67AFCBDAB161827B5D53FFA1009B?doi=10.1.1.642.8688&rep=rep1&type=pdf
Croft’s paper is difficult to access, but the following link provides a nice description of the construction:
https://arxiv.org/abs/1501.00168
I still haven’t given up hope on finding a good 6-coloring, although SAT solvers apparently interact poorly with constraints of the form “at most n vertices are colored 0.” Instead, we should restrict to a class of colorings over which minimizing the number of 0 vertices is a feasible enterprise. I’ve been discussing with Soledad Villar about the possibility of optimizing neural networks as coloring functions. More to follow.
Given it’s relation to Falconer’s famous work on the plane’s measurable chromatic number, I decided to ask MO if the literature contains any developments along these lines:
https://mathoverflow.net/questions/298198/how-much-of-the-plane-is-4-colorable
The random probing approach found a smaller unit-distance graph with chromatic number 5. This one has “only” 826 vertices and 4273 edges. The graph is available here (in the same formats as the prior graph):
* http://www.cs.utexas.edu/~marijn/CNP/826.vtx
* http://www.cs.utexas.edu/~marijn/CNP/826.edge
I generated a visualization based on a 5-coloring of this graph: http://www.cs.utexas.edu/~marijn/CNP/826.pdf
Great job Marijn!
I need to reorganise the wiki page to include a timeline for our progress. I hope to do that later this week.
Amazing progress, congratulations!!
Just as once upon a time there was a competition for the smallest unit-distance graph of girth 4 on the pages of “Geombinatorics” quarterly, I am inviting your submissions to “Geombinatorics” of record unit-distance graphs of chromatic numbers 5, 6, and 7.
One day, these constructions will enter the second edition of “The Mathematical Coloring Book.” I conjectured there that CNP = 7, and the chromatic number of E^n is 2^(n+1) – 1.
Alexander Soifer
A related question. Can we make any statements about the minimum degree of extension of necessary to support a unit-length graph with chromatic number 5? If I’m not mistaken, we have H lying in
necessary to support a unit-length graph with chromatic number 5? If I’m not mistaken, we have H lying in ![\mathbb{Q}[\sqrt{3}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Csqrt%7B3%7D%5D&bg=ffffff&fg=303030&s=0&c=20201002) , the Moser spindle, V, W, and M all lying in
, the Moser spindle, V, W, and M all lying in ![\mathbb{Q}[\sqrt{3}, \sqrt{13}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Csqrt%7B3%7D%2C+%5Csqrt%7B13%7D%5D&bg=ffffff&fg=303030&s=0&c=20201002) , and the current winner G2 lying in
, and the current winner G2 lying in ![\mathbb{Q}[\sqrt{3}, \sqrt{13}, \sqrt{15}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Csqrt%7B3%7D%2C+%5Csqrt%7B13%7D%2C+%5Csqrt%7B15%7D%5D&bg=ffffff&fg=303030&s=0&c=20201002) . So a degree-8 extension (or 3 successive quadratic extensions, which is probably more relevant). Can we do better or can we prove that this is minimal?
. So a degree-8 extension (or 3 successive quadratic extensions, which is probably more relevant). Can we do better or can we prove that this is minimal?
Sorry, that last one should be $$\mattbb{Q}[\sqrt{3}, \sqrt{13}, \sqrt{15}]$
[Fixed. To use math mode, put “latex ” (with a space after, not before) immediately after the first dollar sign. – M.]
I like this approach. From the looks of Marijn’s .vtx file, G2 and G3 lie in $$\mathbb{Q}[\sqrt{3}, \sqrt{5}, \sqrt{11}]$$. It might be useful to specify a normal form for vertex coordinates. For example, for an extension of a certain degree, coordinates can be represented simply as a pair of tuples of that degree. This might be easier to collaborate with than Mathematica’s reduced form in the .vtx files, and include the coordinate information excluded from the .edge files.
This might also allow some new ways of brute forcing a solution, for example by starting with all points within some distance of the origin in some extension, and then reducing from there.
(Sorry for the errors in my last comment, here’s a corrected version, please delete the previous one.) necessary to, as you phrase it, support a unit-distance graph with chromatic number
necessary to, as you phrase it, support a unit-distance graph with chromatic number 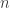 using the following results:
using the following results: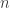 must have a subgraph in which each vertex has degree at least
must have a subgraph in which each vertex has degree at least 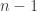 .
. and
and 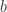 are linearly independent over
are linearly independent over  , then
, then  and
and  are algebraically independent over
are algebraically independent over  . The connection to our problem is as follows: Let
. The connection to our problem is as follows: Let 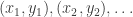 be the vertices of a graph
be the vertices of a graph 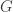 in a drawing of
in a drawing of 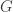 with edges all straight line segments of length 1. Identify the points with the complex numbers
with edges all straight line segments of length 1. Identify the points with the complex numbers 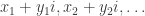 . If the
. If the  and
and  all belong to a field extension
all belong to a field extension 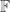 of
of  of degree
of degree 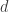 , then the
, then the 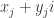 all belong to
all belong to  and hence to a field extension of
and hence to a field extension of  of degree
of degree  . Suppose
. Suppose 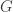 has chromatic number
has chromatic number 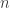 . Let
. Let 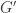 by a subgraph of
by a subgraph of 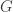 with minimum degree
with minimum degree  . In the drawing of
. In the drawing of 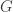 , let
, let  be a vertex that is a vertex of the convex hull of the vertices of
be a vertex that is a vertex of the convex hull of the vertices of 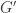 , let
, let  be
be 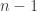 of its neighbours in
of its neighbours in 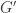 , and let these variables also denote the corresponding complex numbers. Then the
, and let these variables also denote the corresponding complex numbers. Then the 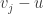 must all be of the form
must all be of the form 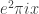 for real
for real  , since they all have absolute value 1. In fact, since they are algebraic, the Lindemann-Weierstrass theorem tells us that they must be of the form
, since they all have absolute value 1. In fact, since they are algebraic, the Lindemann-Weierstrass theorem tells us that they must be of the form 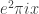 for rational
for rational  . Hence each
. Hence each 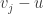 is a
is a 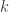 -th root of unity for some
-th root of unity for some 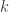 , and the fact that there are
, and the fact that there are 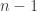 distinct
distinct 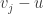 gives us a lower bound for the corresponding
gives us a lower bound for the corresponding 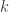 , and hence for the degree of the
, and hence for the degree of the 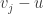 .
.
I think you can lower-bound the minimum degree of extension of
1. A graph with chromatic number
2. The Lindemann-Weierstrass theorem: If
The usual proof that the chromatic number of the plane’s unit distance graph is at most 7 uses a hexagonal tiling.
This upper bound can also be shown by taking a square (or rectangular) tiling, and then shifting each successive row of tiles.
I wonder if the number 6197 given in Dan Pritikin’s nice paper (as a lower bound for the size of a seven- but not six-colorable unit distance planar graph) could be improved by replacing his heptagonal+diamond tiling (which is just a modified hexagonal tiling) with a modification of the usual (or shifted) square tiling. Or maybe a modified pentagonal tiling would do the trick.
The following comment was posted by @dsp:
I think you can lower-bound the minimum degree of extension of necessary to, as you phrase it, support a unit-distance graph with chromatic number
necessary to, as you phrase it, support a unit-distance graph with chromatic number 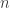 using the following results:
using the following results: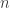 must have a subgraph in which each vertex has degree at least
must have a subgraph in which each vertex has degree at least 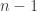 .
. and
and 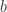 are linearly independent over
are linearly independent over  , then
, then  and
and  are algebraically independent over
are algebraically independent over  . The connection to our problem is as follows: Let
. The connection to our problem is as follows: Let 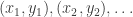 be the vertices of a graph
be the vertices of a graph 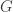 in a drawing of
in a drawing of 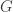 with edges all straight line segments of length 1. Identify the points with the complex numbers
with edges all straight line segments of length 1. Identify the points with the complex numbers 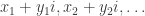 . If the
. If the  and
and  all belong to a field extension
all belong to a field extension 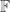 of
of  of degree
of degree 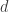 , then the
, then the 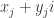 all belong to
all belong to  and hence to a field extension of
and hence to a field extension of  of degree
of degree  . Suppose
. Suppose 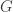 has chromatic number
has chromatic number 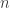 . Let
. Let 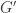 by a subgraph of
by a subgraph of 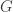 with minimum degree
with minimum degree  . In the drawing of
. In the drawing of 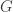 , let
, let  be a vertex that is a vertex of the convex hull of the vertices of
be a vertex that is a vertex of the convex hull of the vertices of 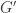 , let
, let  be
be 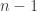 of its neighbours in
of its neighbours in 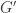 , and let these variables also denote the corresponding complex numbers. Then the
, and let these variables also denote the corresponding complex numbers. Then the 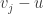 must all be of the form
must all be of the form 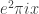 for real
for real  , since they all have absolute value 1. In fact, since they are algebraic, the Lindemann-Weierstrass theorem tells us that they must be of the form
, since they all have absolute value 1. In fact, since they are algebraic, the Lindemann-Weierstrass theorem tells us that they must be of the form 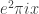 for rational
for rational  . Hence each
. Hence each 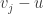 is a
is a 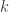 -th root of unity for some
-th root of unity for some 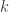 , and the fact that there are
, and the fact that there are 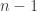 distinct
distinct 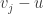 gives us a lower bound for the corresponding
gives us a lower bound for the corresponding 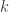 , and hence for the degree of the
, and hence for the degree of the 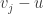 .
.
1. A graph with chromatic number
2. The Lindemann-Weierstrass theorem: If
I see I overlooked another mistake: In my previous comment,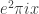 should of course read
should of course read 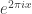 .
.
Can you explain how you are using the fact that is a vertex of the convex hull? I’m probably confused, but it seems to me you are saying that the number
is a vertex of the convex hull? I’m probably confused, but it seems to me you are saying that the number 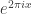 is algebraic if and only if it is a root of unity, which I think isn’t the case.
is algebraic if and only if it is a root of unity, which I think isn’t the case.
Now I’m confused, though you are probably right. But isn’t it true that if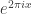 isn’t a root of unity,
isn’t a root of unity,  must be irrational, i. e., linearly independent of 1 over
must be irrational, i. e., linearly independent of 1 over  , which implies by the Lindemann-Weierstrass theorem that
, which implies by the Lindemann-Weierstrass theorem that 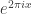 is algebraically independent of
is algebraically independent of 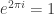 ?
?
The thing with the convex hull isn’t used at all, it’s a remnant of a longer draft of the comment that did use this fact, and should have been deleted when I was editing it. My mistake.
The Lindemann–Weierstrass Theorem actually says: if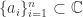 are algebraic numbers which are linearly independent over
are algebraic numbers which are linearly independent over  then
then  are algebraically independent.
are algebraically independent.
The problem is that is not algebraic.
is not algebraic.
(cross-posted for polymathprojects.org; sorry for double-posting) I wonder if all possible 5-colourings of the original and newly constructed graphs can be classified in a certain way? As far as I understand the fact that the original Aubrey de Grey’s verification algorithm for 4-colourings terminates rather quickly indicates that the total number of colourings is not very large? It would be of course desirable then to find subgraphs which are forced to be coloured in a small possible number of ways (modulo obvious symmetries), like the hegaxon for the case of four colours.
One way to gain insight into the possible 5-colorings might be to find simple ways to eliminate all 5-colorings: add a small number of NON-unit-length edges and nodes to a 5-colorable graph Gi until it is no longer 5-colorable. This is sort of the reverse of Marijn’s probing method. The nodes that get used by a successful reverse-probing were likely already highly “entangled” in Gi, and can be focused on when combining Gi’s to look for a non-5-colorable graph.
For example, in an ideal situation where a single non-unit-length edge can be added to a graph G to increase it’s chromaticity, we can use the same copy-and-rotate trick used by the moser spindle and G2/3. This is clearly an ideal situation, but a level of how “entangled” a graph is can be given by how much reverse-probing is required.
Hans Parshall and I went through Falconer’s proof that the measurable chromatic number of the plane (MCNP) is at least 5. It appears as though a proof that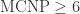 might be within reach by somehow replacing the diamond graph with (a subgraph of) de Grey’s graph.
might be within reach by somehow replacing the diamond graph with (a subgraph of) de Grey’s graph.
What we need is a unit-distance graph G with vertices x and w that satisfy both of the following:
(1) x and w have distance r such that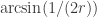 is an irrational multiple of
is an irrational multiple of  .
.
(2) Consider the graph G’ obtained by making a copy x’ of x with the same neighborhood as x. (G’ need not be unit-distance.) For every proper 5-coloring of G’ in which x and x’ receive colors 1 and 2, respectively, then w receives either color 1 or 2.
Presumably, (1) is easy to satisfy since distances are algebraic. Is there a straightforward way to find x and w satisfying (2)? Of course, (2) can be tested for a fixed x and w with a SAT solver, but searching for a good x and w might be a pain…
Might be a naive question, but is there any way to extract any additional property for colorings of previously found non-4-colorable graphs, maybe using computer? Given that only two copies of M can force the chromatic number to be 5, I think it could be possible that we can find additional properties of colorings of previously found graphs with the help of computers.
A property would be, for example, something like: at least two of points A, B, C of a 4-coloring of G should share the same color. At least two of three edges of G of same length has same color, etc.
That first property you mention could be detected by the reverse-probing method I described. If adding a triangle of non-unit-length edges {(A, B), (B, C), (C, A)} to an n-colorable graph G yields a non-n-colorable graph G’, then at least 2 of {A, B, C} share the same color in all n-colorings of G.
I wrote a small Python script, that reads a list of vertices in Mathematica format and embeds the graph into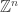 so that each unit-distance vector present in the graph corresponds to a small vector in
so that each unit-distance vector present in the graph corresponds to a small vector in 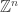 .
.
My main motivation was that working with integer vectors is much easier, especially outside of a computer algebra system. It might also reveal some structure, but I haven’t really looked for that yet.
The code and the output for Marijn’s 826 vertex graph (embedded into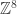 ) can be found at: https://files.jixco.de/pm16/zzvtx/
) can be found at: https://files.jixco.de/pm16/zzvtx/
It requires Python >=3.5, numpy and the fplll command line tool for lattice reduction.
The .basis file contains the vectors needed to map back from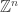 to
to ![\mathbb Q[\ldots]^2](https://s0.wp.com/latex.php?latex=%5Cmathbb+Q%5B%5Cldots%5D%5E2&bg=ffffff&fg=303030&s=0&c=20201002) . The .unit file contains the
. The .unit file contains the 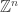 representation of the unit-distance vectors. (i.e. as multiples of the vectors in the .basis file). Finally the .zzvtx file contains the
representation of the unit-distance vectors. (i.e. as multiples of the vectors in the .basis file). Finally the .zzvtx file contains the 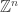 representation of the vertices.
representation of the vertices.
It also contains an example script that takes the output of the zzvtx.py script and generates an edge list in DIMACS format, which I’ve used among other tests to check my code.
I’m not sure if this is the right place to put this, but I have a proposed algorithm for constructing a graph that is not 5-colorable (if such a graph exists). It could also be used to find a graph that is not 4-colorable, but it will probably construct something enormous, so not of direct use to the precise goal of this project. My guess is that if there is a non-5-colorable graph then it is too large to write down unless it has a special structure, so that’s what we aim for.
First some background. A root-3 triangle (RT) is an equilateral triangle of edge-length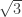 . Aubrey finds two graphs,
. Aubrey finds two graphs, 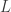 and
and 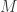 .
. 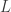 can be 4-colored, but only if it has a monochromatic RT (MRT) as a subset of its vertices.
can be 4-colored, but only if it has a monochromatic RT (MRT) as a subset of its vertices. 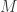 can be 4-colored, but
can be 4-colored, but 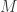 contains a specific RT which cannot be an MRT in any 4-coloring of
contains a specific RT which cannot be an MRT in any 4-coloring of 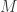 . So we impose
. So we impose 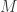 on top of every RT in
on top of every RT in 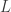 to construct a graph (which we might call
to construct a graph (which we might call 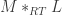 ) with no 4-coloring. Actually, Aubrey doesn’t need to hit every RT in
) with no 4-coloring. Actually, Aubrey doesn’t need to hit every RT in 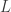 , but it does no harm if we don’t care about the eventual size of the graph.
, but it does no harm if we don’t care about the eventual size of the graph.
Let’s try to abstract this and then generalize it. Fix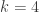 or 5. A configuration is a geometric arrangement of points (for example, an RT). We have a graph
or 5. A configuration is a geometric arrangement of points (for example, an RT). We have a graph 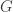 , a configuration
, a configuration 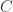 . and a set
. and a set  of
of 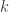 -colorings of
-colorings of 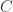 (for example, the four MRT
(for example, the four MRT 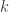 -colorings of an RT). Every
-colorings of an RT). Every 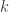 -coloring of
-coloring of 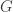 induces an
induces an  -coloring (meaning a coloring which is in
-coloring (meaning a coloring which is in  ) on some
) on some 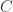 in
in 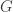 .
.  contains a specific
contains a specific 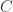 , and every
, and every 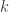 -coloring of
-coloring of  induces a non-
induces a non- coloring of that
coloring of that 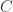 . Build the graph
. Build the graph 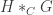 which puts an
which puts an  on every
on every 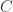 in
in 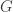 and we’re done.
and we’re done.
Now let’s generalize this idea. Firstly, we don’t need to restrict to a single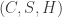 . Suppose we have a collection of configurations
. Suppose we have a collection of configurations 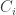 with coloring sets
with coloring sets 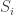 , where every
, where every 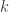 -coloring of G induces some
-coloring of G induces some 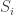 on some
on some 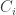 somewhere in G, for some
somewhere in G, for some  . Now suppose we have a collection of
. Now suppose we have a collection of 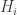 , where each
, where each 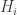 contains a specific
contains a specific 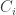 and every
and every 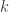 -coloring of
-coloring of 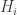 induces a non-
induces a non-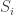 coloring of that
coloring of that 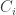 . This will still work, by putting an
. This will still work, by putting an 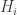 on every
on every 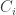 in
in  , for all
, for all  . Let’s regard this as a tree with
. Let’s regard this as a tree with  as the root and
as the root and  as the leaves. This tree has depth 1.
as the leaves. This tree has depth 1.
But we don’t have to stop there. Suppose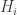 is actually
is actually 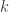 -colorable with an
-colorable with an 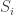 coloring of its
coloring of its 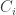 , but suppose there is another configuration
, but suppose there is another configuration 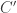 and set of colorings
and set of colorings 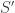 , such that every
, such that every 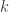 -coloring of
-coloring of 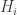 which induces an
which induces an 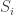 -coloring of its
-coloring of its 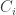 also induces an
also induces an  -coloring of some
-coloring of some  in
in 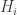 . Now suppose there’s a graph
. Now suppose there’s a graph 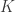 which contains a specific
which contains a specific 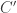 , and every
, and every 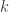 -coloring of
-coloring of 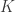 induces a non-
induces a non- coloring of that
coloring of that  . Then we can put
. Then we can put  on every
on every 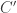 in
in 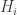 to get
to get 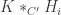 , and we put
, and we put 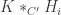 on every
on every 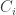 in
in 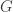 . Of course, we could have used a set
. Of course, we could have used a set 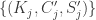 instead of just a single
instead of just a single 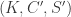 . Also, we could have done this to any of the
. Also, we could have done this to any of the 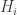 , with in general different sets
, with in general different sets 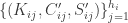 for each
for each 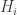 . So this is a tree with depth 2.
. So this is a tree with depth 2.
Clearly there is no limit to the depth of such a tree, except for practical considerations. One advantage of this kind of construction is that it can construct graphs which are very large, and in particular far too large to color if they were not structured, but which we can prove are not colorable.
In practice, the tree might actually be a directed acyclic graph because some of the nodes are the same. The eventual graph is unaffected by this detail, but it might make the representation smaller.
So, how do we go about finding such a thing? Suppose we start with a bag with the property that each
with the property that each 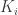 has a specific
has a specific 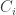 and every
and every 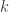 -coloring of
-coloring of 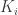 induces a non-
induces a non-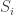 coloring of that
coloring of that 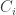 . To start with, the
. To start with, the 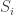 are fairly small sets of colorings. Now we try to combine these. and build a tree from the leaves up. Given a bag
are fairly small sets of colorings. Now we try to combine these. and build a tree from the leaves up. Given a bag 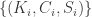 and a graph
and a graph  , we say that a
, we say that a 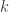 -coloring of
-coloring of  is good if it does not induces an
is good if it does not induces an 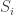 -coloring of any
-coloring of any 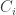 in
in  . Now we’re looking for some
. Now we’re looking for some 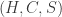 such that
such that  has a specific
has a specific 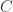 and every good coloring of
and every good coloring of  induces a non-
induces a non- coloring of that
coloring of that 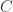 . If we find such an
. If we find such an 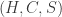 , we can add it to the bag. The point is that we do not need to consider non-good colorings, because we can rule them out later by constructing the appropriate
, we can add it to the bag. The point is that we do not need to consider non-good colorings, because we can rule them out later by constructing the appropriate 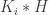 . To recap, as we grow the bag, we only need to consider colorings which do not induce an
. To recap, as we grow the bag, we only need to consider colorings which do not induce an 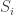 -coloring of any
-coloring of any 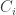 for any
for any  , where
, where 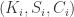 is already in the bag. After we have added
is already in the bag. After we have added 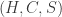 to the bag, we can treat is as just another
to the bag, we can treat is as just another 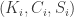 , because this will just increase the depth of the tree. The hope is that eventually we will be able to add a graph with no
, because this will just increase the depth of the tree. The hope is that eventually we will be able to add a graph with no 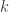 -coloring, and then we’re done.
-coloring, and then we’re done.
Of course, I’m proposing running this with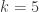 . A nice property of this approach is that we might get an idea of the progress. We can see how the shape of the bag changes with time, and this might give us some idea about whether the project is going to complete or not. We could also start with
. A nice property of this approach is that we might get an idea of the progress. We can see how the shape of the bag changes with time, and this might give us some idea about whether the project is going to complete or not. We could also start with 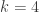 (or even
(or even 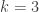 ?) to check the approach. We know that
?) to check the approach. We know that 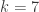 cannot terminate, so that will give an idea of the behavior under conditions where it fails.
cannot terminate, so that will give an idea of the behavior under conditions where it fails.
[Edited. Note that WordPress doesn’t interpret $x$ as math mode unless you include “latex ” with a space after (not before) after the first dollar sign. – M.]
A trivial remark: the unit distance graph in the plane is an example of an infinite abelian Cayley graph, and all of the finite subgraphs of the unit distance graphs can also be viewed as subgraphs of certain finite abelian Cayley graphs. There is a bit of literature on chromatic numbers of abelian Cayley graphs, though from a quick search I didn’t find anything that would make it substantially easier to compute the chromatic number of such graphs as compared to general graphs. Still it might be worth keeping the Cayley graph literature in mind.
I have another alternative construction:
Define V’ by adding to V a rotation of itself by arccos(7/8). It has 60 vertices on the unit circle. We obtain M’ from V’ the same way as in the paper, i.e.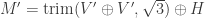 where
where  is the Minkowski sum and
is the Minkowski sum and  removes vertices far from the origin.
removes vertices far from the origin.
The resulting graph M’ is not 4-colourable, even without using L. It seems that we can remove further vertices from V’ and still keep this property.
I played around a bit with constructions similar to this and similar to Marijn’s construction for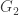 and found this:
and found this:
Starting from the original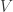 , construct
, construct 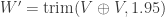 . This is a bit larger than the original
. This is a bit larger than the original  . Next we add a rotation of
. Next we add a rotation of 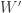 by
by  to itself and call the resulting graph
to itself and call the resulting graph  . The graph
. The graph 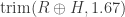 is also not 4-colourable.
is also not 4-colourable.
This construction results in a graph with 2563 vertices (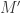 has 7075). I also noticed that it takes a lot longer to check using a SAT solver than
has 7075). I also noticed that it takes a lot longer to check using a SAT solver than 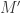 does.
does.
Very nice! Is arccos(7/8) “empirical” or does it come with a reason of why this angle works when other angles fail? Also, is this proper to the Moser spindle? I mean, what about the same type of construction using the Golomb or the “double” Golomb graph as a building block?
It is the angle used for rotation in section 3.3 of the original proof, implicitly occuring as the smallest angle of a triangle with sides 1, 2 and 2. The rotation angle in the Moser spindle is arccos(5/6), which is used in the original V and therefore occurs in V’ as well.
Many thanks Tamas – this is very cool. It presumably works for the same reason as Marijn’s recent constructions, which effectively reduced L to a (1,2,2) triangle. (I still don’t know what that reason is, by the way! – but I’m betting that there is a human-understandable explanation.)
However, there may be much more to it than that. Since the spokes of H are a subset of V and thus of V’, we can view your graph as a subgraph of the Minkowski sum of three copies of V’. Thus, your closing sentence is particularly apposite. How few spokes does a version of V need, in order that the sum of three (four?) copies of it is 5-chromatic? Or, slightly more generally, how few total spokes do three star graphs need in order that their sum is 5-chromatic? This may be a lot more tractable to determine exhaustively than Marijn’s approach of building a large graph and then cutting it down according to the SAT solver’s whim, thus losing symmetry. .It would probably be good to start without any removal of vertices far from the origin. In the first instance presumably we could start by deleting vertices from your V’, but there might also be other promising combinations of angles.
See my reply in the next thread:
Regarding your other question about the Golomb graph, it isn’t that much different as it is constructed with half of the rotation used for the Moser spindle (and a translation). In particular, the examples discussed in this thread with triangular grids and many Moser spindles likely contain a couple of Golomb graphs with side lengths .
.
Visually: https://htamas.ces.hu/files/cnp/mosergolomb/
Many thanks Tamas – that’s a very informative picture. It makes me think that there could be mileage in building out from that graph to make new M’s – there are quite a few pairs of vertices at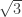 to which diamonds might usefully be added, and I think some of them are at new angles.
to which diamonds might usefully be added, and I think some of them are at new angles.
Let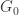 be a graph with chromatic number
be a graph with chromatic number 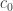 and vertexes
and vertexes 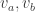 such that
such that 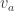 and
and 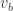 do not not the same color for any
do not not the same color for any 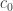 -coloring of
-coloring of 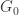 .
. 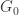 can then be used as a `virtual edge’ with distance
can then be used as a `virtual edge’ with distance  . Let the chromatic color of a virtual edge be defined as the chromatic color of the graph used to virtualize the edge.
. Let the chromatic color of a virtual edge be defined as the chromatic color of the graph used to virtualize the edge.
Multiplicative property of virtual edges:
Let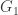 be a graph with chromatic number
be a graph with chromatic number  which virtualizes an edge length
which virtualizes an edge length  . Then replacing all edges of
. Then replacing all edges of  with virtual edges of length
with virtual edges of length  produces a virtual edge of chromatic color
produces a virtual edge of chromatic color 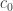 with length
with length 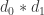 .
.
If a graph,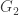 , with chromatic number
, with chromatic number 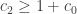 is created using virtual edges with chromatic number
is created using virtual edges with chromatic number 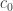 , then a graph,
, then a graph, 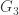 , of chromatic number
, of chromatic number 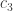 (s.t.
(s.t. 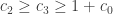 ) can be created by replacing the virtual edges with the graphs which virtualize the virtual edges.
) can be created by replacing the virtual edges with the graphs which virtualize the virtual edges.
More trivially, if a graph,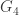 , with chromatic number
, with chromatic number 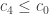 is created using virtual edges with chromatic number
is created using virtual edges with chromatic number  , then replacing the virtual edges with the graphs which virtualize the virtual edges produces a graph with chromatic number
, then replacing the virtual edges with the graphs which virtualize the virtual edges produces a graph with chromatic number  .
.
If virtual edges with chromatic number 4 are found, then they may be useful to make a graph of chromatic number 5 which uses fewer vertexes than the current smallest graph. In an extreme example, 5 vertices would be enough if each of the distances between pairs of vertices corresponds to a virtual edge with chromatic number 4.
Right. However, I don’t know of any unit-distance graph in which two specific vertices V,W are always different colours in any 4-colouring. There are certain distances VW for such (hypothetical) graphs that would give rise to a 5-chromatic graph directly; the only two I know are phi (which works by attaching five copies to a unit-edge regular pentagon) and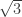 , which works using four copies on the nine-vertex graph formed by spindling two half-hexagons at distance 2. Hm, I wonder if THAT explains why Marijn’s and Tamas’s recent constructions work…
, which works using four copies on the nine-vertex graph formed by spindling two half-hexagons at distance 2. Hm, I wonder if THAT explains why Marijn’s and Tamas’s recent constructions work…
More than 1 virtual edge can be used in the same graph, so for arbitrarily placed points, 10 edges need to be virtualized. E.g. the set of virtual edges {2,3,4} would work for 5 vertexes in a line, and because 4=2*2, the set {2,3} works too.
I just noticed how to make virtual edges of chromatic number 2: a single loop with an even number of nodes. every node an odd number of nodes away is a virtual edge of chromatic number 2.
For virtual edges of chromatic number 3, any distance between points of different colors on the equilateral triangle tiling of the plane.
Virtual edges of chromatic number 4 are easy to create in 3 dimensions using normal tetrahedrons. E.g.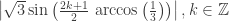 are all valid virtual edges. As for within 2 dimensions, maybe some combination of Moser Spindles could work, though I do not yet see how.
are all valid virtual edges. As for within 2 dimensions, maybe some combination of Moser Spindles could work, though I do not yet see how.
I just noticed a flaw in my previous argument: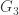 may require more colors than predicted due to overlapping nodes of the graphs which virtualize virtual edges. Luckily this is not a problem for a lower bound argument. This would not be a problem with finite graphs of more than 2 dimensions because the virtual edge graph could be rotated to some arbitrary angle without overlap.
may require more colors than predicted due to overlapping nodes of the graphs which virtualize virtual edges. Luckily this is not a problem for a lower bound argument. This would not be a problem with finite graphs of more than 2 dimensions because the virtual edge graph could be rotated to some arbitrary angle without overlap.
I continued trying variations of the Minkowski sum of star graphs construction:
The star graphs used are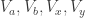 and
and  , which all have a 6-fold rotational symmetry. The graphs
, which all have a 6-fold rotational symmetry. The graphs  and
and 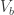 are 25-vertex graphs and
are 25-vertex graphs and 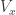 and
and 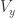 are 13-vertex subgraphs of
are 13-vertex subgraphs of  and
and 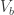 . The graphs
. The graphs 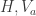 and
and 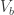 are, apart from the central vertex, pairwise disjoint. The coordinates and drawings can be found at https://files.jixco.de/pm16/stars/
are, apart from the central vertex, pairwise disjoint. The coordinates and drawings can be found at https://files.jixco.de/pm16/stars/
The union of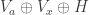 and
and 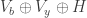 , is a 3085-vertex unit-distance graph that is not 4-colorable. The resulting graph can be trimmed with radius 1.95, giving a 2653-vertex graph that is also not 4-colorable.
, is a 3085-vertex unit-distance graph that is not 4-colorable. The resulting graph can be trimmed with radius 1.95, giving a 2653-vertex graph that is also not 4-colorable.
Great job Jannis. Are you able to eliminate any ranges of distance less than 1.95? When I was shrinking my original graph S, I was able to make a fair bit more progress in that way, over and above shrinking the maximum radius.
I haven’t tried that yet, but will do so now. I also just noticed that I trimmed before adding in H. For trimming the final graph 1.95 is a too small radius.
I also uploaded the resulting graphs to https://files.jixco.de/pm16/stars/
I was able to get it down to 1951 by trimming various ranges before and after adding H (just uploaded the resulting graph).
I’m thinking about shrinking the graph using a SAT solver while keeping the 6-fold symmetry as a next step.
How are you able to rapidly inform us that some graph with 1000s of vertices is not 4-colorable? I just wrote a graph-coloring program and it gets pretty damn slow
somewhere around 30 to 200 vertices, depending on the graph.
I’m using a SAT solver with this script https://files.jixco.de/pm16/edge2cnf.py to convert a DIMACS edge list into a CNF formula (forcing up to 3 suitable vertices to a fixed color, to break some symmetries).
I’m also using different strategies that break more symmetries and split the problem into multiple subproblems, but I always use this simple approach in the end for verification. It takes less than 30 seconds to verify one of the graphs I posted.
Great. Here’s a thought: try trimming based on distance not from the origin but from a point distance 1 from the origin on the line of symmetry of your graph. That will be a way to reproduce Marijn’s construction while also maintaining symmetry about that line. The fact that Marijn got so much further than you have got so far may suggest than one can delete a lot of material on “one side” of your graph.
The way I shrunk the star graphs results in a final graph that has no line of symmetry. This also seems to be essential for being able to remove that many spokes.
Your suggestion lead me to look at mirror symmetries in the intermediate graphs though (I’m just realizing this might have been what you meant?). I noticed that is mirror symmetric, while
is mirror symmetric, while 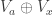 isn’t. And in this case it is possible to fix it without changing the number of spokes. I uploaded a different subgraph of
isn’t. And in this case it is possible to fix it without changing the number of spokes. I uploaded a different subgraph of  , the graph
, the graph 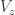 , which replaces
, which replaces 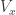 . Unlike
. Unlike 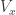 , it shares a line of symmetry with
, it shares a line of symmetry with  .
.
The union of and
and  already has no mirror symmetry, as they don’t share a line of symmetry and are not related by reflection.
already has no mirror symmetry, as they don’t share a line of symmetry and are not related by reflection.
Replacing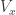 with
with 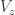 also slightly reduced the (untrimmed) number of vertices from 3085 to 3049.
also slightly reduced the (untrimmed) number of vertices from 3085 to 3049.
By improving the heuristics, the random probing approach found an even smaller unit-distance graph with chromatic number 5. This one has 803 vertices and 4144 edges. The graph is available here:
* http://www.cs.utexas.edu/~marijn/CNP/803.vtx
* http://www.cs.utexas.edu/~marijn/CNP/803.edge
Visualizations based on a 5-coloring of this graph are here:
* http://www.cs.utexas.edu/~marijn/CNP/803.pdf
* http://www.cs.utexas.edu/~marijn/CNP/803black.png
Similar files of the prior records (the ones with 826 and 874 vertices) are stored at that location as well: Simply replace 803 in the links above to either 826 or 874 to access them.
Way to go! I’d recommend putting this on the second (active) thread.
Also: please test Dustin’s hypothesis about moderation, by using more conventional file names, e.g. “803vtx.txt” rather than “803.vtx”.. Great job on the new record!