This is the second “research” thread of the Polymath16 project to make progress on the Hadwiger–Nelson problem, continuing this post. This project is a follow-up to Aubrey de Grey’s breakthrough result that the chromatic number of the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki page.
What follows is a summary of the progress made thus far:
Simplifying de Grey’s graph. There have been three strides along these lines. One is to decrease the size of the graph by iteratively removing vertices that are not necessary to be 5-chromatic. This approach has led to our current record holder, which has 826 vertices and 4273 edges. Another approach has been to hunt for more symmetric 5-chromatic graphs, in the hopes that such graphs might be easier to analyze by hand (e.g., see this and that). Finally, others have been hunting for extremely small alternatives to de Grey’s L and M graphs that are amenable to by-hand analysis, in the hopes that these would eventually lead to a 5-chromatic graph (e.g., see this and that).
Fundamental limits. In 1998, Pritikin proved that every graph with at most 12 vertices is 4-colorable, and every graph with at most 6197 vertices is 6-colorable. Pritikin’s bounds are obtained by coloring the plane with k colors and an additional “wild” color such that points of unit distance are both allowed to receive the wild color. If the wild color occupies a small fraction p of the plane, then an exercise in the probabilistic method gives that any fixed unit-distance graph with n vertices enjoys an embedding in the plane that avoids the wild color (and is therefore k-colorable) provided n<1/p. Pritikin’s coloring for the k=4 case cannot be improved without improving on the densest known subset of the plane that avoids unit distances (originally due to Croft in 1967). See this MO thread for additional information. As such, improving the bound in the k=4 case might require a new technique, whereas the k=5 and 6 cases might be amenable to optimization.
Larger k. Can we use de Grey’s graph to construct unit-distance graphs that are not 5-colorable? To answer this question, we first need to understand how 5-colorings of de Grey’s graph force small collections of vertices to be colored. Varga and Nazgand provide some thoughts along these lines. Even if we can’t stitch together a 6-chromatic unit-distance graph with these ideas, we might be able to apply them to prove that the measurable chromatic number of the plane is at least 6.
Vertices with algebraic structure. It appears as though the coordinates of our smallest 5-chromatic graph lie in (see this). If we view the plane as the complex plane, what is the smallest ring that admits a 5-chromatic single-distance graph? Every single-distance graph in the Eistenstein integers and Gaussian integers is 2-chromatic (see this). David Speyer suggests looking at
next.
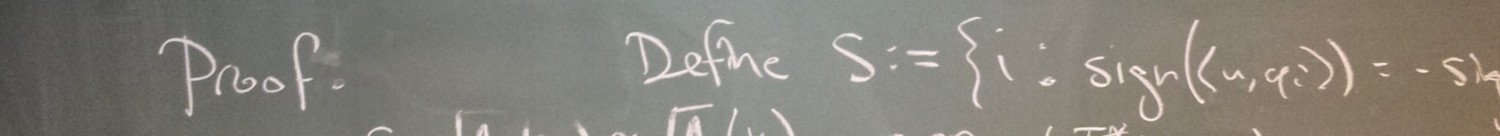
A couple days ago David Speyer asked about the chromatic number of random regular graphs. The statistical physics analysis (which has a 99.9% chance of being correct) is here: https://arxiv.org/pdf/0704.1269.pdf
See the table on page 16. In short:
. A random 5-regular graph is 3-colorable with high probability; a random 6-regular graph is not.
. A random 9-regular graph is 4-colorable with high probability; a random 10-regular graph is not.
. A random 14-regular graph is 5-colorable with high probability; a random 15-regular graph is not.
. A random 19-regular graph is 6-colorable with high probability; a random 20-regular graph is not.
. A random 24-regular graph is 7-colorable with high probability; a random 25-regular graph is not.
For sufficiently large k, results of this nature are proven (see arxiv.org/pdf/1308.4287.pdf). I think the transitional degree is basically between the floor and ceiling of (2k-1)ln(k)-1.
Let me make the following simple observation.
In order for a graph to be k-chromatic and minimal
it must be (k-1)-connected. In other words: removing k-2 vertices
cannot disconnect the graph.
Why should we care? Because computing the chromatic number k of a graph
(if k>=3) is NP-hard. But for any fixed k, it is polynomial time to
decide if graph is k-connected (and find a cutset if not).
Therefore, we can efficiently “prune” a graph, to produce a smaller one
that also works. Marijn Huele did such pruning
using his insane “DRAT trim” software tools applied to a SAT problem
solver’s proof. All that was NP-hard.
That was admirable, but for those of us who do not have such fancy software and want to remain in polynomial time, you can try this instead.
Regarding the comment about software, please note that Marijn’s DRAT-trim is open source (as are many SAT solvers): https://www.cs.utexas.edu/~marijn/drat-trim/
It can directly produce a reduced core, i.e. an unsatisfiable subset of the input formula. For most encodings it is easy to transform that back into a subgraph. (E.g. in the encoding I linked in an earlier comment generates a 4-literal clause for each vertex. A missing clause in the core is a vertex that can be removed.)
Thanks for rolling over the thread and for the great summary!
I have been trying to update the wiki with various progress from the previous thread, but there may be inaccuracies, particularly in the description of some of the new graphs being created. Please feel free to update the wiki directly (you may have to request an account from Michael Nielsen to have edit access though).
For the symmetry track (reply to Aubrey’s April 20 7:08 comment in the first thread):
Let .
.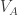 with 36 points.
with 36 points.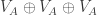 is not 4-colourable.
is not 4-colourable.
Unit vectors with angles from A define a set
The Minkowski sum
That’s great! I think that’s the shortest description length we have for a 5-chromatic example?
Lovely! It will be very interesting to see how much this can be trimmed.
Tamas – I suggest to build your graph using j in {-1/2, 0, 1/2} and k in {-1/2, 1/2} so that it has mirror symmetry about the x-axis. (I think that’s the same graph, yes?) Then we can try my suggested test for trimming based on distance from (1,0).
Oops, I commented with the wrong account. Can someone delete my comment? Thanks
Given a set of unit-vectors like A, we can “search” the plane starting at the origin, with movements along unit vectors, adding explored points to a graph. V_A corresponds to an exhaustive search of all nodes up to depth 3. We could instead “search” with a heuristic: repeatedly add the point that would add the most edges to previously added points.
When the set of unit-vectors is the 6 in H, this spirals out to generate the Eisenstein integers. When the set is A, I get a strange growing shape, but my code might be buggy or require modification. I’m curious if this process would eventually generate a non-4-colorable graph, and how many points would be required.
Some pictures and Mathematica code: https://drive.google.com/drive/folders/1jvfjLX-lazSs63AL_MaXprZq8mpdYd7Q
There seems to be symmetry along the line x = y. Does rotation clockwise by pi/4 simplify anything?
I was wondering why you allow for j=1/2, and I realized that this half angle naturally appears in the Moser spindle:
As such, you are introducing Moser spindles at multiple orientations. This is exactly what Aubrey had in mind when designing U in his Figure 6. You also mentioned a relationship to Golomb’s graph in the previous thread:
I was confused by the different scales at play in your picture, but I was able to identify how these differently oriented spindles conspire to produce Golomb’s graph:
Here, we spindle about A to get the moves labeled “1”, etc. Overall, I think we can capture the j=1/2 rotations by throwing in yet another Minkowski sum.
Wow, that’s a much nicer Moser-Golomb construction than mine.
Indeed, we can generate a non-4-colourable graph without the j=1/2 rotations by replacing them with four other unit vectors as in the Moser spindle. It follows that a 12-fold Minkowski sum would suffice. However, I’ve checked up to 7-fold Minkowski sums and they are still 4-colourable.
(By the way, if anyone is interested in pushing this direction, the 8-fold sum is available in dimacs format here: https://htamas.ces.hu/files/cnp/v24p8.sat.xz . Warning: It decompresses to 1.4 GB and will require a machine with at least 16GB of memory.)
Ah, so if we were to use a similar group to shoot for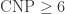 , we would likely save a lot of computation by identifying all unit vectors in the group before taking Minkowski sums.
, we would likely save a lot of computation by identifying all unit vectors in the group before taking Minkowski sums.
Observe that spindles to produce a (2,2,1)-triangle. The unit leg of one of these triangles is at angle
spindles to produce a (2,2,1)-triangle. The unit leg of one of these triangles is at angle  . If you include this angle in your
. If you include this angle in your 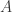 , does
, does 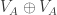 suffice? Or do you still need the 3-fold sum?
suffice? Or do you still need the 3-fold sum?
We still need the 3-fold sum. I also tried to add some further unit vectors from the group, but still no luck. I’m not sure how to enumerate all of them, though.
> I also tried to add some further unit vectors from the group, but still no luck.
Are you saying there are more angles beyond , where
, where 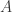 is the list of angles you posted above?
is the list of angles you posted above?
Yes, for instance the angles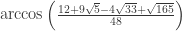 and
and 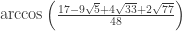 (along with their rotations by
(along with their rotations by 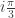 ) can be constructed from the sum of four unit vectors in
) can be constructed from the sum of four unit vectors in 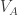 but are not in the set you mentioned.
but are not in the set you mentioned.
I made a typo before simplifying the second expression. They are more symmetric: and
and 
I’ve just uploaded to the dropbox a PNG file of Tamas’s graph, rendered in the style I used in the paper. Rather a large file, but worth it just for the aesthetics 🙂
Ack – apologies to Tamas – I just noticed that the graph I drew and uploaded yesterday had accidentally incorporated a trimming to radius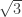 (which is, in fact, 4-colorable). I’ve uploaded a corrected version now (and corrected the vertex and edge counts that I had entered on the wiki).
(which is, in fact, 4-colorable). I’ve uploaded a corrected version now (and corrected the vertex and edge counts that I had entered on the wiki).
In the construction of L there is a triangle with sides 4, 4 and 1. Doesn’t this mean that the ring will also need to be extended with ?
?
Assuming the answer is that this step was eliminated, does that mean the smallest known ring with a five chromatic graph is the integers extended with the three unit complex numbers at the right angles?
Denote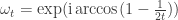 . Then [1] and [2] together indicate that
. Then [1] and [2] together indicate that ![\mathbb{Z}[\omega_1,\omega_3,\omega_4]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Comega_1%2C%5Comega_3%2C%5Comega_4%5D&bg=ffffff&fg=303030&s=0&c=20201002) is not 4-colorable. This is the smallest ring we have that admits a 5-chromatic unit-distance graph. Observe that
is not 4-colorable. This is the smallest ring we have that admits a 5-chromatic unit-distance graph. Observe that  spindles the hex lattice to form a
spindles the hex lattice to form a  -triangle. For example,
-triangle. For example, 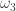 provides the rotation needed for a Moser spindle. For this reason, [3] suggests considering all
provides the rotation needed for a Moser spindle. For this reason, [3] suggests considering all  for which
for which  is the squared norm of some nonzero member of the hex lattice (listed in [4]). As you point out, the multiplicative structure is perhaps overkill, since we only use the additive group generated by
is the squared norm of some nonzero member of the hex lattice (listed in [4]). As you point out, the multiplicative structure is perhaps overkill, since we only use the additive group generated by  .
.
Apologies if I am just catching up and repeating known stuff.
The emerging strategy seems to be to start with an additive group of complex numbers which includes some units. It may be part of a ring but it is the additive part that matters most. We want examples with some linear relationships between the units with small integer coefficients.
If there is a homomorphism to a small finite abelian group such that no unit is mapped to the identity then it can be coloured with that group, so you look for examples where this is not possible for all groups up to order 4 (or 5). I.e. where the relationships between the units rules out all possible homomorphisms.
Then explore with computation or logic whether it has subgraphs that cannot be coloured and find the smallest.
The group of rational complex numbers is bipartite, so we look for extensions over several square roots and small denominators. Has there been any systematic search for other examples?
To echo Phillip Gibbs comment: of we have any understanding of what makes a particular additive group good, beyond not having any lattice colorings and havin a lot of unit vectors?
It might be useful to clarify some terminology so that we can ask some more specific questions. A colouring of an additive group of complex numbers can be a group homomorphism. More generally a colouring can be periodic if for every
can be periodic if for every  in the group there is an integer
in the group there is an integer  such that
such that 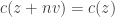 . A homomorphism is always periodic.
. A homomorphism is always periodic.
If a group can be coloured, are there always periodic colourings? Can anything be said about minimum size of the periodicity? Are there examples of groups which have colourings but which do not have colourings that are homomorphisms? Perhaps there is already some better terminology already in use that would be worth stating?
@DavidSpeyer – We don’t have much understanding yet. Given an additive subgroup of , we take its unit vectors as generators, and then we consider the resulting the Cayley graph. I’ve only skimmed the literature on coloring Cayley graphs, but it seems that the main techniques for bounding the chromatic number are to get upper bounds from homomorphic colorings and lower bounds from the standard techniques (Hoffman, Lovasz, inverse independence ratio). Since Cayley graphs are vertex-transitive, the inverse independence ratio equals the fractional chromatic number [1], which is already of interest [2]. However, Frank Vallentin reported to me that de Grey’s 1581-vertex graph has independence number between 509 and 550, resulting in an inverse independence ratio of about 3, which is a far cry from the
, we take its unit vectors as generators, and then we consider the resulting the Cayley graph. I’ve only skimmed the literature on coloring Cayley graphs, but it seems that the main techniques for bounding the chromatic number are to get upper bounds from homomorphic colorings and lower bounds from the standard techniques (Hoffman, Lovasz, inverse independence ratio). Since Cayley graphs are vertex-transitive, the inverse independence ratio equals the fractional chromatic number [1], which is already of interest [2]. However, Frank Vallentin reported to me that de Grey’s 1581-vertex graph has independence number between 509 and 550, resulting in an inverse independence ratio of about 3, which is a far cry from the  we need to prove 5-chromatic. I doubt the Cayley graph that contains de Grey’s will do much better in this regard.
we need to prove 5-chromatic. I doubt the Cayley graph that contains de Grey’s will do much better in this regard.
Here’s another approach that’s reminiscent of de Grey’s original analysis. If a finite abelian Cayley graph is uniquely k-colorable (i.e., every proper k-coloring exhibits the same color classes), then the graph is k-chromatic and the coloring is necessarily homomorphic; see Theorem 2.2 in [3]. (I suspect “finite” is unnecessary here.) For example,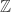 is uniquely 2-colorable, and its color classes are cosets of
is uniquely 2-colorable, and its color classes are cosets of 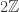 . Since the color at 1 is determined by the color at 0, we can “spindle” by considering
. Since the color at 1 is determined by the color at 0, we can “spindle” by considering  . Then the rotated version of 1 in
. Then the rotated version of 1 in  is also determined by the color at 0, and in particular, it must receive the same color as the original 1, but thanks to the spindle, these two copies of 1 are unit distance apart. As such,
is also determined by the color at 0, and in particular, it must receive the same color as the original 1, but thanks to the spindle, these two copies of 1 are unit distance apart. As such,  , and the additive group
, and the additive group  they generate, is not 2-colorable. Notice that we could have spindled any member of
they generate, is not 2-colorable. Notice that we could have spindled any member of 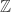 about 0 since its color is similarly determined by the color at 0.
about 0 since its color is similarly determined by the color at 0.
Next, is uniquely 3-colorable. The color classes are cosets of the sublattice generated by the vectors of norm
is uniquely 3-colorable. The color classes are cosets of the sublattice generated by the vectors of norm 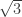 . As such, we can spindle any member
. As such, we can spindle any member  of this sublattice about the origin so that any 3-coloring of the copies of
of this sublattice about the origin so that any 3-coloring of the copies of  in
in  gives the same color to
gives the same color to  and
and 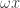 , which are unit distance apart. Thus,
, which are unit distance apart. Thus,  , and the additive group
, and the additive group 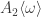 they generate, is not 3-colorable. If
they generate, is not 3-colorable. If  were chosen to have norm
were chosen to have norm 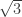 , then
, then 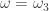 from my previous comment, and
from my previous comment, and  contains the vertices of a Moser spindle.
contains the vertices of a Moser spindle.
Is uniquely 4-colorable? Empirically, its 4-colorings are thwarted by spindling 2 about 0, or at least by completing this spindle move to the additive group
uniquely 4-colorable? Empirically, its 4-colorings are thwarted by spindling 2 about 0, or at least by completing this spindle move to the additive group 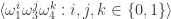 it generates [4]. Understanding this observation seems to be the crux of the problem.
it generates [4]. Understanding this observation seems to be the crux of the problem.
I guess if our additive group is a group of algebraic integers O_K in a number field K (considered as a subfield of C), the elements of length 1 form a (multiplicative) subgroup of the group of units of O_K, which is something we understand pretty well. Somehow I feel like what one must want is a lot of low-height additive relations between these units.
The question Dustin asks is a really nice one: what can we say about the Cayley graph whose vertices are the integers O_K and whose edges correspond to addition of units in O_K^*? (or some subgroup of O_K^*.) Of course, phrased this way, the real numbers drop out entirely, maybe that’s why I find it nice….!
A quibble: The Moser spindle makes use of the point . That is not a unit. Rather, in the UFD
. That is not a unit. Rather, in the UFD ![\mathbb{Z}[\tfrac{1+\sqrt{-11}}{2}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Ctfrac%7B1%2B%5Csqrt%7B-11%7D%7D%7B2%7D%5D&bg=ffffff&fg=303030&s=0&c=20201002) , it factors as
, it factors as  , where
, where  are the primes above (3).
are the primes above (3).
I think I have two inequivalent (though very similar!) 4-colorings of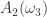 . Let me switch to more number theoretic notation. Let K be the field
. Let me switch to more number theoretic notation. Let K be the field  . If I understand your notation correctly,
. If I understand your notation correctly, 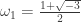 and
and  . Let R be the ring they generate, this is
. Let R be the ring they generate, this is ![\mathcal{O}_K[3^{-1}]](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BO%7D_K%5B3%5E%7B-1%7D%5D&bg=ffffff&fg=303030&s=0&c=20201002) . Both
. Both 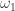 and
and 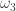 lie on the unit circle so
lie on the unit circle so  does for any exponents a and b. You want to 4-color the graph whose vertices are R and whose edges are elements which differ by
does for any exponents a and b. You want to 4-color the graph whose vertices are R and whose edges are elements which differ by  .
.
As rings, we have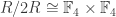 , where
, where  is the ring with 4-elements. If we reduce
is the ring with 4-elements. If we reduce  modulo 2, I get the 9 elements of
modulo 2, I get the 9 elements of  which project to nonzero elements in each factor.
which project to nonzero elements in each factor.
Therefore, either projection to the first or the second factor is a 4-coloring of R.
factor is a 4-coloring of R.
Of course, if these are the only two 4-colorings, that would still be great to know!
This is wrong in detail but right in concept. The element is also a unit vector, and I’m not sure whether or not it is in the group generated by the others. But it still is nonzero under both projections to
is also a unit vector, and I’m not sure whether or not it is in the group generated by the others. But it still is nonzero under both projections to  .
.
Can we show that, in any 4-coloring of R, the elements 0 and 2 get the same color? If so, it follows that the only 4-colorings are the ones I found.
@DavidSpeyer – In fact, if 0 and 2 receive the same color in every 4-coloring, then we are done: Spindling 2 about 0 would force the two copies of to not be simultaneously 4-colorable.
to not be simultaneously 4-colorable.
Now that I think about it, if there is any distance which always separates vertices of the same color in any k-coloring, then it is easy to see the plane is not k-colorable. Let that distance be r. We can find some cycle of points with distances (r,r,r,…,r,1), and we can’t color that.
So, let me ask: Do you think there are 4-colorings of A_2(omega_3) which are not periodic modulo 2 A_2(omega_3)? Do you have any idea what they look like?
@David: unfortunately there are many such colourings. Even if we restrict ourselves to the colourings containing no monochromatic triangles of side-length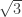 , we have the situation shown in Figure 3 of my paper, in which each horizontal row of vertices features just two colours but there is no restriction on which parity each row has.
, we have the situation shown in Figure 3 of my paper, in which each horizontal row of vertices features just two colours but there is no restriction on which parity each row has.
@Aubrey – David is trying to color , which is two copies of the hex lattice, Moser spindled. Your Figure 3 just looks at 4-colorings of the hex lattice. Spindling should rule out many colorings…?
, which is two copies of the hex lattice, Moser spindled. Your Figure 3 just looks at 4-colorings of the hex lattice. Spindling should rule out many colorings…?
EDIT: is much larger. It’s closer to your M, Aubrey.
is much larger. It’s closer to your M, Aubrey.
First of all, I have to say, I am not a huge fan of Dustin’s notation, and I might be misusing it. I want to color the ring R of numbers of the form
where (a,b,c,d) are integers with a+b+c+d even. The group of length 1 units in this ring is generated by (1+sqrt(-3))/2 and (sqrt(33)+sqrt(-3))/6, and is generated by these two elements. I’ll call these elements omega and eta. The ring elements 0, 1, omega, 1+omega, eta^2, eta^2 omega, eta^2 (1+omega) is a Moser spindle. (If I understand right, omega is Dustin’s omega_1 and eta^2 is omega_3.)
Figure 3 of your paper colors only the subring generated by omega.
Ah yes, my apologies. However, I think what I said is still true. After Marijn found his 800-odd graphs, I spent a little time looking at exactly the spindling of a pair of triangular lattices at distance 2 and was unable to find any clear reason why it is 5-chromatic even when there are no monochromatic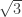 triangles – in other words, I think there is something additional about the original M that forbids a 4-colouring. Thus, when such triangles are allowed, I believe that the flexibility of colouring is really high.
triangles – in other words, I think there is something additional about the original M that forbids a 4-colouring. Thus, when such triangles are allowed, I believe that the flexibility of colouring is really high.
@David I believe your ring can be 4-coloured as follows. Define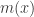 to be a function from
to be a function from  to
to  by the sequence 1,2,1,3,2,3. Colour the unit length complex numbers using
by the sequence 1,2,1,3,2,3. Colour the unit length complex numbers using  . colour all other elements using an additive group homomorphism to
. colour all other elements using an additive group homomorphism to  i.e.
i.e.  To verify that this works you need to check that it is consistent with all additive identities for the units.
To verify that this works you need to check that it is consistent with all additive identities for the units.
@Philip – I’m having difficulty verifying that your coloring satisfies the constraint imposed by the Moser spindle:
Perhaps I’m misinterpreting your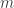 ?
?
I haven’t checked Phillip Gibbs’ specific formula, but he is right that there is a coloring which is periodic for a quotient , which makes it different from mine that uses
, which makes it different from mine that uses  . The quotient ring
. The quotient ring  is isomorphic to
is isomorphic to ![\mathbb{Z}[\omega]/4 \times \mathbb{Z}[\omega]/4](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F4+%5Ctimes++%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F4&bg=ffffff&fg=303030&s=0&c=20201002) . Since 33 has a square root 2-adically, of the form 1+16+…, we have
. Since 33 has a square root 2-adically, of the form 1+16+…, we have 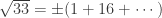 . Also
. Also  . So
. So  is equivalent to
is equivalent to  in one of the
in one of the ![\mathbb{Z}[\omega]/4](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F4&bg=ffffff&fg=303030&s=0&c=20201002) factors and
factors and 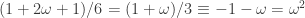 in the other factor.
in the other factor.
So the unit group of maps to the group generated by
maps to the group generated by  in
in ![\mathbb{Z}[\omega]/4 \times \mathbb{Z}[\omega]/4](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F4+%5Ctimes++%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F4&bg=ffffff&fg=303030&s=0&c=20201002) . There are many
. There are many 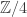 additive quotients of this
additive quotients of this ![\mathbb{Z}[\omega]/4 \times \mathbb{Z}[\omega]/4](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F4+%5Ctimes++%5Cmathbb%7BZ%7D%5B%5Comega%5D%2F4&bg=ffffff&fg=303030&s=0&c=20201002) which do not kill any
which do not kill any  . For example, project onto the first factor and quotient by
. For example, project onto the first factor and quotient by 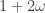 .
.
Thanks for checking, yes it is out by a sign. I hope it can be corrected using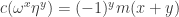 .
.
I am not sure how this would relate to what David wrote, but I imagine there must be some way this translates to a formula in terms of
I wrote a post about Oliveira’s computation of the Lovasz number of the (complement of the) unit-distance graph in R^2; he works in greater generality in his thesis and I thought it might be useful to see concretely just how we can embed R^2 in a Hilbert space in a way that witnesses the smallness of the Lovasz number.
Aubrey has proposed a few methods to trim existing constructions into smaller constructions that still look nice. I wanted to propose an alternative trimming procedure that enjoys a couple of nice properties.
This procedure is specifically designed to trim point sets of the form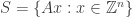 , where
, where 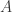 is a real
is a real 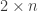 matrix of rank 2 such that
matrix of rank 2 such that 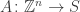 is injective. For example, the point set in [1] comes from taking
is injective. For example, the point set in [1] comes from taking 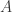 to be the
to be the  matrix whose columns are given by
matrix whose columns are given by  ; see [2]. Let
; see [2]. Let  be any full rank
be any full rank 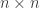 matrix whose first two rows come from
matrix whose first two rows come from 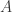 (for example, you can randomly draw the
(for example, you can randomly draw the  submatrix
submatrix 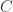 at the bottom of
at the bottom of  with independent Gaussian entries). Then for any fixed
with independent Gaussian entries). Then for any fixed  , define
, define
By assumption, there already exists a finite subset of that is k-chromatic, meaning
that is k-chromatic, meaning  is k-chromatic for some
is k-chromatic for some  . The proposed trimming procedure hunts for the smallest
. The proposed trimming procedure hunts for the smallest  such that
such that  is k-chromatic. In practice, one would only consider points in
is k-chromatic. In practice, one would only consider points in  with small norm.
with small norm.
Here are some nice properties of this procedure:
(a) is a so-called cut-and-project set, and so we are guaranteed that the points in
is a so-called cut-and-project set, and so we are guaranteed that the points in  are well spread out (no two are too close, and there are no large gaps). This is due to Meyer; see Theorem 2.2 in [3].
are well spread out (no two are too close, and there are no large gaps). This is due to Meyer; see Theorem 2.2 in [3].
(b) Since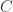 can be generated at random, we can run the procedure multiple times to find a small
can be generated at random, we can run the procedure multiple times to find a small  .
.
In the previous thread, dsp was hoping that quasicrystals could somehow be used to provide upper bounds [4]. They appear to provide lower bounds instead. I have no idea if other properties of quasicrystals (e.g., their Fourier transform) will be of use to us.
Some of the recent discussion has been focusing on finding ring extensions of that are not 4-colorable. As mentioned in the parent post, the current example is a finite subgraph in
that are not 4-colorable. As mentioned in the parent post, the current example is a finite subgraph in ![\mathbb{Q}[i, \sqrt{3}, \sqrt{5}, \sqrt{11}]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5Bi%2C+%5Csqrt%7B3%7D%2C+%5Csqrt%7B5%7D%2C+%5Csqrt%7B11%7D%5D&bg=ffffff&fg=303030&s=0&c=20201002) . I would like to ask a slightly different question:
. I would like to ask a slightly different question:
What is the chromatic number of the unit-distance graph on![\mathbf{Q}[i, \omega_3, \omega_5, \omega_7, \ldots]](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BQ%7D%5Bi%2C+%5Comega_3%2C+%5Comega_5%2C+%5Comega_7%2C+%5Cldots%5D&bg=ffffff&fg=303030&s=0&c=20201002) where
where  is a
is a 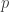 -th root of unity. Algebraically, this is the infinite cyclotomic extension of
-th root of unity. Algebraically, this is the infinite cyclotomic extension of  . Geometrically this is equivalent to the chromatic number of the plane when one restrict all edges to have angles that are rational multiples of
. Geometrically this is equivalent to the chromatic number of the plane when one restrict all edges to have angles that are rational multiples of  as measured from the
as measured from the  -axis.
-axis.
It is unclear to me, at least to me, whether or not this is trivial that the chromatic number of![\mathbf{Q}[i, \omega_3, \omega_5, \omega_7, \ldots]](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BQ%7D%5Bi%2C+%5Comega_3%2C+%5Comega_5%2C+%5Comega_7%2C+%5Cldots%5D&bg=ffffff&fg=303030&s=0&c=20201002) is more than
is more than 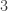 . For example,
. For example, ![\mathbf{Q}[i, \omega_3]](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BQ%7D%5Bi%2C+%5Comega_3%5D&bg=ffffff&fg=303030&s=0&c=20201002) yields a triangular lattice (rather, countable disconnected copies), and it is straight-forward to show that the chromatic number is 3. For example, I suspect that the unit-distance graph on
yields a triangular lattice (rather, countable disconnected copies), and it is straight-forward to show that the chromatic number is 3. For example, I suspect that the unit-distance graph on ![\mathbf{Q}[i, \omega_3, \omega_5, \omega_7]](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BQ%7D%5Bi%2C+%5Comega_3%2C+%5Comega_5%2C+%5Comega_7%5D&bg=ffffff&fg=303030&s=0&c=20201002) has chromatic number at least 4 or 5, but I have no way of verifying that. I have the Hoffman ratio of a subgraph of
has chromatic number at least 4 or 5, but I have no way of verifying that. I have the Hoffman ratio of a subgraph of ![\mathbf{Q}[i, \omega_3, \omega_5, \omega_7]](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BQ%7D%5Bi%2C+%5Comega_3%2C+%5Comega_5%2C+%5Comega_7%5D&bg=ffffff&fg=303030&s=0&c=20201002) is about 2.91, so it seems to indicate that it probably isn’t 3.
is about 2.91, so it seems to indicate that it probably isn’t 3.
I suspect that![\mathbf{Q}[i, \omega_3, \omega_5, \omega_7]](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BQ%7D%5Bi%2C+%5Comega_3%2C+%5Comega_5%2C+%5Comega_7%5D&bg=ffffff&fg=303030&s=0&c=20201002) may be an interesting example to study because is one of the smallest cyclotomic extensions where there are “non-trivial” cycles that cannot be decomposed two smaller “cycles.”
may be an interesting example to study because is one of the smallest cyclotomic extensions where there are “non-trivial” cycles that cannot be decomposed two smaller “cycles.”
Just a thought.
There a length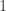 elements in this infinite cyclotomic extension which are not roots of unity. Indeed,
elements in this infinite cyclotomic extension which are not roots of unity. Indeed, 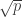 is contained in
is contained in 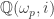 (and you don’t need
(and you don’t need  if
if  ), so all the numbers rings which have been proposed so far are inside cyclotomic fields.
), so all the numbers rings which have been proposed so far are inside cyclotomic fields.
Let me correct my point/question. While it is true that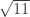 is in the field
is in the field ![\mathbb{Q}[\omega_3, \omega_5, \omega_7, \ldots]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BQ%7D%5B%5Comega_3%2C+%5Comega_5%2C+%5Comega_7%2C+%5Cldots%5D&bg=ffffff&fg=303030&s=0&c=20201002) ,
, ![\sqrt{11} \not\in \mathbb{Z}[i,\omega_3, \omega_5, \omega_7, \omega_9, \ldots]](https://s0.wp.com/latex.php?latex=%5Csqrt%7B11%7D+%5Cnot%5Cin+%5Cmathbb%7BZ%7D%5Bi%2C%5Comega_3%2C+%5Comega_5%2C+%5Comega_7%2C+%5Comega_9%2C+%5Cldots%5D&bg=ffffff&fg=303030&s=0&c=20201002) as a module over
as a module over 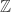 .
.
I would like to ask: What is the chromatic number of the infinite graph where and
and  ?
?
Thus far, none of the examples where the plane is 5-colorable are subgraphs of the graph above. In fact, it is not clear to me if it is obvious whether the graph above requires more than 3 colors.
It seems that we’ve made some steps towards a human proof that . Following Tamás Hubai’s 5-chromatic construction in [1], we’ve turned our attention to a subring
. Following Tamás Hubai’s 5-chromatic construction in [1], we’ve turned our attention to a subring  of
of  described by David Speyer in [2]. If we understand the set of 4-colorings of this ring, then we will able to prove
described by David Speyer in [2]. If we understand the set of 4-colorings of this ring, then we will able to prove  . The set of units in
. The set of units in  with unit modulus form a multiplicative subgroup generated by
with unit modulus form a multiplicative subgroup generated by
and
I want to point out three facts:
(i) Every 4-coloring of forces
forces 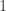 ,
, 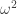 and
and 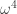 to not receive the same color.
to not receive the same color.
(ii) There exists a human proof that (i) implies .
.
(iii) The current proof of (i) is computer-assisted.
To see this, consider the following modification of Aubrey’s Figure 7(right) in [3]:
This illustrates how the vertices in Aubrey’s can be expressed as a rotation of
can be expressed as a rotation of
(I took the liberty of coloring points according to the value of to help with visualization.) The vertices in Aubrey’s
to help with visualization.) The vertices in Aubrey’s 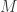 form a subset of
form a subset of  , which can be thought of as a subset of
, which can be thought of as a subset of  by the above correspondence. Furthermore, Aubrey reports that every 4-coloring of
by the above correspondence. Furthermore, Aubrey reports that every 4-coloring of 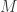 forces
forces 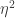 ,
, 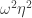 and
and 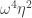 to not receive the same color, implying (i). In fact, Aubrey also reports that
to not receive the same color, implying (i). In fact, Aubrey also reports that 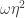 ,
, 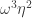 and
and  do not receive the same color, but if we color all of
do not receive the same color, but if we color all of  , this is implied by (i). From (i), a proof of
, this is implied by (i). From (i), a proof of  relies on properties of Aubrey’s
relies on properties of Aubrey’s 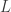 , which can be derived by hand.
, which can be derived by hand.
At the moment, we are focusing on homomorphic colorings of , in which the set of colors is a group
, in which the set of colors is a group 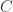 and the coloring function
and the coloring function  is a homomorphism. Homomorphic colorings are nice because they are amenable to by-hand analysis, but (i) is a statement about all colorings. Does every 4-coloring of
is a homomorphism. Homomorphic colorings are nice because they are amenable to by-hand analysis, but (i) is a statement about all colorings. Does every 4-coloring of  produce color classes that come from some homomorphic coloring? The answer would probably be “yes” if
produce color classes that come from some homomorphic coloring? The answer would probably be “yes” if  were uniquely 4-colorable (see [4]), but it doesn’t appear to be. Presumably, this can be tested with the help of a SAT solver.
were uniquely 4-colorable (see [4]), but it doesn’t appear to be. Presumably, this can be tested with the help of a SAT solver.
As an aside, do we know of a finite k for which the entire plane is k-colorable by a homomorphic coloring?
Suppose we have colouring give by a homomorphism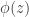 from
from  to
to 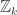 . Let
. Let  be the complex number in the upper half complex plane such that
be the complex number in the upper half complex plane such that 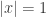 and
and 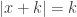 . Then
. Then 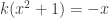 . Therefore
. Therefore 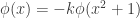 which is congruent to zero mod
which is congruent to zero mod 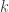 . So
. So  is a unit complex number that maps to zero and any two points separated by this number must have the same colour.
is a unit complex number that maps to zero and any two points separated by this number must have the same colour.
To put it in simpler terms, a graph with points in the form of a triangle with sides
points in the form of a triangle with sides  cannot be coloured with an additive homomorphism onto
cannot be coloured with an additive homomorphism onto 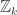 , so homomorphisms are too restrictive, but may still be useful to eliminate options.
, so homomorphisms are too restrictive, but may still be useful to eliminate options.
Ah, in fact, you can replace with any abelian group of order
with any abelian group of order 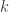 . Thanks!
. Thanks!
It might be useful to work out the homomorphic colourings to for the main ring of interest. That could be a good basis for looking in other directions.
for the main ring of interest. That could be a good basis for looking in other directions.
There are three unit generators of a ring ,
,  and
and 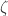 with relations
with relations
We are looking for a mapping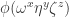 to
to 
The powers of follow a sequence in any ring of the form
follow a sequence in any ring of the form  The solutions mod 5 which avoid zero follow one of two sequences:
The solutions mod 5 which avoid zero follow one of two sequences:
1,2,1,4,3,4 or 3,1,3,2,4,2 up to cyclic permutations. Notice that every pair of distinct non-zero numbers appear in these sequences as consecutive entries.
Consider the mapping for the powers of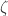 which form a sequence
which form a sequence 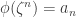 . The equation for
. The equation for 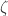 can be transformed mod 5 to
can be transformed mod 5 to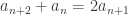 so the sequence must be an arithmetic progression mod 5 which avoids zero, it is therefore a constant.
so the sequence must be an arithmetic progression mod 5 which avoids zero, it is therefore a constant.
give
In general for mapping to other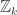 this equation is a problem when
this equation is a problem when 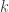 is a power of two, it has solutions for other groups but even order groups give only multiples of two which can be factored out, so with this generator in use we only have to look at odd order groups. E.g. modulo seven there are solutions which repeat in cycles of 8. Since solutions can be added to give other solutions it is possible to combine with the solutions for the
is a power of two, it has solutions for other groups but even order groups give only multiples of two which can be factored out, so with this generator in use we only have to look at odd order groups. E.g. modulo seven there are solutions which repeat in cycles of 8. Since solutions can be added to give other solutions it is possible to combine with the solutions for the  sequences too giving mappings
sequences too giving mappings  .
.
This leaves the relation for …
…
Substituting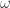 in the third line using the first line produces
in the third line using the first line produces  .
.
I should have double checked. Sorry, false claim.
to solve the equation recursively it needs to be transformed using
equation recursively it needs to be transformed using 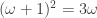

Use this to form a recurrence relation mod 5 for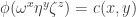 . For fixed
. For fixed 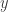 this has period 6 in
this has period 6 in  and is one of the sequences 1,2,1,4,3,4 or 3,1,3,2,4,2 up to cyclic permutations.
and is one of the sequences 1,2,1,4,3,4 or 3,1,3,2,4,2 up to cyclic permutations.
The inverse of 3 mod 5 is 2 (note that this step is problematical when working modulo a multiple of three) so the recurrence relation in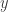 is
is
Now we can try all possible initial conditions for the recurrence relation to find all solutions that do not have any zeros. I find that there are four solutions up to cyclic permutations in or
or 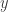 that repeat after eight steps. These four solutions are related by a non-zero factor mod 5, so I think there is really just one distinct solution tabulated as follows
that repeat after eight steps. These four solutions are related by a non-zero factor mod 5, so I think there is really just one distinct solution tabulated as follows
1 2 1 4 3 4
2 1 4 3 4 1
1 3 2 4 2 3
2 4 2 3 1 3
4 3 4 1 2 1
3 4 1 2 1 4
4 2 3 1 3 2
3 1 3 2 4 2
I am assuming there are not other independent polynomial relationships between ,
,  and
and 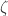 . Do we know that?
. Do we know that?
Apparently, the sort of graph we are studying (in which the vertices are members of a ring, and vertices share an edge when their difference is a unit in the ring) is called a unitary Cayley graph. For finite rings, these graphs seem to be well understood. When the ring is , Theorem 1 in [1] demonstrates that the chromatic number equals the clique number, which in turn equals the smallest prime divisor
, Theorem 1 in [1] demonstrates that the chromatic number equals the clique number, which in turn equals the smallest prime divisor 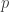 of
of 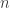 . This is proved by identifying
. This is proved by identifying  as a clique and identifying each coset of
as a clique and identifying each coset of  as an independent set (i.e., they serve as proper color classes). Theorem 2 in [2] demonstrates that these color classes are forced when coloring with
as an independent set (i.e., they serve as proper color classes). Theorem 2 in [2] demonstrates that these color classes are forced when coloring with 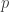 colors. Finally, [3] studies unitary Cayley graphs over arbitrary finite rings, and Proposition 6.1 in this paper is the appropriate generalization of Theorem 1 in [1]; in this general setting, we still have the chromatic number equaling the clique number, and presumably, the coloring is still unique.
colors. Finally, [3] studies unitary Cayley graphs over arbitrary finite rings, and Proposition 6.1 in this paper is the appropriate generalization of Theorem 1 in [1]; in this general setting, we still have the chromatic number equaling the clique number, and presumably, the coloring is still unique.
I noticed that the Moser spindle is generalizable to higher dimensions. Perhaps generalizing a 5-chromatic graph to higher dimensions would produce insight into why the graph works.
For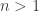 , a lower bound of
, a lower bound of  is available using a generalization of the Moser spindle: a pair of the objects(each 2 simplexes glued together on a face) which are joined on 1 side by a point and the other side by a line.
is available using a generalization of the Moser spindle: a pair of the objects(each 2 simplexes glued together on a face) which are joined on 1 side by a point and the other side by a line.
Improving the lower bound to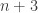 for
for 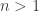 seems like an interesting side-quest anyway.
seems like an interesting side-quest anyway.
According to Soifer’s “The Mathematical Coloring Book,” the best known lower bounds in 3, 4, 5, and 6 dimensions are 6, 7, 9, and 11, and the chromatic number in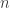 dimensions is at least
dimensions is at least 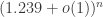 .
.
I found that [A.M. Raigorodskii, On the chromatic number of a space, Russian Math. Surveys, 55 (2000)] is behind a paywall, yet https://arxiv.org/abs/1512.03472 is accessible.
A few records have been broken in small dimensions since the publication of Soifer’s book. In particular chi(R^4) is at least 9.
https://link.springer.com/content/pdf/10.1007/s00454-014-9612-7.pdf and chi(R^6) is at least 12. https://arxiv.org/pdf/1408.2002.pdf
An observation: The record-holding graphs in all dimensions >= 4 are of a very different and simpler character than those in dimensions 2 and 3. They consist of simple transformations of the coordinates of a very small numbers of vertices. I suspect that the algebraic analysis being discussed here has the potential to lead to new lower bounds – posssibly breaking existing records by quite a lot – by starting with a larger number of generating vectors/vertices, derived from promising rings.
In order to determine whether this suspicion has legs, I suggest we look at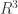 in a bit more detail. Last December I had a go at it and came up with a 6-chromatic construction that has a lot in common with Nechushtan’s 2002 one, but which is not only smaller, it’s also more regular and thus perhaps more usable as a building-block.
in a bit more detail. Last December I had a go at it and came up with a 6-chromatic construction that has a lot in common with Nechushtan’s 2002 one, but which is not only smaller, it’s also more regular and thus perhaps more usable as a building-block.
Its starting-point is a 20-vertex structure built from two copies of the 10-vertex “basic construction” that is shown in Nechushtan’s Figure 3. That figure is quite hard to interpret: it consists of two copies of the six-vertex polyhedron that arises from glueing faces of three tetrahedra together. The copies are joined at both their tips, i.e. the vertices labelled p and q in his figure, and then mutually rotated so as to introduce two additional edges that are labelled p1-p1 and p2-p2 in his figure.
The neat feature of this 5-chromatic, 10-vertex structure is that if p and q are constrained to be different colours, then one of the vertices that he labels p1 must be the same colour as q and one of his p2’s must be the same colour as p. This means that an eleventh vertex r can be added that is joined to (say) both the p1’s, and thus is necessarily coloured differently from q whenever p and q are different colours. Since it is only connected to two other vertices, the triangle p1-p1-r is a “flap” that is free to rotate around the p1-p1 line, and Nechushtan uses this property to arrive at his 6-chromatic thing.
My 20-vertex structure (which I’m calling a clamp) is then made by spindling two of the above 11-vertex things at their tips – coinciding the q’s and attaching the p’s – and then mutually rotating them so that their r’s coincide. In this structure, since one of the p’s must be differently coloured than q, r must be different from q in any 5-colouring – but the “double flap” with tip r is still rotatable, such that the distance qr can vary within a rather large range (between roughly 1 and 2.5).
We can therefore create a 6-chromatic graph by taking any six-vertex graph all of whose non-connected vertex pairs are a distance apart that lies within that range, and identifying the two vertices of each such pair with q and r of a copy of the clamp. An obvious such six-vertex graph is the unit-edge octahedron, which has three such vertex pairs all at distance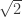 and thus gives rise to a 60-vertex 6-chromatic graph with lots of nice symmetry properties as well as the ability to rotate the clamps around mutually perpendicular axes.
and thus gives rise to a 60-vertex 6-chromatic graph with lots of nice symmetry properties as well as the ability to rotate the clamps around mutually perpendicular axes.
Unfortunately I have failed to exploit these properties to get to a 7-chromatic structure, but I feel sure it’s possible.
What about a hexagon with its centre. Your construction shows any six of the points must have different colours; so all seven must.
Sorry, I misunderstood. The clamps won’t work anymore if six colours are available.
Right, exactly. My expectation is that, as with the plane, levelling up to an additional colour will be really hard. But my hope is that the crafty group-theoretic tricks that are emerging in this thread will guide that process. For example: the moral equivalent in 3D of the Moser spindle is the 13-vertex structure in which three bi-tetrahedra share one tip and have their other tips in a triangle. We can extend that triangle into a lattice that covers the surface of a sphere (it doesn’t join up nicely, of course, but we can keep going anyway), and we can also add rotations of that lattice so as to coincide this or that set of vertices of different lattices. Then we add the fact that each individual bi-tetrahedron can rotate on its long axis, and it really seems like something should be possible.
Each of Marijn’s 826 and 874 vertex constructions, as well as Jannis’ 1951, 2653 and 3085 vertex graphs and my triple Minkowski sum critically depend on the following implicit unit distance (the red dashed line on the picture):
https://htamas.ces.hu/files/cnp/implunit/
Note that the red line is not a continuation of the blue one, it has a kind of arbitrary angle which is not in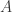 .
.
Furthermore, this is the only kind of special unit segment that appears in the constructions.
To make it more precise, I’m borrowing Dustin’s (slightly modified) notation of spindling angles and chord angles
and chord angles 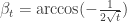 . Each of the edges in the aforementioned examples are the linear combination of some
. Each of the edges in the aforementioned examples are the linear combination of some  ‘s and
‘s and 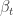 ‘s where
‘s where  together with the angle of the red edge on my figure. If we only keep those edges where we don’t use the angle of the red edge in the linear combination, all of the graphs become 4-colourable.
together with the angle of the red edge on my figure. If we only keep those edges where we don’t use the angle of the red edge in the linear combination, all of the graphs become 4-colourable.
Aubrey’s original 20425 vertex graph also contains these special unit segments but the dependence is no longer critical, i.e. the graph remains 5-chromatic even after removing them. Interestingly enough, this already happened in the reduced 1585 vertex construction
also contains these special unit segments but the dependence is no longer critical, i.e. the graph remains 5-chromatic even after removing them. Interestingly enough, this already happened in the reduced 1585 vertex construction 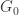 , all of whose edges have angles that are linear combinations of
, all of whose edges have angles that are linear combinations of  ‘s and
‘s and 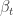 ‘s only. In exchange for the red edge, we have to allow
‘s only. In exchange for the red edge, we have to allow  here, corresponding to spindling with side length 4 in section 3.4 of the article.
here, corresponding to spindling with side length 4 in section 3.4 of the article.
Brilliant, you found it! Very interesting. I guess the next question is, can we add this angle to V and obtain any simplifications?
Historical note: I noticed these unplanned edges back in early February while I was in the early stages of shaving down the 20425er, and I also noticed that they disappeared during the reduction that I describe in Section 5.5, but I never explored their significance. Very interesting to see that they have some!
A small observation: The graph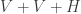 not only precludes monochromatic triples, but forces the point
not only precludes monochromatic triples, but forces the point  to have the same color as the origin. This allows for a simple spindle construction with the angle
to have the same color as the origin. This allows for a simple spindle construction with the angle  moving that point by a distance of 1. The smallest subgraph of
moving that point by a distance of 1. The smallest subgraph of 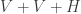 that I was able to find and still has the same property and symmetries has 745 vertices: https://files.jixco.de/pm16/745.vtx
that I was able to find and still has the same property and symmetries has 745 vertices: https://files.jixco.de/pm16/745.vtx
Wow! I REALLY should have spotted that. Everyone please note that this is my original V that Jannis refers to, as opposed to Tamas’s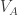 . Thus, we now have something 5-chromatic that does not have a spindling at distance 2, only at distances
. Thus, we now have something 5-chromatic that does not have a spindling at distance 2, only at distances 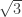 and 8/3. The following questions immediately arise:
and 8/3. The following questions immediately arise:
1) Can V+V+V be cut down to something smaller than 745 that still forces (8/3,0)? This is plausible because it would mirror my experience: when I was just forbidding mono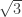 triangles I got to 667 vertices for my graph S by starting with V+V+H but when starting with V+V+V I got to 439. (The remaining 42 vertices that I removed in getting to the 397er in the paper were with the method described in section 5.5.)
triangles I got to 667 vertices for my graph S by starting with V+V+H but when starting with V+V+V I got to 439. (The remaining 42 vertices that I removed in getting to the 397er in the paper were with the method described in section 5.5.)
2) Let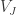 be the 60-edge star formed by spindling V at distance 8/3. Then clearly the Minkowski sum of three of it is 5-chromatic. Tamas spindled V at distance 2, also giving a 60-edge star, and was able to reduce that to 36 edges without allowing a 4-colouring of the three-fold sum. Can we reduce
be the 60-edge star formed by spindling V at distance 8/3. Then clearly the Minkowski sum of three of it is 5-chromatic. Tamas spindled V at distance 2, also giving a 60-edge star, and was able to reduce that to 36 edges without allowing a 4-colouring of the three-fold sum. Can we reduce 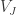 similarly, or further?
similarly, or further?
3) In Jannis’s graph I presume we force all of the six 60-degree rotations of (8/3,0) to be the same colour as the centre. How much more can we shave off if:
a) we only force (8/3,0) itself? The best graph will presumably have mirror symmetry about the x-axis but no rotational symmetry
b) we force at least four of the six, without specifying which ones?
c) we force at least one of each opposite pair?
d) we force both of at least one opposite pair?
We could then get 5-chromaticity by pairing two of (a), or two of (b), or one of (c) with one of (d). The last of these mimics my Sa and Sb in the paper.
Hmm. This means my virtual edge idea works; the set of points distance 1 from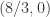 produces virtual edges of distances in the range
produces virtual edges of distances in the range  .
. exist.
exist.
Noting
What is the chromatic number of your graph? Say your graph has the chromatic number $\latex n$ The chromatic number of the plane is at least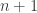 , as shown by considering an arbitrary set of $n$ points all with a distance of at least
, as shown by considering an arbitrary set of $n$ points all with a distance of at least  from every other point.
from every other point.
Corollary: No unit distance graph in with the same chromatic number as
with the same chromatic number as  can force 2 nodes to be the same colour.
can force 2 nodes to be the same colour.
What procedure did you use to find (8/3,0)? Can you run a similar procedure on one of the 5-chromatic graphs?
I used a SAT solver to compute an initial 4-coloring. This gives me a candidate set of vertices that received the same color as the origin. Using a constraint that forces at least one candidate to have a different color I repeatedly excluded candidate vertices until the problem became unsatisfiable. The candidates left are the set of forced vertices.
With a given 5-chromatic graph, I would need to guess a suitable 4-chromatic subgraph. I don’t have a method to automatically find such a subgraph. Given a minimal 5-chromatic graph it might be fast enough to check all subgraphs with one vertex removed which I will try later.
> I would need to guess a suitable 4-chromatic subgraph
I don’t understand. I’m wondering if any of our current 5-chromatic graphs have the property that for every proper 5-coloring, one of the vertices always receives the same color as the origin. It seems like your approach would identify such a vertex.
I misunderstood your question (I was too focused on what I was currently trying). Yes that does work, I’ll try it now.
It should be possible to use the homomorphic colourings to narrow down the points that must have the same colourings before resorting to the SAT solver. It may even be possible to do that for more colours on more complex graphs
I also observed that points which are 8/3 apart from each other are forced to the same color when coloring with only four colors. For several days I have tried to find a new record using this observation by 1) picking such a pair, 2) forcing them to have a different color, and 3) reduce the graph using random probing via clausal proof minimization. However, this approach has not been fruitful yet: the smallest graphs with chromatic number 5 based on this are roughly 150 vertices larger than the earlier method.
Forcing the points (0,0) and (8/3,0) to the same color can be done without any points that have a y coordinate larger than 1 or lower than -1. This is probably not tight. I will also try to minimize this.
Many thanks Marijn – very interesting. A variation that might also be worth a look is to use (-8/3,0) and (8/3,0) as the forced pair.
I tried forcing the pair (-8/3,0) and (8/3,0) and minimizing the graph, but the result was worse than forcing the pair (0,0) and (8/3,0). Also, the SAT problem to check whether (-8/3,0) and (8/3,0) must have the same color in every 4-coloring is noticeably harder than checking whether (0,0) and (8/3,0) must have the same color in every 4-coloring.
Note: apparently I did not proofread before posting: Use the multiplicative property of virtual edges using distances between .
. 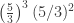 are valid virtual edges.
are valid virtual edges.
Something is wrong with my posts. They are not showing as I typed them. Without latex:
Use the multiplicative property of virtual edges using distances between 5/3, 11/3. This means all virtual edges larger than (5/3)^2 are valid.
Does anyone know a convenient way to preview latex WordPress comments?
Because the goal of this project is to simplify the proof of the lower bound rather than finding the smallest unit distance graph which is not 4 colourable, I suggest we switch to finding the smallest 4 colourable graph which forces 2 nodes to be the same colour, because as shown with the virtual edge argument, such a graph proves the chromatic number of the plane is at least 5.
The “virtual edge argument” is materialized by what most people here refer as “spindling”, i.e., rotating a set of vertices S about a vertex u in S, in a way that a vertex v in S and its image by the rotation are at distance 1. So indeed, we know that a set of s points which induces a 4-chromatic unit-distance graph where all 4-colorings give the same color to two distinct vertices immediately yields a set of at most 2s-1 points which are not 4-colorable.
Ah, yes. Ignoring virtual edges is simpler in this case.
There is a useful result if you are looking for complex numbers of unit norm in a field . They are always products of units of the form
. They are always products of units of the form  where
where 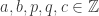 . There must be a standard reference to this but it can be proved by induction on
. There must be a standard reference to this but it can be proved by induction on  taking two extensions at a time.
taking two extensions at a time.
Sorry it would have been clearer to write that as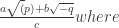 latex a,b,c,p,q \in \mathbb{Z}, p>0, q>0 $
latex a,b,c,p,q \in \mathbb{Z}, p>0, q>0 $
If only we could edit our own posts, one last try: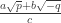 where
where 
My current plan is to preview every single post in TeXstudio. My plan is to always leave a space before every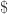 which begins a math mode yet never before a
which begins a math mode yet never before a 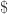 which ends a math mode. After achieving the post preview I want, Ctrl+R replace all `
which ends a math mode. After achieving the post preview I want, Ctrl+R replace all ` 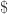 ‘ with `
‘ with `  latex ‘. During the second preview, I will see a `latex’ artifact at the beginning of every math typesetting, yet checking again is good. A problem with previewing this post is the fact that I needed to escape the
latex ‘. During the second preview, I will see a `latex’ artifact at the beginning of every math typesetting, yet checking again is good. A problem with previewing this post is the fact that I needed to escape the  characters. I used
characters. I used  , as every
, as every  needing escaping had a space before it. Another option which does not require the leading space is replacing
needing escaping had a space before it. Another option which does not require the leading space is replacing  ( and
( and  ) with
) with 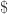 latex and
latex and 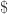 , respectively. If all goes as planned, this should look as desired when posted.
, respectively. If all goes as planned, this should look as desired when posted.
Well, the upside of inability to edit posts is that LaTeX newbies like me can see and memorise the codes for symbols! 🙂
Fyi, you can mouseover any of the math on this blog and it will display the LaTeX source. There is also a helpful tool online called “detexify” that may be useful.
@Boris: I’ve known about detexify for a while but I was blissfully unaware of the tooltip, that’s useful indeed, thanks for the heads up.
Here is a quick followup to the comment that Bernhard Hockertz posted yesterday on the first thread:
Bernhard: even though this project is focused on the lower bound in the plane, I think there is plenty of interest in higher dimensions and in the upper bound, so I encourage you to share what you have developed regarding exclusion zones. To my knowledge, much less work has been done in that area. The most significant work I know of involves analysis of the “permutohedron”:
https://en.wikipedia.org/wiki/Permutohedron
which tesselates for any n. By clever use of modular arithmetic Radoicic and Toth derived colourings of such tesselations in
for any n. By clever use of modular arithmetic Radoicic and Toth derived colourings of such tesselations in  and
and  that provide upper bounds of 15 and 54 colours respectively:
that provide upper bounds of 15 and 54 colours respectively:
http://www.cs.bme.hu/~geza/chromatic.pdf
I implemented their approach a few months ago and obtained provisional bounds of 156 and 564 for and
and 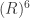 respectively. However, the natural way forward is to seek alternative tesselations, and I made no progress on that.
respectively. However, the natural way forward is to seek alternative tesselations, and I made no progress on that.
Then I shall do so, I’ve been looking into ways and places to share my work and I think this might be the best time and place given the spike of interest in this problem.
Small background information about me, I’m working mostly in the area of programming but always had a bit of fascination with math, occasionally attempting hard problems for fun, but usually I gave up pretty quickly. Around 8 months ago I ran into a video by PBS Infinite Series briefly mentioning this problem and I got caught by it, having worked on it in earnest ever since.
These 8 months include me studying up on various topics such as set and graph theory as well as topology. I’m not associated with an university and my previous schooling also contributed little to my math knowledge, so I’m a mostly self-taught amateur.
And indeed it was exactly the paper you linked I have worked with closest over time, and I have more conjectures along those lines, ultimately linking permutahedra to sphere packing, but these are in their very early infancy, and well, probably wrong, even if they work in R^2 and R^3. They shouldn’t be too hard to test and debunk but I’ve only started working with SAGE seriously a month ago.
I’ll write up a brief summary here of what I’ve been trying to do so far in my own paper. The notation might not be perfect but I did my best to put everything into already existing and well-defined terms. It uses LaTeX extensively and includes a couple illustrations to bring the points across better as well, so its 6 pages shouldn’t be painful too look at.
The exclusion zone function I defined is essentially the union of all hyperspheres centered around all vertices of the input set.
This has 3 uses to my knowledge. The first one is simplifying tesselations into locally finite (non unit distance) graphs with the same chromatic color by turning each single-colored tile into a node, and edges are between all nodes that touch each other with their exclusion zones.
The second use is finding out if the graph is connected to the entire space it is contained in or if it is a “tessellation” of its containing space by multiple disconnected graphs. R^1 and the example given on the De Bruijn–Erdős theorem wikipedia page are examples of disconnected graphs. I’m not aware of any solved chromatic problems that involve space filling connected graphs.
The third use is… take it with a bag of salt coming from an amateur, but I think it can point out contradictions in the use of anything less than n-manifolds to tesselate R^n, which would very well improve the lower bound not just in 3 dimensions and higher, but in 2 dimensions as well. Specifically if this is true then there should be a way to prove that a coloring of R^n doesn’t just rely on n-manifolds, but more specifically a lattice-sublattice scheme which would make 7 the definitive answer, but again, wild conjecture here. I simply haven’t had the time to chew through the according papers.
Bold claims, but I haven’t been able to debunk them myself for a solid month, so I guess some more professional people than me with my 6 months are needed to confirm or debunk this.
There are some minor issues in the paper I’m aware of but here it is:
https://www.dropbox.com/s/elsmbzogdn2r7g2/Note%20on%20exclusion%20zones%20in%20graph%20theory%20and%20the%20chromatic%20number%20of%20euclidean%20spaces.pdf?dl=0
Looking forward to seeing my work debunked/confirmed, and I hope it turns out to be useful. And if my stuff turns out to be true to even some degree, than this would raise the question where exactly the link is to finite unit distance graphs and their chromatic number. There would have to be such a connection but I don’t even have an idea of where it would be, that’d be much closer to the other work done in this polymath project.
By improving the heuristics, the random probing approach found an even smaller unit-distance graph with chromatic number 5. This one has 803 vertices and 4144 edges. The graph is available here:
* http://www.cs.utexas.edu/~marijn/CNP/803.vtx
* http://www.cs.utexas.edu/~marijn/CNP/803.edge
Visualizations based on a 5-coloring of this graph are here:
* http://www.cs.utexas.edu/~marijn/CNP/803.pdf
* http://www.cs.utexas.edu/~marijn/CNP/803black.png
Similar files of the prior records (the ones with 826 and 874 vertices) are stored at that location as well: Simply replace 803 in the links above to either 826 or 874 to access them.
I have been trying to catalogue examples of small unit distance graphs with chromatic number 4. For instance:
– We know the Moser spindle is minimal, in the sense that unit distance graphs on fewer than 7 vertices are all 3-colorable.
– I’ve verified that the Moser spindle is the only 7-vertex 4-chromatic unit distance graph, and that every 8-vertex 4-chromatic unit distance graph contains the Moser spindle as a subgraph.
– Two examples of a 9-vertex 4-chromatic unit distance graph are given by (1) deleting an “outer” vertex of degree 3 from the Golomb graph, or (2) rotating a 4-vertex diamond out of a 7-vertex hex. There are most two other examples that do not contain the Moser spindle as a subgraph; I am still considering whether they are unit distance or not.
– Here is an interesting unit distance graph on 10 vertices with chromatic number 4 that is flexible (i.e. it admits a continuum of embeddings):
Dustin tells me that Boris found this graph online here:
http://mathforum.org/kb/message.jspa?messageID=9346194
and it was animated with Geogebra. Notice that it degenerates into smaller 4-chromatic examples when the vertices overlap.
Nice! A simpler case (well, conceptually simpler – same numbers of vertices and edges) is a cycle consisting of three diamonds and an edge, i.e. a Moser spindle expanded by an extra diamond. The existence of these examples certainly supports the idea that flexible graphs should be good building-blocks for a higher chromatic number, but Paul O’Donnell’s extensive efforts along those lines 20 years ago were unsuccessful. It would certainly be terrific if we could gain some insight as to why.
This is a continuation of the discussion of Jannis’s method for identifying vertices that must be the same colour in any 4-colouring. Dustin’s suggestion to use the same idea to get to a 6-chromatic graph can be generalised in at least a couple of ways, so I think it will help if I write this as a separate post rather than as a reply, given that quite a few other posts are already more recent.
First there is the class of generalisations that I mentioned to Jannis two days ago (see above, April 28th 2:38pm) in the context of shrinking his graph. I’m thinking it should be possible to use SAT to look for similar things: a set of vertices that lie on a circle and more than half of which are always the same colour as the centre of the circle, for example.
Then there is the class of “virtual edge” approaches, i.e. cases where two specific (non-connected!) vertices are never the same colour in any k-colouring. I mentioned recently that for k=4 there are two particularly useful distances that we’d like to see between such vertices, namely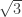 and phi, since there are unit-distance graphs (a pair of half-hexagons spindled at distance 2 and a regular pentagon, respectively) that can be rendered 5-chromatic by clamping 4 or 5 (respectively) pairs of vertices with copies of such a graph. I failed to find other examples but I didn’t try very hard. The holy grail here would be a flexible example, analogous to the 3-dimensional 5-chromatic case I described recently. As such, there may be mileage in seeking flexible 5-chromatic graphs.
and phi, since there are unit-distance graphs (a pair of half-hexagons spindled at distance 2 and a regular pentagon, respectively) that can be rendered 5-chromatic by clamping 4 or 5 (respectively) pairs of vertices with copies of such a graph. I failed to find other examples but I didn’t try very hard. The holy grail here would be a flexible example, analogous to the 3-dimensional 5-chromatic case I described recently. As such, there may be mileage in seeking flexible 5-chromatic graphs.
Clearly there are lots of extensions and combinations of these approaches, though it’s less clear (to me) where that rabbit-hole would become SAT-unfriendly.
I just found two other lengths of a 4-chromatic virtual edge that let us build something 5-chromatic: . Let ABC be a unit triangle and let the unit edges AD and BE bisect BAC and ABC respectively, either both internally or both externally. Then the lengths AE, BD, CD and CE are all equal (with the lengths just given) and we can spindle using DE.
. Let ABC be a unit triangle and let the unit edges AD and BE bisect BAC and ABC respectively, either both internally or both externally. Then the lengths AE, BD, CD and CE are all equal (with the lengths just given) and we can spindle using DE.
[Fixed. – M.]
If a virtual edge length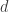 is found, then length
is found, then length  may also be used because this problem is scale invariant. The same minimum number of colors will be used whether the circles have radius
may also be used because this problem is scale invariant. The same minimum number of colors will be used whether the circles have radius 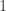 or radius
or radius 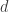 , so we could pretend
, so we could pretend 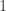 is
is  and
and 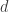 is
is 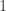 for convenience’s sake.
for convenience’s sake.
If 2 different virtual edges,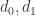 are found such that
are found such that 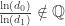 , then combined with scale invariance, a set of virtual edge lengths which densely covers
, then combined with scale invariance, a set of virtual edge lengths which densely covers 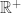 is produced. Such dense covering would likely be helpful somehow.
is produced. Such dense covering would likely be helpful somehow.
I don’t follow your scale invariance claim. A coloring of the plane for unit distances is not necessarily a coloring of the plane for some other distance. Case in point, the 7-coloring using a hexagon tiling is not a coloring for the distance 0.1 because nearby points receive the same color.
Not sure I understand and follow this claim either. Sounds to me like you’re saying that if we find not just any type of virtual edge, but two that have a non rational ratio we can go from there and create virtual edges of arbitrary length.
At the very least finding virtual edges of truly arbitrary length can’t be possible, as the implication is an infinite chromatic number, since we could create arbitrary complete subgraphs.
Assuming I got all of that right I’d be pretty sure that virtual edge lengths are going to be tightly related to the unit distance, such as only being rational.
Yeah I think Nazgand’s statement about scale-invariance combines the two required components in a slightly unclear way. What was meant is that if a graph G is found that could be rendered 5-chromatic by being combined with (some number of copies of) a graph H that has a virtual edge of length d, then G (as opposed to H) can be scaled so that 1 and d become 1/d and 1 respectively, meaning that the same graph G could alternatively be rendered 5-chromatic by instead being combined with copies of a graph H’ that has a virtual edge 1/d.
@ag24ag24: That makes a lot more sense to me than his initial post, thanks for the clarification.
To be more clear: can be created, though I would not be surprised. To be more clear:
can be created, though I would not be surprised. To be more clear:
I am no claiming that a graph which virtualizes the edge
Consider the problem : coloring of the plane which satisfies the condition that points distance
: coloring of the plane which satisfies the condition that points distance  apart do not have the same color. The chromatic number of the place, CNP, is the minimum number of colors required for a solution to
apart do not have the same color. The chromatic number of the place, CNP, is the minimum number of colors required for a solution to 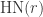 for any
for any  because Euclidean geometry is scale-invariant. Any solution of
because Euclidean geometry is scale-invariant. Any solution of 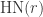 can be scaled to produce a solution of
can be scaled to produce a solution of 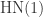 .
.
Suppose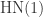 has a virtual edge length
has a virtual edge length 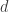 produced by graph H of chromatic number
produced by graph H of chromatic number  . Then scaling the graph H produces a virtual edge if the different problem
. Then scaling the graph H produces a virtual edge if the different problem 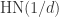 with length 1 and chromatic number
with length 1 and chromatic number  . If virtual edge length
. If virtual edge length 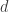 has the chromatic number CNP, then
has the chromatic number CNP, then  .
.
What I am proposing, adding a virtual edge length , is equivalent to moving to the different problem
, is equivalent to moving to the different problem 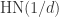 . This move may cause some valid solutions of
. This move may cause some valid solutions of 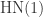 to no longer be valid, yet will not increase the required colors while supplying more intuitive methods of finding CNP. The multiplicative property of virtual edges still hold by moving from
to no longer be valid, yet will not increase the required colors while supplying more intuitive methods of finding CNP. The multiplicative property of virtual edges still hold by moving from  to
to  when multiplying
when multiplying  different virtual edges together. Which specific problem we are working in does not have any significance.
different virtual edges together. Which specific problem we are working in does not have any significance.
> there may be mileage in seeking flexible 5-chromatic graphs
Recall that Jannis’s observation [1] gives that any 4-coloring of M forces (0,0) and (8/3,0) to receive the same color. With this, we can generalize your point in [2] to build non-rigid 5-chromatic graphs. In particular, take a cycle consisting of a several edges of length 8/3 and a single edge e of length 1. Observe that this cycle is not rigid. Now replace each edge of length 8/3 with a copy of M, placing the vertices from (0,0) and (8/3,0) at the endpoints. Then this graph is both non-rigid and 5-chromatic, since any 4-coloring of this graph forces the endpoints of e to have the same color.
Ah yes, of course – analogous to the 10-vertex 4-chromatic graph I described yesterday.
I checked whether 5-coloring Tamás’s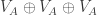 forces a vertex to have the same color as the origin, which it doesn’t. This seems to be around the largest 5-chromatic graph that finishes in reasonable time with my current approach.
forces a vertex to have the same color as the origin, which it doesn’t. This seems to be around the largest 5-chromatic graph that finishes in reasonable time with my current approach.
Instead of , we can try for
, we can try for 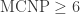 (see [1]). Consider all 5-colorings in which the neighborhood of the origin avoids colors 1 and 2. Is there any vertex (other than the origin) that is colored either 1 or 2 in all such colorings?
(see [1]). Consider all 5-colorings in which the neighborhood of the origin avoids colors 1 and 2. Is there any vertex (other than the origin) that is colored either 1 or 2 in all such colorings?
Here is a strategy that might work. Start with a set of unit vectors such as which are known to generate a 5-chromatic graph. Figure out the description of all the elements in the ring generated by these vectors, with both additions and multiplications. Find the element of the ring which is 5 times another element of the ring, and which is the sum of the smallest number of the unit vectors. For example if there is such an element which is the sum of four elements in
which are known to generate a 5-chromatic graph. Figure out the description of all the elements in the ring generated by these vectors, with both additions and multiplications. Find the element of the ring which is 5 times another element of the ring, and which is the sum of the smallest number of the unit vectors. For example if there is such an element which is the sum of four elements in  then it would be in the graph
then it would be in the graph  If we are lucky it would be constrained to be the same colour as the origin in any 5-colouring. If not, we might achieve that with more vectors or more copies. The problem is that this might go beyond what a SAT solver can cope with in order to check it.
If we are lucky it would be constrained to be the same colour as the origin in any 5-colouring. If not, we might achieve that with more vectors or more copies. The problem is that this might go beyond what a SAT solver can cope with in order to check it.
I want to revisit the ring generated by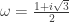 and
and  . The motivation is that this is the smallest ring that contains a moser spindal. It’s elements of unit norm are generated as products of powers of
. The motivation is that this is the smallest ring that contains a moser spindal. It’s elements of unit norm are generated as products of powers of  and
and  .
.
A full description of the elements of this ring is the complex numbers of the form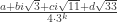 where
where 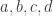 are all integers which are either all odd or all even and such that
are all integers which are either all odd or all even and such that 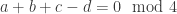 .
.  is a non-negative integer.
is a non-negative integer.
What 4-colourings are there that are homomorphisms to ? Zero will always map to zero and any number which is four times another element of the ring must also map to zero. The fraction
? Zero will always map to zero and any number which is four times another element of the ring must also map to zero. The fraction 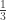 is in the ring so
is in the ring so  should map to zero, i.e. the same colour as the origin. This is stronger than what is observed for general 4 colourings where only
should map to zero, i.e. the same colour as the origin. This is stronger than what is observed for general 4 colourings where only  maps to the same colour as the origin. Unless I have made some error this means that there are 4-colourings which are not homomorphisms so it would be good to understand these algebraically if possible.
maps to the same colour as the origin. Unless I have made some error this means that there are 4-colourings which are not homomorphisms so it would be good to understand these algebraically if possible.
An example of a homomorphic colouring that works is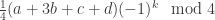
I think the ring is smaller than that, I think it is just
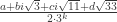
 is even. For example, your ring contains
is even. For example, your ring contains  , and I don’t think that is in the ring generated by
, and I don’t think that is in the ring generated by  and
and  . That doesn’t change your observation about
. That doesn’t change your observation about  though, so I’ll think about that.
though, so I’ll think about that.
where
I could be wrong, but if we multiply and
and  does not that give something with four odd coefficients over 12?
does not that give something with four odd coefficients over 12?
Sorry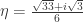
It is possible that if the graph was enlarged to include more of the ring then 4/3 would also be forced to take the same colour as the origin. I think the reason 8/3 comes out is because it is a sum of fewer generating elements. This would be consistent with the hypothesis that all 4-colourings of the ring are homomorphic colourings.
Does anyone know what the lowest diameter 5-chromatic unit distance graph is we currently know of, regardless of vertice count?
I don’t know what the lowest is, but Tamás’s construction [1] has diameter 6.
6? That seems huge compared to what I would expect to be the lowest possible. I manually measured the 803 vertex graph mentioned in this post: https://dustingmixon.wordpress.com/2018/04/22/polymath16-second-thread-what-does-it-take-to-be-5-chromatic/#comment-4105
But it still is 5, and I would expect the smallest 5-chromatic example to be much smaller. Thanks for the heads up, I guess the others will be in this ballpark so I’ll work with that for now.
I think Dustin was using the graph-theoretic definition of “diameter”, which is the largest number D for which there are two vertices between which one cannot travel along edges without using at least D edges, whereas you seem to be using the Euclidean definition.
Right, I missed that. But to make it clear, you’re correct, I do mean the euclidean definition, that is I’m curious about the euclidean distance between the two vertices of a 5-chromatic graph that are the furthest away. I’ve made this a bit clearer in the new, third thread.
Tamás’s construction also has Euclidean diameter 6.
The current record may actually be my original 1581er, with a Euclidean diameter just under 4.5.
So 6, 5 and 4.5 then. I just realized a couple other things about the connection from manifolds to finite unit distance graphs, but I’ll post that over in the third thread once I’m done.
Everyone: please note that Dustin just rolled over to a new thread (I know not everyone noticed last time so I thought it was worth this post).