Equiangular tight frames (ETFs) are of particular interest throughout frame theory, and they are used in various sparse signal processing applications such as compressed sensing. The following paper describes how to build what are called harmonic ETFs:
Achieving the Welch bound with difference sets
Pengfei Xia, Shengli Zhou, Georgios B. Giannakis
Let denote the
discrete Fourier transform (DFT) matrix, and build
by collecting
rows of
and normalizing the columns. Such frames are called harmonic frames, and it’s easy to verify that
is an
unit norm tight frame. We are particularly interested in the inner products between columns of
. Specifically, we want to minimize the size of the largest such inner product, called the worst-case coherence. Recall the Welch bound: the worst-case coherence is
, with equality precisely when
is an equiangular tight frame (ETF), meaning every pair of distinct frame elements has the same sized (small) inner product.
The main result of this paper characterizes which choices of rows from make
an ETF:
Theorem (Xia, Zhou, Giannakis). Build by collecting rows from the DFT which are indexed by
. Then
is an ETF if and only if
is a difference set for
, that is, there exists a positive integer
such that every nonzero member of
can be expressed as the difference of members of
in exactly
different ways.
[UPDATE: Apparently, the “if” direction of the above theorem was first suggested by Strohmer and Heath using the Singer difference set and analysis from Konig.]
This characterization is particularly useful, considering difference sets are well-studied as combinatorial designs; this makes the construction of (harmonic) ETFs particularly easy, and this is precisely the message of the paper. After proving the above theorem, the paper provides a laundry list of difference sets, but I would instead consult this book for more information on difference sets (or any other sort of combinatorial design, for that matter). The remainder of the paper is, in my opinion, less exciting; the authors propose a numerical routine to find frames of small coherence, and they give an improvement to the Welch bound for the case where the number of vectors is larger than the square of the dimension.
The heart of the paper is identifying difference sets as the way to choose rows of a DFT to build harmonic ETFs. To make this clear, this blog entry will show why such a choice works (thereby proving the “if” direction of the above theorem). First, let’s understand how the Gram matrix of a harmonic frame
is related to the choice of rows. To this end, note that the
th entry of
is the inner product
.
Note that we take to be the DFT defined by
, so we don’t have a
factor floating around. The above equation shows that
is circulant, meaning all of the rows are translated versions of each other. Furthermore, the zeroth row of
is a multiple of the Fourier transform of (the indicator function of)
. Thus, minimizing the coherence of a harmonic frame corresponds to minimizing the largest nonzero Fourier coefficient of an indicator function.
Now that we’ve identified the Gram matrix with the Fourier transform of , let’s check that
is an ETF when
is a difference set. Considering the previous discussion, it suffices to study the nonzero Fourier coefficients of
:
.
Since is a difference set, we know every nonzero member of
can be expressed as a difference in exactly
different ways:
,
where the last step uses the fact that . The nonzero Fourier coefficients correspond to off-diagonal Gram matrix entries, and so
is equiangular since these entries all have equal size. Actually, we can make this more evident by demonstrating Welch-bound equality. Since every nonzero member of
must be a difference in exactly
different ways, and since there are
total differences available, we have
. Thus,
,
as desired.
Taking a step back, this characterization of harmonic ETFs leads to a particularly interesting idea for compressed sensing. By now, it is well known that selecting rows at random from a DFT will, with high probability, form a sensing matrix which satisfies the restricted isometry property (RIP). Here’s what’s interesting: A semi-recent development in additive combinatorics is the notion of Fourier-pseudorandomness. Specifically, is considered to be Fourier-pseudorandom if the largest nonzero Fourier coefficient of
is small. Since random subsets are Fourier-pseudorandom with high probability, this definition is reasonable. It’s also useful, as it guarantees certain desirable properties, such as random-like intersections. The reader is invited to google “Fourier-pseudorandom” for more information. All I care to mention is the following: Random sets correspond to RIP harmonic frames in the same way that Fourier-pseudorandom sets correspond to incoherent harmonic frames. But perhaps Fourier-pseudorandomness guarantees something much stronger. Certainly, low coherence doesn’t imply random-like RIP, but it might when you restrict to harmonic frames. This would be a monumental result for deterministic compressed sensing, and as this paper illustrates, it would have important consequences in number theory.
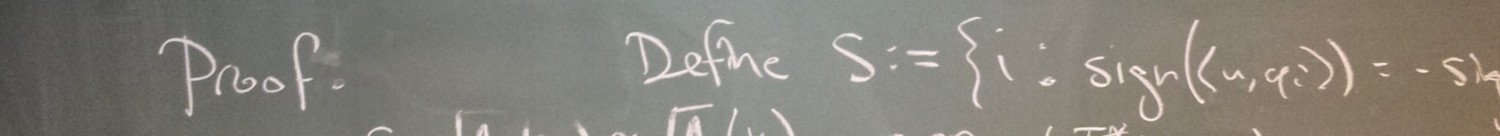
Dustin,
Do you think this approach by Meyer could be relevant ?
Click to access xong.pdf
Cheers,
Igor.
It’s certainly relevant. Two things comes to mind. First, Meyer’s paper is explicitly motivated by the fact that harmonic frames with a prime number of columns map sparse vectors injectively. This is an immediate consequence of a theorem by Chebotarev, as I discuss and generalize here:
Second, Meyer’s approach is quite different, since it deals with continuous functions as opposed to finite-dimensional vectors. The results are presented in the context of sampling and interpolation, which are introduced rather nicely here:
It’s striking that Meyer gets L1-minimization guarantees from mere injectivity. (Is the reconstruction stable if the measurements are corrupted with noise?) The guarantee requires the sparse function to be nonnegative, but is there an analogous result with finite-dimensional harmonic frames?
If you are asking me, I am not aware of any.