This is the fifth “research” thread of the Polymath16 project to make progress on the Hadwiger–Nelson problem, continuing this post. This project is a follow-up to Aubrey de Grey’s breakthrough result that the chromatic number of the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki page.
What follows is a brief summary of the progress made in the previous thread:
– We now have a 5-chromatic unit-distance graph with 633 vertices and 3166 edges. This is the current record holder.
– We now have a human-verifiable proof that there exists a finite unit-distance graph with a vertex
such that there is no 5-coloring of
in which
is bichromatic (see this and that). This result is “in between”
and
, since the latter implies the result, which in turn implies the former. Domotor suggests that this might be used to prove
.
– We’ve collected several probabilistic inequalities, but we’re still hunting for a human-verifiable contradiction. We have a short computer proof of , and we suspect there’s a human-verifiable proof within reach. Presumably, the proof will involve new ideas that can be leveraged for additional inequalities.
– is 5-chromatic, but so is
(see this). Details are being collected in the wiki. In order to build up to a 6-chromatic ring, we might need to analyze Jannis Harder’s ring
.
– Tamás Hubai identified all 4-colorings of with the help of a computer. These (finitely many!) colorings are invariant under translation by 8 and rotation by
. Presumably, this will help us identify useful claims about the colorings of
that are provable by hand.

This is a reply to Aubrey’s question on where my 43 vertex graph comes from. I took the Minkowski sum of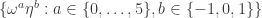 with itself and removed each circle (starting from the outside) whose removal still kept the graph non-4-colourable with a bichromatic origin.
with itself and removed each circle (starting from the outside) whose removal still kept the graph non-4-colourable with a bichromatic origin.
A possible next step would be to find a graph that has a specific copy of that cannot be colored with Aubrey’s upper left coloring (i.e. the outer ring cannot be bichromatic for just that one hexagon). Your 43 vertex graph might be a good place to start.
that cannot be colored with Aubrey’s upper left coloring (i.e. the outer ring cannot be bichromatic for just that one hexagon). Your 43 vertex graph might be a good place to start.
This is a bit of a big graph and thus probably not that interesting, but it might be a start assuming I did everything correctly:
Let S be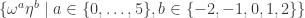 . Then take the three-fold Minkowski sum of S with itself (
. Then take the three-fold Minkowski sum of S with itself ( ), remove all of the points at unit distance from the origin except for the standard hexagon
), remove all of the points at unit distance from the origin except for the standard hexagon  , and call that graph
, and call that graph  . I think that
. I think that  cannot be properly 4-colored with a bichromatic origin, or equivalently
cannot be properly 4-colored with a bichromatic origin, or equivalently  cannot be properly 4-colored with a “2tri” hexagon (the top-left from Aubrey’s paper) at the origin.
cannot be properly 4-colored with a “2tri” hexagon (the top-left from Aubrey’s paper) at the origin.
I find that has 3427 vertices, so it’s a bit larger than Aubrey’s original graph, even though it only serves the role of
has 3427 vertices, so it’s a bit larger than Aubrey’s original graph, even though it only serves the role of  for a seven-vertex coloring.
for a seven-vertex coloring.
Woah, nice idea Boris!
First of all, actually something that only prohibits 2tri does not serve as M, since M must prohibit both 2tri and 1tri. But can you try this kind of idea with the variation that you also remove one vertex of the hexagon? If that works, it would prohibit both 2tri and 1tri (by sixfold rotation).
Second: if that’s possible, we can look at all our arsenal of shrinking techniques. Since in this context the main goal is to get to a human-comprehensible proof, my suggestion is to add unit-radius vertices back, one at a time, and find ones that allow large amounts of shrinking of S. That could be an efficient way to identify the “stepping-stones” that I mentioned in my post yesterday.
Specifically, in order to serve as stepping-stones, the vertices to add back should be ones that are present in one or other of the two human-comprehensible 26-vertex graphs that we currently have at our disposal. There are orientation ambiguities in that, of course, but in particular one should not add back vertices that complete a hexagon.
Thanks Tamas. Since you got it down to only four circles, it seems like it would not be combinatorially prohibitive to seek something even simpler by just checking all triples of circles irrespective of whether there are other smaller circles. It might also be worth trying the sum of my V with itself as the starting point; we’d probably end up with more vertices, but then it should be reasonably simple to identify dispensable ones manually in the same kind of way that I reduced your 43 to 34.
I wrote up Pace’s human proof of non-bichromaticity of the origin using Tamas’s graph in terms of the unit vectors at http://michaelnielsen.org/polymath1/index.php?title=Excluding_bichromatic_vertices , emphasising the 12-fold symmetry coming from rotations by
unit vectors at http://michaelnielsen.org/polymath1/index.php?title=Excluding_bichromatic_vertices , emphasising the 12-fold symmetry coming from rotations by 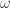 and complex conjugations. Everything takes place in (a finite subset of) the group
and complex conjugations. Everything takes place in (a finite subset of) the group  .
.
I think you mean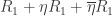 . Thanks for writing this up. Now I have a chance to understand it.
. Thanks for writing this up. Now I have a chance to understand it.
I have a small question for those who undersand Falconer’s proof of better than I do. Is there any prospect of identifying a condition that implies this but is weaker than the bichromaticity of the origin? For example, could it follow from a graph containing a set of at least two vertices not all of which can be simultaneously bichromatic? I’m thinking that the weaker we can go in this kind of direction, the more hope there is for finding a (large) graph that proves
better than I do. Is there any prospect of identifying a condition that implies this but is weaker than the bichromaticity of the origin? For example, could it follow from a graph containing a set of at least two vertices not all of which can be simultaneously bichromatic? I’m thinking that the weaker we can go in this kind of direction, the more hope there is for finding a (large) graph that proves  , given that Marijn reports getting close with the current criterion.
, given that Marijn reports getting close with the current criterion.
I think that there is a chance, but it won’t be so simple. The insight behind Falconer’s proof is that there is a point x on the boundary of two “differently colored” parts and a rotation of the rest of the graph so that every other vertex is not on a boundary. Then a small perturbation results in only x changing its color. Now, imagine that our graph is a triangular lattice and the coloring is given by parallel strips of width 1. Then this won’t be possible – if two vertices are on the boundary, there will be many others. Of course, this coloring is not proper (it has monochromatic unit distances in each strip), so using that the coloring is proper might help. I think I would first try to prove that there is an x on the boundary of three “differently colored” parts, which would give a trichromatic vertex. And maybe after this we can even rotate the graph around this x to find another vertex y that falls on two boundaries. So I think a possibly best result would be to prove that for any one vertex of the graph we can suppose that it’s trichromatic and for any other that it’s bichromatic. (And if there is, delete the edge among them.)
I don’t think it follows immediately, but such a result could conceivably be helpful. Roughly speaking, in the measurable case there are two types of points: “points of density”, which one can think of as being like “interior points” to one of the color classes, and “non-points of density”, which are like “boundary points”. If one has a configuration with one the points a non-point of density and all the others points of density, then one can jiggle the configuration a bit and arrive at the situation with one bichromatic vertex. If instead we can exhibit graphs with an edge of distance d in which both vertices cannot be simultaneously bichromatic, this means (roughly speaking) that the non-points of density avoid distances of length d. This by itself does not lead to a contradiction, but one could imagine that if one had several results of this type one could somehow use them to proceed further.
Thanks. OK – how about a different type of weakening? I am struggling to understand precisely what role sqrt(3) plays in Falconer’s logic. (OK, I admit it, I am also struggling even to understand how a set can be measurable without being “map-based” in the sense discussed by Woodall etc. If someone would enlighten me with an example I would be most grateful.) Can any distance whose arcsin is not a rational multiple of pi substitute for sqrt(3)? Can we adapt Falconer’s approach to make use of our discovery of graphs whose 4-colourings always have monochromatic vertex pairs at distance 8/3 ?
Non-map based measurbale sets, are we still talking about measures like the Lebesgues measure then? If you don’t mind could you point to the paper/article that discusses this issue?
I’m probably wrong but this faintly remembers me of a type of ordinal measure I briefly worked on which even seemed to work out so far, though I dropped that line of thought eventually in favor of other pursuits.
I generated and visualized about 100 graphs with 24 vertices for which no 4-coloring exists with a bichromatic origin. Not one of them is completely symmetric. In many of these graphs the origin connects two Moser spindles. This is clear in the image below.
Marijn, do you hae any completely symmetrical 25-vertex cases?
The smallest completely symmetric one I found has 26 vertices. See below.
Aha, and also it has only four distinct radii – nice!
This 26 vertex graph also has a short human proof. Notice how nicely all the vertices lie on the union of 3 unit circles. Since there are no numbers, I refer to the vertices of the innermost triangle as tri-top, tri-left, tri-right, and to the vertices at distance 1 from the origin as units. I suppose that the origin is colored 2 and 4. For other vertices, we only check whether they are colored with an odd (1 or 3) or with an even (2 or 4) color.
Case I: Tri-top is odd
1, Tri-left is even because tri-top and tri-left are in a pentagon with 3 units.
2, Tri-right is also even by symmetry.
3, The two lowermost vertices are even because they are each on a nonagon with tri-left and 7 units.
4, The lower leftmost vertex is odd because it form a triangle with tri-left and lowermost left.
5, The lower rightmost is also odd by symmetry.
6, Contradiction because the lower leftmost and lower rightmost from a heptagon with the origin and 4 units.
Case II: Tri-top is even
WLOG suppose that tri-left is even and tri-right is odd, because:
1, Tri-left and tri-right are not both odd, because they form a pentagon with 3 units.
2, Lowermost left is even, because it forms a heptagon with tri-right and 5 units.
3, Lower leftmost is odd because it forms a triangle with tri-left and lowermost left.
4, Upper leftmost is even, because it forms a nonagon with tri-right and 7 units.
5, This vertex for which I really don’t have a right name, but is between lower leftmost and lowermost is odd, because it form a triangle with upper leftmost and tri-left.
6, Contradiction, because this last vertex, lower leftmost, tri-right and 8 units from a hendecagon.
I found a way to reduce Tamas’s graph comprehensibly by four more vertices, i.e. to 30 (see below, presuming I get the dropbox link right this time, with vertices numbered).
Let the origin be either colour 2 or 4, so that the outer ring is all odd. If 13 and 19 are different then all three of 6, 10 and 18 are even, contradiction. So wlog let 13 and 19 be coloured 1, which makes 7, 11, 29 and 30 also 1; 3, 14, 16, 22, 25 and 27 all 3; and all of 4, 8, 12, 20, 23 and 26 even. Vertices 6, 10 and 18 can’t be all odd or all even. Also they can’t be two odd and one even: suppose wlog (which it will be because I’m not going to look at 2, 9, 17, 21, 5, 15, 24 or 28 yet) that 10 is even and 6 and 18 are odd, then the trapezium with vertices 6, 11, 18 and 30 will have three of one colour. So now let 10 be coloured 3, and 6 and 18 coloured 2 and 4 respectively. Then 4 and 12 are coloured 2 and 20 and 23 are coloured 4. But then 15 and 24 are both odd, and since they are connected to 11 and 30 they must be both 3. Oops, but they are also connected to 2 and 17, which are both odd but different colours. If instead 6 is the one coloured 3, and wlog 10 is coloured 2 and 18 is coloured 4, then 24 and 28 are coloured 3 – oops, but they are joined to 17 and 21 which are odd and connected. THe final case proceeds identically by reflection in the y-axis.
Ah – actually I am pretty sure that all parts of the above argument still work if we omit vertices 3, 12, 23 and 27. Yay, 26 and comprehensible!
I’ve put a new picture “nobio26.png” in the dropbox – let’s see if this works:
The numbering has changed, of course, so here is a revised proof. Let the origin be colours 2 and 4, so that the outer ring is all odd, alternating between 1 and 3 for 6, 22, 17, 20, 10 and for 25, 14, 11, 12, 26 and for 2, 8, 19, 15. If 11 and 17 are different then all three of 5, 9 and 16 are even, contradiction. So wlog let 11 and 17 be coloured 1, which makes 6, 10, 25 and 26 also 1; 12, 14, 20 and 22 all 3; and 3, 7, 18 and 23 all even. Vertices 5, 9 and 16 can’t be all odd or all even. Also they can’t be two odd and one even: suppose wlog (which it will be because I’m not going to look at 4, 13, 21, 24, 2, 8, 15 or 19 yet) that 9 is even and 5 and 16 are odd, then the trapezium with vertices 5, 10, 16 and 26 will have three of one colour. So now let 9 be coloured 3, and 5 and 16 coloured 2 and 4 respectively. Then 3 is coloured 2 and 16 is coloured 4. But then 13 and 21 are both odd, and since they are connected to 10 and 26 they must be both 3. Oops, but they are also connected to 2 and 15, which are both odd but different colours. If instead 5 is the one coloured 3, and wlog 9 is coloured 2 and 16 is coloured 4, then 21 and 24 are coloured 3 – oops, but they are joined to 15 and 19 which are odd and connected. THe final case proceeds identically by reflection in the y-axis.
[You can see the url of the figure by clicking on it. That is what the url will look like when done correctly. – M.]
Thanks Dustin. That’s what I tried first, though, and I always get URLs with “preview” in them. Maybe it’s because I’m not the owner? Bah.
@Aubrey – I think I know what’s going on. I have Dropbox installed on my computer. That means I can access the Polymath16 folder from Finder. This is where I “Copy Dropbox Link”:
I can’t figure out how to grab this url from the Dropbox website. The easiest solution might be to install Dropbox yourself:
https://www.dropbox.com/install
Very cool – will do – thanks again!
Aubrey’s original paper has a computer-verified proof that having a monochromatic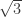 -triangle leads to a contradiction. Tamas’s original graph that excludes bichromatic vertices also gives a human-verified proof that having three bichromatic hexagons (at the vertices
-triangle leads to a contradiction. Tamas’s original graph that excludes bichromatic vertices also gives a human-verified proof that having three bichromatic hexagons (at the vertices 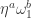 for
for  ,
,  ) leads to a contradiction. The smaller graphs obtained more recently should be able to replace the three bichromatic hexagon pattern by a smaller pattern and still obtain a human-verifiable contradiction. So one obvious direction to move in is to forget about bichromatic vertices now, and focus on finding the smallest configurations that can be shown to lead in a human-verifiable fashion to a contradiction. If for instance we can get as far as the showing that H1tri leads to a contradiction then we are done since there is a human proof on the wiki that H1tri occurs with positive probability.
) leads to a contradiction. The smaller graphs obtained more recently should be able to replace the three bichromatic hexagon pattern by a smaller pattern and still obtain a human-verifiable contradiction. So one obvious direction to move in is to forget about bichromatic vertices now, and focus on finding the smallest configurations that can be shown to lead in a human-verifiable fashion to a contradiction. If for instance we can get as far as the showing that H1tri leads to a contradiction then we are done since there is a human proof on the wiki that H1tri occurs with positive probability.
Yeah. However, I don’t think we currently have particular promising ways to find such things. I’m still rather enamoured of the bichromatic-vertex line of attack, actually, and not only because it seems quite promising for (computationally) excluding MCNP=5 – it also seems to me that these origin-forcing graphs could be particularly good building-blocks. We haven’t yet looked much at the colourings of these graphs (I mean standard colourings, where the origin has only one colour), but my gut feeling is that they are inherently more likely than the average graph to have useful features like virtual edges.
Also, hang on – do we in fact have a human-verified proof that having those three hexagons all 2tri leads to a contradiction? Surely the option has not been excluded (by the human proofs, anyway) that Tamas’s graph has colourings in which all three are 2tri but with different pairs of colours for different hexagons?
One small remark (coming from an attempt to remove measurability from the Falconer argument): let be a unit distance graph containing the origin in which the origin is known not to be bichromatic. Then, for any non-zero number z, if the points 0 and z are bichromatic, then the points v and v+z must also be bichromatic for some other vertex v in
be a unit distance graph containing the origin in which the origin is known not to be bichromatic. Then, for any non-zero number z, if the points 0 and z are bichromatic, then the points v and v+z must also be bichromatic for some other vertex v in  . I was hoping that this could be used to get some non-trivial upper bound on
. I was hoping that this could be used to get some non-trivial upper bound on  (the probability that 0 and z are monochromatic), but I don’t immediately see how to do so.
(the probability that 0 and z are monochromatic), but I don’t immediately see how to do so.
Nice – this seems to me to be a very promising “widget” to use in building something human-comprehensibly 5-chromatic! – maybe via probabilities, maybe even without. Please explain how you showed it. Also, just to be sure – you are using “bichromatic” in reference to a single point to mean “there exists a colouring of all other points in G that does not force the colour of that point” but you are using it in reference to a pair of points simply to mean that they are different colours, right? If so, different colours in all colourings of G or in a particular one? – because, do you mean “if the points 0 and z are different colours in all 4-colourings of G then the points v and v+z must also be different colours in all 4-colourings for some other vertex v in G”, or do you mean “if the points 0 and z are different colours in a particular 4-colouring of G then the points v and v+z must also be different colours in that same 4-colouring for some other vertex v in G”?
Either way, I believe we can use this result to build more-tightly constrained graphs from multiple copies of origin-forcing graphs. The existence of parallel virtual edges, whether “true” ones (the “all colourings” interpretation) or only simultaneously-occurring ones, leads to loads of promising-seeming constructions.
In fact I just realised that there is a third, even weaker interpretation of your words, namely that the identity of v is specific to a particular colouring, so that different colourings could use different v’s. Looking forward to your clarification.
Sorry, I meant the weakest of the statements you listed, namely if 0 and z have the same color, then there exists a vertex v in G such that v and v+z have the same color, but the choice of v depends on the coloring. Otherwise, the colorings of G and G+z would induce two colorings of G that agree everywhere except at the origin, which we know not to be the case.
Thanks. Hm, I’m still confused – this seems to lead to an absurdity, because we can only pick v from those vertices for whch v+z is also a vertex (right?). For example, consider any origin-forcing graph G with a vertex v at distance !=1 from 0, and add two new vertices at z and v+z that form a rectangle with 0 and v, such that |z| is longer than the Euclidean diameter of G. Then we’re not adding any edges at all, so the colours of the new vertices are unconstrained, but {v,v+z} is the only vertex pair between which the vector is the same as that of {0,z}, so whatever colouring we choose for G and z we need to use the same specific v and v+z.
So I think what you must be saying is an even weaker statement that I can’t articulate (and it’s probably no coincidence that I also can’t understand your “Otherwise” sentence). Help! – and apologies if I’m being dumb, which I feel I almost certainly am being.
I also don’t get it.
OK, let me try again:
Lemma Let G be a unit distance graph containing the origin, with the property that the origin cannot be bichromatic (thus, in any 4-coloring of G, the color of the origin is completely determined by the color of the other vertices of G). Then for any 4-coloring c of the plane and any complex number z such that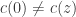 , there exists a non-zero vertex
, there exists a non-zero vertex  of
of  such that
such that  .
.
Proof Suppose this were not the case, thus there is a 4-coloring c and a complex number z such that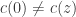 and
and 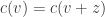 for all non-zero vertices
for all non-zero vertices  of
of  . Then if we define
. Then if we define  then we have two colorings
then we have two colorings 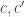 of
of  that agree at every vertex outside of 0, but disagree at 0, contradicting the hypothesis that the origin cannot be bichromatic in
that agree at every vertex outside of 0, but disagree at 0, contradicting the hypothesis that the origin cannot be bichromatic in  .
. 
Ah… I think my confusion arose from assuming that by “point” (in your original post) you meant “vertex in G” when in fact you meant merely a point in the plane that may or may not be a vertex in G. Right? So your assertion doesn’t say anything about G itself, only about G + (G+z), i.e. a graph G2 in which all the vertices v that are needed to make G origin-forcing have a counterpart vertex v+z. Now I get it! (But using it as a widget may be less easy than I’d hoped!)
A small point that may be useful: build a 36-vertex graph by adding to my 26er the vertices not already present that are reflections of existing ones in the line between vertices 11 and 17. This graph now has two forced vertices, namely 1 and 9. They rely on each other to be forced, but that still means that for any colouring of the other 34 vertices there are only four permitted colour-pairs that 1 and 9 can take, rather than 16. Since the minimal set of vertices that forces 1 and the minimal set that forces 9 have such a large intersection (14 vertices) there must be quite a tight constraint on how many colourings there are with 1 and 9 the same and with 1 and 9 different. It seems to me that we could probably obtain quite low numbers of admissible colourings by assembling copies of this in judicious ways. For example, rotating it 120 and 240 degrees around vertex 1 gives something with only 61 vertices (including all but three of Tamas’s original 43) in which four vertices are mutually forced, three of which are the unit triangle {5,9,16}. I guess that to push this all the way to a human-comprehensible disproof of CNP=4 we would need to find assemblages that minimise the mutuality of forcing while maximising the intersections of pairs of forcing sets, among other things. Could this approach lead to new probabilistic bounds?
Adapting this idea a little: my reduction of Tamas’s 43er to 26 demonstrates that the 42er obtained by deleting the origin contains at least six minimal origin-forcing subgraphs of order 25. (In practice I bet there are a lot more than that.) Now, an origin-forcing graph is one in which all colourings use at least three colours for the vertices at unit radius – of which there are 18 in the original 43er, and 14 in my 26er. Thus, there are at least six different always-trichromatic order-14 subsets of the original 18. Can we thence infer the presence of smaller always-trichromatic sets, without actually enumerating and inspecting the individual colourings? The motivation is that if we can get the always-trichromatic set down to just three vertices that are in an equilateral triangle, we are done, since two copies of it make a graph that can serve as my original M; and that possibly we can find origin-forcing graphs with intermediate numbers of vertices at unit radius that can human-comprehensibly serve as stepping-stones to such a graph.
I guess the first step would be to seek graphs that are human-comprehensibly origin-forcing but have fewer than 14 unit-radius vertices. (Jannis’s 26er has 14 too; his 24er only has 12, but we don’t yet have a human proof that it is origin-forcing.)
Ah, of course I overstated the requirement above: we only need to get to a never-mono triangle, not an always-tri one. The goal for always-tri can be the unit-radius trapezium, i.e. the hexagon minus two adjacent vertices; three copies of that suffice to exclude both 1tri and 2tri.
Anyway – how would the reduction work? First example: suppose we have two always-tri sets of size n that intersect in all but one each of their vertices. Then either the intersection is trichromatic or the other two vertices are mono, so we can spindle on those two and we’re down to n-1. We can’t iterate on this (not straightforwardly, anyway), but it might still be a useful widget.
Ah, of course we’re even done if a hexagon minus just one vertex can be made always-trichromatic, since 1tri has one of those that is bichromatic.
Here’s a somewhat speculative probabilistic thought that I feel may have a shot at both of our main goals, i.e. a human-comprehensible CNP lower bound of 5 and a computer-based lower bound of 6.
Marijn kindly shared with me a draft of his upcoming paper announcing 633, and one incidental observation he makes is that a ~400-vertex graph which he builds en route to the solution has (in the colourings he’s visualised) a non-randomly large proportion of monochromatic vertex pairs that are close together in the plane. This reminded me that I too had noticed this during my early explorations. In fact (and possibly this was because I was using a primitive backtracking algorithm rather than a SAT solver, but maybe not!), I observed it even more extreme form (and with even smaller graphs): In my case the region within about 1.5 of the origin often consisted almost entirely of totally monochromatic patches of diameter slightly less than 1. This tended to happen in graphs in the 100-vertex range and up that were built from my original V; other spindling distances such as 2 or 4 were not required.
I’m wondering whether this could be combined with the probabilistic approach. As Terry explained here:
we are done via the “dendrimer” construction if we have a graph more than half of whose vertex pairs at some defined distance no less than 1/2 are monochromatic in any colouring. We also know, as Terry noted here:
that we don’t need to stick to a single inter-vertex distance: we can take any set of distances for which the collection of vertex pairs at any such distance has this more-than-half-mono property, just so long as each distance is at least 1/2. In fact we can go further than that, because we can appeal to the generalised form of Lemma 17 and use distances shorter than 1/2 so long as in all colourings the proportion of mono pairs exceeds the corresponding probabilistic upper bound. Moreover, we can use some but not all pairs at a given distance.
I haven’t done any remotely rigorous analysis of whether this patchiness truly applies to all colourings of these high-edge-density, high-spindle-density graphs, but I feel it would be valuable to try to find that out. In the best case, we might find highly symmetrical graphs in the few-dozen-vertex range whose colourings are human-enumerable and checkable for a suitable “mostly-mono” property of some set of vertex pairs. And in the very best case, we might find some (large) 5-chromatic example whose patchiness as identified by eye suggests a suitable set of vertex pairs that can then be SAT-checked.
What do others think? Worth trying?
test
I had a look at the literature on chromatic number in higher dimensions. The most advanced paper seems to be this one
Click to access 1512.03472.pdf
It has some impressive lower bounds. I think I will add them into the Wiki. For a range of dimensions from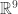 to
to  the best bounds come from a very simple graph construction on a sphere of radius
the best bounds come from a very simple graph construction on a sphere of radius 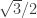 . They scale up by a factor of two so that the coordinates of the nodes of the graph have integer coefficients with three of them equal to
. They scale up by a factor of two so that the coordinates of the nodes of the graph have integer coefficients with three of them equal to 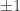 and the others zero. The edges of the graph then join points that are a distance apart of 2.
and the others zero. The edges of the graph then join points that are a distance apart of 2.
I am sure there should be scope for improving these results using other simple spherically symmetric constructions
Many thanks Philip. Concerning the scope for further improvements I’m strongly inclined to agree, but one person here, Dan, is much more likely to know (or to have reliable intuition) about that since he and Geoffrey Exoo have done lots of work on such bounds. Dan – what’s the status?
Actually my 60-vertex graph in R^3 is easily reduced to 59 (but I think no further) by rotating the clamps appropriately. The edge count is 183. A few months ago I also found (very provisional) upper bounds of 156 and 564 for R^5 and R^6 by the “permutohedron” approach with which Radoicic and Toth obtained 15 and 54. Finally: the other day I came across an assertion that the upper bound for R^4 has been reduced to 49, citing:
L. L. Ivanov. An estimate for the chromatic number of the space R^4.
Russian Math. Surveys, 61 (2006), 984-986
but I have not been able to obtain that paper, and since it’s weird for a result a decade old to be so seldom cited if it’s correct I’ve elected not to add it to the wiki for now.
For simplicity I’m just using this post as the reference for all the above.
After quick search, I was able to see the paper http://iopscience.iop.org/article/10.1070/RM2006v061n05ABEH004361/pdf
but its main result is the lower bound 7, not upper bound 49.
@Bogdam – many thanks – I can’t download the full text from there though – I would be grateful if you could please email the PDF to me at aubrey@sens.org – thanks!
I tried to reproduce the upper bound of 156 for R^5, but could only get 165. It is possible that I have a bug or missed a trick. Should we compare some numbers? I had 1984 dangerous neighbouring cells as defined by Radoicic and Toth, but not excluding negatives.
1984 neighbours is also what I had – 7882 for R^6. My coefficients for getting 156 were 14,30,38,42,55.
Further inspection of my old results reveals that 165 was the best I achieved with one coefficient being forced to be 1. Might that be the difference between our results?
I saw a lot of stochasticity in this computation. I had a few coefficient sets that got to 164, but the above coefficients were the only ones that beat 164, and I went up to a maximum coefficient of 80. Hence I would not be at all surprised if 156 can be beaten – and I would be astonished if 564 cannot be beaten – with more efficient implementations than mine.
OK I will do a more complete search at 156. There must a more efficient way to do this part. I think one of the numbers can be assumed to be a divisor of 156 but not necessarily equal to 1. I am working with coordinates on a plane in 6D so my coefficients will be different.
Your coefficient 55 is relatively prime to 156, and 55×139 is 1 mod 156, so if you multiply all your coefficients by 139 mod 156 you can get a set with a 1 in it.
Thankfully I have now managed to reproduce your best result of 156. My problem was that the coordinates I was using had some congruence relations that eliminated some options.
I will try to verify your R^6 result too but will need to do some optimisation first.
I see three main options for trying to improve these results, all of them quite difficult. It would be useful to know what Ivanov tried but I can’t access his paper either.
(1) non-linear colourings: In three dimensions this can’t help because each permutahedron touches 14 others face-on so 15 is a minimum for any colouring. However, in four dimensions each one touches 30 others which sets a minimum limit of 31 colours for this tessellation.
(2) alternative tesselations: I am looking at packings of 24-cells but the best colouring so far has 61 colours. Tesselations with two or more polytopes of very different sizes may be promising options.
(3) smaller cells: It is conceivable that if cells are reduced to less than half the size then some more optimal colourings are possible, linear or otherwise.
I don’t know how helpful it is, but the original Russian version seems to be available here: http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=rm&paperid=5396&option_lang=eng
Relying on Google translate, that paper does not demonstrate the 49 bound, but references the work of Coulson instead. The only Coulson paper cited does not include it.
@Emanuel – many thanks! Good to have that red herring out of the picture (though its origin remains quite intriguing!). The ratio of 54 to 15 is so high that one must be hopeful of finding a better polytope in R^4 (or, at Philip notes, a covering with >1 shape of polytope). If the more spherical the polytopes are, the better (which is surely a reasonable heuristic), it is worth noting that a covering of R^3 by two different polyhedra is known in which the mean surface/volume ratio is slighty less than that for the polytope:
https://en.wikipedia.org/wiki/Weaire%E2%80%93Phelan_structure
so there seems to be plenty to explore. Then again, even sphericality may be a misleading guide, seeing that the tiling of R^2 that I posted here:
has a “too-close neighbours” set of only 16 as against 18 for the hexagonal tiling, even though the tiles are quite a bit less circular than hexagons.
By “slighty less than that for the polytope” I of course meant “slightly less than that for the permutohedron”.
@ag24ag24 I wouldn’t go as far as saying sphericality may be a misleading guide, it appears to only get us so far if applied to just the regions themselves, but your pentagonal tiling does use a different kind of sphericality much stronger than the hexagons does, and that’s the sphericality of the exclusion zone.
The coloring using the bitruncated cubic honeycomb also exerts multiple relations to sphericality that aren’t obvious at first glance and which are not mentioned in the papers discussing these 15-colorings at all, which in fact I haven’t seen mentioned anywhere at all.
coloring using the bitruncated cubic honeycomb also exerts multiple relations to sphericality that aren’t obvious at first glance and which are not mentioned in the papers discussing these 15-colorings at all, which in fact I haven’t seen mentioned anywhere at all.
First there’s the compound dual tesselation (for lack of the existence or my knowledge of better notation) of the bitruncated cubic honeycomb, which is a rhombic dodecahedral honeycomb. Imagine taking a bitruncated octahedra as the starting cell, consider all cells that touch the base cell and take their centers as the vertices of the cell (a rhombic dodecahedron) that forms the compound dual tesselation, or whatever it is or should be called.
And for the dodecahedral honeycomb we know the relation to sphericality.
The coloring also exerts sphericality. Create a valid coloring of using the bitruncated cubic honeycomb, then take the centers of all cells of one color and connect them accordingly. The result is the tetrahedral-octahedral honeycomb, and its dual tesselation is again the dodecahedral honeycomb.
using the bitruncated cubic honeycomb, then take the centers of all cells of one color and connect them accordingly. The result is the tetrahedral-octahedral honeycomb, and its dual tesselation is again the dodecahedral honeycomb.
Following this I think that permutahedra in higher dimensions also exhibit more traits of sphericality, that could possibly even help addressing the sphere packing and kissing number problems but testing these ideas is out of my scope of ability and time for now. If this were to be the case I wouldn’t even know around how many corners and where exactly the correct tessellations may be hiding.
I’ve only very briefly read about the Phelan structure, but it does look promising for further research into these types of sphericality. The SketchUp plugin I’ve created to procedurally generate bitruncated cubic honeycombs could be adapted to create a Phelan honeycomb which could be pruned for interesting relations to sphericality and possibly a better coloring, but again there’s my time and money constraints. Though I might get at it some time in the future, after my current front with exclusion zones has progressed far enough.
ag24ag24, have you posted vertex coordinates for your 59-vertex graph anywhere?
Hi Ed – no, sorry, I have not taken the time to work them out. Of course they would anyway be somewhat arbitrary, because the three clamps can each rotate freely around the axis of the octahedron; getting down to 59 requires fixing two of the clamps, but there are masses of ways to do that (choices of which pair of vertices to make coincident). I’m not sure that the specification of a particular set of coordinates really adds much.
While I have your attention – can you tell us something about your exploration of highly edge-dense UD graphs in R^3 ? Long ago you posted a really neat one (basically a deformation of a cuboctahedron) on MO, and I am curious as to whether you discovered any other designs. Since my original breakthrough in R^2 was based on exploring graphs with high edge density, I’m keen to extend the idea to higher dimensions.
Can I post here?
This is the simplest unit-distance graph I could find that proves that the chromatic number of space is at least 6: (52 vertices and 166 edges) Does simpler graphs exist?
Consider first this 12 vertex graph:
Graph1:
Let A, Z and Æ be 3 same-colored vertices with the following coordinates:
A: (0, 0, 0)
Z: (sqrt(21/29), 13/sqrt(87), 0)
Æ: (-(15sqrt(87))/(48sqrt(7)+26sqrt(23)), (192sqrt(609)+59sqrt(2001))/(1152sqrt(7)+624sqrt(23)), (1/16)sqrt(51696sqrt(161)-655727))
Add the following 9 vertices:
B: (-(5sqrt(2001))/261, (40sqrt(87))/261, 0)
D: (0, sqrt(87)/6, 1/2)
E: (0, sqrt(87)/6, -1/2)
H: (sqrt(2001)/87, 13/(2sqrt(87)), 1/2)
I: (sqrt(2001)/87, 13/(2sqrt(87)), -1/2)
N: (-sqrt(23/87)/2+sqrt(3/58), (61+3sqrt(23/2))/(8sqrt(87)), (sqrt(23/2)-1)/8)
O: (-sqrt(23/87)/2-sqrt(3/58), (61-3sqrt(23/2))/(8sqrt(87)), -(1+sqrt(23/2))/8)
P: (-sqrt(23/87)/2-sqrt(3/58), (61-3sqrt(23/2))/(8sqrt(87)), (1+sqrt(23/2))/8)
Q: (-sqrt(23/87)/2+sqrt(3/58), (61+3sqrt(23/2))/(8sqrt(87)), (1-sqrt(23/2))/8)
We get 29 edges:
|ZD| = |ZE| = |ÆB| = |AH| = |AI| = |AN| = |AO| = |AP| = |AQ| = |BD| = |BE| = |BN| = |BO| = |BP| = |BQ|= |DE| = |DH| = |DP| = |DQ| = |EI| = |EN| = |EO| = |HI| = |HP| = |HQ| = |IN| = |IO| = |NO| = |PQ| = 1
This 12-vertex unit-distance graph can not be colored with less than 6 colors when A, Z and Æ have the same color. From this we can conclude that if a unit-distance graph contains a same-colored triangle with distances 2sqrt(2/3), 2sqrt(2/3) and sqrt(46)/4 then 9 vertices(and 29 edges) can be added to make sure you need at least 6 colors to color the graph.
Graph2:
Now, lets define the coordinates A, B, D, E, H, I, N, O, P and Q as before and define C and Ø like this:
C: ((5sqrt(2001))/261, (40sqrt(87))/261, 0)
Ø: (-(1517sqrt(2001))/120060, 5617/(480sqrt(87)), sqrt(11975617)/3680)
where
|CD|=|CE|=|BØ|=1
This 12-vertex unit-distance graph can not be colored with less than 6 colors when A, B and Ø have the same color. Conclusion: A triangle of same-colored vertices with the distances 5/3, 5/3 and (10sqrt(2001))/261 makes it possible to add 9 vertices(and 29 edges) so a unit-distance graph can be created that cannot be colored with less than 6 colors.
Graph3:
Finally we look at a 25 vertex graph. Define A, B, C, D, E, H, I, N, O, P and Q as before and add these 14 vertices:
F: (-sqrt(2001)/87, 13/(2sqrt(87)), 1/2)
G: (-sqrt(2001)/87, 13/(2sqrt(87)), -1/2)
J: (-sqrt(2001)/58, 163/(16sqrt(87)), 15/16)
K: (-sqrt(2001)/174, (35sqrt(87))/1392, 15/16)
L: (sqrt(2001)/58, 163/(16sqrt(87)), -15/16)
M: (sqrt(2001)/174, (35sqrt(87))/1392, -15/16)
R: (-(15sqrt(3/58)+7sqrt(23/87))/8, (419-(45sqrt(23/2)))/(64sqrt(87)), (15-sqrt(23/2))/64)
S: ((15sqrt(3/58)-7sqrt(23/87))/8, (419+45sqrt(23/2))/(64sqrt(87)), (15+sqrt(23/2))/64)
T: (sqrt(23/87)/2-sqrt(3/58), (61+3sqrt(23/2))/(8sqrt(87)), (1-sqrt(23/2))/8)
U: (sqrt(3/58)+sqrt(23/87)/2, (61-3sqrt(23/2))/(8sqrt(87)), (1+sqrt(23/2))/8)
V: (sqrt(3/58)+sqrt(23/87)/2, (61-3sqrt(23/2))/(8sqrt(87)), -(1+sqrt(23/2))/8)
W: (sqrt(23/87)/2-sqrt(3/58), (61+3sqrt(23/2))/(8sqrt(87)), (sqrt(23/2)-1)/8)
X: ((15sqrt(3/58)+7sqrt(23/87))/8, (419-45sqrt(23/2))/(64sqrt(87)), (sqrt(23/2)-15)/64)
Y: ((-15sqrt(3/58)+7sqrt(23/87))/8, (419+45sqrt(23/2))/(64sqrt(87)), -(15+sqrt(23/2))/64))
We get 79 edges:
|AH| = |AI| = |AN| = |AO| = |AP| = |AQ| = |BD| = |BE| = |BN| = |BO| = |BP| = |BQ|= |DE| = |DH| = |DP| = |DQ| = |EI| = |EN| = |EO| = |HI| = |HP| = |HQ| = |IN| = |IO| = |NO| = |PQ| = |CE| = |DE| = |CT| = |CU| = |CV| = |CW| = |DF| = |DT| = |DU| = |FG| = |AF| = |FT| = |FU| = |AT| = |AU| = |TU| = |EG| = |EV| = |EW| = |GV| = |GW| = |AG| = |AV| = |AW| = |VW| = |BJ| = |BR| = |BS| = |JD| = |JK| = |JR| = |JS| = |HK| = |AK| = |KR| = |KS| = |AR| = |AS| = |RS| = |CL| = |CX| = |CY| = |EL| = |LM| = |LX| = |LY| = |GM| = |AM| = |MX| = |MY| = |AX| = |AY| = |XY| = 1
A 4-coloring of this 25 vertex graph is impossible and a 5-coloring is only possible if we find a same-colored triangle in either A,B and C or in A,D and L or in A,E and J. Since these triangles are of the 2 types previously mentioned it is clear that we kan add 9×3 vertices to this 25 vertex graph and get a 52 vertex graph which requires at least 6 colors for a vertex coloring of the graph.
.
file:///C:/Users/Asger/OneDrive/Skrivebord/graph1.png
file:///C:/Users/Asger/OneDrive/Skrivebord/graph2.png
file:///C:/Users/Asger/OneDrive/Skrivebord/graph3.png
file:///C:/Users/Asger/OneDrive/Skrivebord/graphfinal.png
Asger – many thanks for this excellent discovery! I believe I have improved it to 47 vertices. Please see my post in the most recent, i.e. current, thread (thread 17):
For anyone looking at this page then this is the updated version of my graph showing just the scaffold. I realized that I did not need J,K,R and S so i removed them and we still have a graph where a 5 coloring will ensure that one out of three triples are monochromatic. The triple A,E and J is replaced with the triple C, F and M. The final graph ends up being a 48 vertex graph.
I have reduced the upper bound for R^6 to 484 using the permutahedron and a linear colouring scheme. I can’t rule out any smaller numbers yet.
Now I reduced it to 483. The coefficients were 1 203 277 308 357 371.
Thanks Philip. Yeah, the reason I noted that I’d be astonished if 564 were optimal was that my ratherinefficient implementation only barely went high enough in coefficients to find any solutions at all. I’m presuming you succeeded in greatly optimising yours.
Did you hammer R^5 like hell without improving on 156 ?
Yes, I found a couple of optimisations and can confirm quite quickly that 156 is the best possible by this means. I have R^6 down to 472 now with coefficients 1 90 100 232 237 314. I wont be able to cover all possibilities though.
I agree that looking at different honeycomb structures is important for higher dimensions. For six dimensions the best upper bound I have is now 462 colours using the permutahedron with a linear colouring. The coefficients were 331 161 67 49 385. I can’t do an exhaustive search but have checked most possibilities down to 450 without any luck and will soon give up.
There is a big gap between upper and lower bounds which begs the question as to which is likely to be nearer the correct figure. In other problems where there are bounds there is usually at least some numerical evidence of where the correct numbers lie but with this problem that does not seem possible.
To get lower bounds for R^5 upwards it is not hard to think of graphs that might do well. The difficulty is to prove it given the computation required to find the chromatic number. In higher dimensions most records are set by finding the size of the biggest independent set . Then the chromatic number is at least
. Then the chromatic number is at least  . This seems to give an efficient lower bound on the chromatic number for a given graph
. This seems to give an efficient lower bound on the chromatic number for a given graph 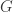 but computing
but computing  is still NP hard. The key seems to be finding cases where this is easier.
is still NP hard. The key seems to be finding cases where this is easier.
For simplicity I looked at the sub-problem of finding the chromatic number for a simple hypercubic lattice of dimension but with the distance between cells set at
but with the distance between cells set at 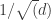 for integers
for integers 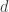 . The best lower bounds for
. The best lower bounds for 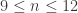 come from simple graphs in these lattices with
come from simple graphs in these lattices with  so this is not a trivial problem.
so this is not a trivial problem.
For odd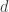 the lattice is bipartite so only even numbers are of interest. Solving the problem for
the lattice is bipartite so only even numbers are of interest. Solving the problem for 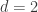 is equivalent to finding the most efficient binary codes of length
is equivalent to finding the most efficient binary codes of length  and depends on the independent set of the n-half cube which is known up to 16 dimensions as sequence A005864. For larger
and depends on the independent set of the n-half cube which is known up to 16 dimensions as sequence A005864. For larger 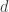 less is known.
less is known.
I think understanding this better would help even with just the 2 dimensional case since the rings also take the form of hypercubic lattices in higher dimensions.
Many thanks Philip. That’s only five coefficients – was the other one 1 as in your earlier reports?
I’ve been trying to identify tesellations in R^3 and up that have a smaller “forbidden cells” set than the permutohedron, but without success – frustrating, since it can rather easily be done in R^2 as I noted earlier. I’m trying to conceptualise a finite-element approach of the sort that Dustin proposed for the Pritikin problem, but I’m not making it work.
Yes, there was also a coefficient of 1 that I should have included, good spot.
There is still some slow, but steady progress in finding a smaller unit-distance graph with chromatic number 5. I have it now down to 610 vertices and 3000 edges. The image below shows this graph.
Many thanks Marijn. Everyone: I expect you will immediately see that this colouring quite strongly exemplifies the patchiness that I discussed yesterday. It seems, in fact, that there is an even more extreme “occult patchiness” going on here that is not immediately visible by eye but could still do what’s needed as described in my post yesterday. Watch this space 🙂
Intriguing to see such patchiness arise so early. I had expected to see exactly this behaviour some time later down the road, in a 7-color or 6-color graph with accordingly high vertex counts, but I certainly didn’t expect to see this in a 5-color graph.
One of the things I’ve found during my work on the exclusion zone is that there’s inherent inefficiency to finely dispersing colors in the first ring around a vertex, because that in turn means some of those secondary exclusion zones won’t get to overlap each other, so this patchiness might be a ramification of that. But I’m still rather skeptical of that since I’d expect this to only start mattering quite a bit later. I don’t have anything nice on that front written up yet, though I’ll focus more on that and post what I have later.
And I’m certainly watching to find out about this “occult patchiness”.
Although I did not force the patchiness, I did force all vertices apart from the origin to be colored with 4 colors. Without that restriction the patchiness would disappear.
Just as I would expect, and as we can see in earlier 5-chromatic graphs easing the restrictions also makes the patchiness disappear. I’ve just realized how the same kind of patchiness even occurs in the 3-chromatic example of a 2-ball subset of space as the diameter of this 2-ball approaches 1 from above. I had mentioned this in one of the earlier posts.
It very much seems like this is part of the link from most efficient tesselations of a space to most efficient unit distance graphs embedded in this space, both of these providing upper and lower bounds that agree on and prove the chromatic number of the space.
I’m currently writing up an example of a 2-chromatic expanded graph, a supspace of the plain where this agreement of tesselation and embedded unit distance graph becomes very clear.
It now also strikes me how roughly this will work when the diameter of such a 2-ball first allows for a 2-simplex to be embedded, at which point the tesselation jumps to 4 colors, and most likely the embedded unit distance graph as well. Using many such simplexes will then probably result in patchiness of 3 colors while forcing some node into the first color.
This makes me wonder just how generalized this works. At a glance it would appear the same holds true not just for complete but also for partial spaces, maybe even spaces with completely different geometry such as a hyperbolic space.
Yes – patchiness is, indeed, not to be expected except in conditions where the graph is fairly difficult to colour at all – which, of course, depends on how many colours one is using and also things like restricting to having one colour used for only one vertex.
Do we have a solid grasp of what restrictions yield patchiness and in which way?
To my knowledge there are at least 3 definite factors which we can push to varying degrees for patchiness to occur, that is space, vertex count and colors. We always have to push colors down. Maybe for finite vertex count graphs we need to force it in the way Marijn did here, origin point with a starting color and the rest with as few other colors as possible, but I’m not sure about that.
My example with odd cycle graphs shows effects of applying space restrictions, the 610 vertex graph is clearly pushing the maximum vertex count down.
As I’ve conjectured the same patchiness will probably force us into using Jordan curve bounded areas, or manifolds that are homeomorphic to their containing space.
My recent post on expanded graphs (for lack of knowing any other notation) already shows an entire class of examples of this in an extreme manner.
The TL;DR: of that article is as follows: Take an euclidean space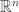 , embed a restrictive valid unit distance graph, expand the nodes to n-balls, without the exclusion zones touching areas of previously unconnected nodes. This class of subspaces of
, embed a restrictive valid unit distance graph, expand the nodes to n-balls, without the exclusion zones touching areas of previously unconnected nodes. This class of subspaces of 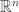 will then:
will then:
1. Have a clear defined minimum amount of needed colors as defined by the unit distance graph we started with.
2. Have a clear defined maximum amount of needed colors that agrees with the minimum, as defined by filling the areas with colors we already have from the unit distance graph.
3. Depending on how restricted the original unit distance graph was, the resulting subspace will have some n-balls that have to be entirely single-colored, with a clearly defined n-volume. Using lower dimensional areas or non-measurable sets is provably out of the question, as is fine dispersal of colors.
I think the patchiness seen in this class of subspaces is the same we see in the 610 vertex graph. And I would reckon this patchiness will apply to the entire space with the color restriction alone, as the exclusion zone will become more and more restrictive in turn.
If you highlight the areas of different colour they are seen to form a hexagonal pattern with colours repeating in cycles of two in each of three directions. This is a close shot a four-colouring the plane if areas near edges and vertices of the hexagons are ignored.
If you 4-colour the whole ring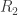 you will not get any patchiness. This is because 4-colourings of
you will not get any patchiness. This is because 4-colourings of 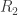 has periodicity 8. I.e. for any 4-colouring
has periodicity 8. I.e. for any 4-colouring 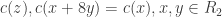 . Since
. Since  is in the ring for all integers
is in the ring for all integers 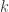 this means there are arithmetic progressions of monochromatic points with arbitrarily small spacing along any straight line.
this means there are arithmetic progressions of monochromatic points with arbitrarily small spacing along any straight line.
Philip – sure, and that probably says something about the circumstances under which we could obtain really extreme (close to limiting) patchiness. However, the situation of interest here is not that – it is the circumstances under which we would have sufficient patchiness (in all colourings) to activate the probabilistic approach and the dendrimer construction. Our current upper bounds on short distances become weaker for shorter distances, but I’m cautiously optimistic that we might find 5-chromatic graphs in which more than 2/3 of the vertex pairs at distances between (say)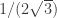 and 2/5 are mono in any colouring. I expect that they would be quite large, but maybe not infeasibly so.
and 2/5 are mono in any colouring. I expect that they would be quite large, but maybe not infeasibly so.
Best known results table in the Wiki hasn’t been updated.
Don’t recall seeing this paper by Schwartz referenced, but the idea is reminiscent of the work you folks have been doing.
Click to access 1211.4948.pdf
This paper by Schwartz, Solymosi and de Leeuw might also be of interest.
https://arxiv.org/abs/1008.3671
What is known about the set of unit distance graphs as a whole? It seems plausible to me (if fiddly to prove) that every unit distance graph can be embedded with its vertices in the set of constructible numbers (in the sense of compass as straightedge). But that’s probably too generous. Consider a complex number such that there is a unit distance graph
such that there is a unit distance graph  with two connected vertices
with two connected vertices  and
and  such that in any embedding of
such that in any embedding of  into
into  in which
in which  is placed at 0 and
is placed at 0 and  is placed at 1, some vertex of
is placed at 1, some vertex of  must be placed at
must be placed at  . Now consider the set
. Now consider the set 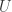 of all such
of all such  . The set
. The set 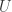 is a set of points “necessary” for unit distance graphs (fixing nodes at 0 and 1 to eliminate symmetry). It again seems plausible to me that
is a set of points “necessary” for unit distance graphs (fixing nodes at 0 and 1 to eliminate symmetry). It again seems plausible to me that 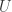 is sufficient in the sense that every unit distance graph can be embedded with its vertices in
is sufficient in the sense that every unit distance graph can be embedded with its vertices in 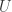 .
. 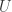 is no doubt also a ring, etc.
is no doubt also a ring, etc. 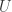 contains the Eisenstein integers, but it’s not even clear to me whether
contains the Eisenstein integers, but it’s not even clear to me whether 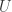 contains
contains  !
!
On the upper bound of CNP side, I vaguely recall some results about the “raggedness” of six-colorings — that seven was the best you could do with a “nice” “tile-like” coloring of the plane. I don’t remember the exact definition of nice, so I’ll hazard one of my own: there exists a bidirectional increasing sequence of open sets of
of open sets of  such that for each
such that for each  , if
, if  is monochromatic and
is monochromatic and  .
.  potentially empty for all but finitely many
potentially empty for all but finitely many  ; I’m not picky. I would just use a partition into open sets, but I have to handle the boundaries somehow. Anyway, is seven known to be the best for such a coloring?
; I’m not picky. I would just use a partition into open sets, but I have to handle the boundaries somehow. Anyway, is seven known to be the best for such a coloring?
Here’s a variation on origin-forcing. Can we find a reasonably small graph that contains a triangle of side 1 and its centre and forces the centre to be the same colour as one of the triangle’s vertices? It feels like that should not be very much harder than origin-forcing, so maybe it can be done human-comprehensibly. First, though, would it lead to a proof of CNP >=5? It would show that is exactly 1/3, which seems like a mighty good start, but I haven’t yet been able to complete a proof.
is exactly 1/3, which seems like a mighty good start, but I haven’t yet been able to complete a proof.
Exoo-Ismailescu preprint published on arXiv studying two forbidden distances:
https://arxiv.org/abs/1805.06055
They mainly construct small graphs of that require 5 colors such that every distance is 1 or d. I kind of missed mentioning two problems. The first is whether excluding an arbitrarily small d can change the chromatic number, and the second is whether excluding a transcendental d can change the chromatic number, see Bukh:
https://arxiv.org/abs/math/0703856
I’ve translated the Exoo-Ismailescu arguments to probabilistic language and put them on the wiki.
Thanks Terry. Note my improvement of Lemma 23 to 1/6 here:
Wow – I’m particularly excited by Section 6. (I mean, the other graphs are really cool too, and I would love to know how Dan and Geoffrey found them – and also I feel super-dumb for not noticing earlier that my so-called new distance is the same as the distance
is the same as the distance  that Dan listed in his earlier post… but the technique in Section 6 seems to be insanely powerful. I am wondering whether it might already be possible to prepare the ground for disproving CNP=5 by identifying some {d,d’} pairs for which the technique of Section 6 can be demonstrated, so as to give some candidates for distances that can eventually serve the role analogous to
that Dan listed in his earlier post… but the technique in Section 6 seems to be insanely powerful. I am wondering whether it might already be possible to prepare the ground for disproving CNP=5 by identifying some {d,d’} pairs for which the technique of Section 6 can be demonstrated, so as to give some candidates for distances that can eventually serve the role analogous to  in Dan and Geoffrey’s earlier paper.
in Dan and Geoffrey’s earlier paper.
I was thinking about Tamas’s computer assisted result in https://dustingmixon.wordpress.com/2018/05/05/polymath16-fourth-thread-applying-the-probabilistic-method/#comment-4366 that gives only finitely many ways to 4-color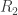 , all of which make the induced coloring of
, all of which make the induced coloring of  periodic; from this one easily shows that CNP is at least 5. One way to approach a human proof of this result is to impose some initial symmetry hypothesis on the coloring. For instance one could restrict attention to 4-colorings c of
periodic; from this one easily shows that CNP is at least 5. One way to approach a human proof of this result is to impose some initial symmetry hypothesis on the coloring. For instance one could restrict attention to 4-colorings c of 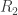 which are periodic with periods
which are periodic with periods  , thus
, thus 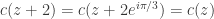 for all
for all  . Can one then control the possible 4-colorings of
. Can one then control the possible 4-colorings of 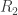 ? With this particular periodicity hypothesis, each coset of
? With this particular periodicity hypothesis, each coset of  has only
has only  colorings, so it is tempting to think of
colorings, so it is tempting to think of 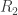 as a whole bunch of
as a whole bunch of  ‘s stacked together and the problem becomes that of 24-coloring the quotient lattice
‘s stacked together and the problem becomes that of 24-coloring the quotient lattice 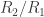 with some moderately complicated rules about what adjacent colors. Note that Tamas already did not need the full ring
with some moderately complicated rules about what adjacent colors. Note that Tamas already did not need the full ring 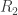 , only a bounded number of powers of
, only a bounded number of powers of  were actually used (maybe the powers between
were actually used (maybe the powers between 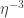 and
and 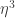 , if I read his construction correctly).
, if I read his construction correctly).
The quotient group still contains lattices isomorphic to
still contains lattices isomorphic to  as a group, i.e. the lattices generated by
as a group, i.e. the lattices generated by  and
and 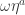 for a fixed
for a fixed  not equal to zero. These have to be coloured with the 24 permutations of four colours such that no two connected permutations have a colour in the same place. This is also equivalent to finding four 4-colourings that never clash.
not equal to zero. These have to be coloured with the 24 permutations of four colours such that no two connected permutations have a colour in the same place. This is also equivalent to finding four 4-colourings that never clash.
No periodicity constraint has been applied to these lattices, but colourings are further constrained by the relationships between and
and  .
.
I think this approach is worth trying, but instead of perodicity I suggest
I suggest 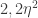 or
or 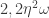 . Tamas found periodicy of 2 in
. Tamas found periodicy of 2 in  but only in one direction. I think these suggestions better reflect that. It enforces the periodicity of 2 in one direction on 2 different
but only in one direction. I think these suggestions better reflect that. It enforces the periodicity of 2 in one direction on 2 different  sub-lattices.
sub-lattices.
It would be good to understand if this periodicity of 2 leads to a periodicity of 8 in other directions. We know from Aubrey’s original work that no hexagon has a monochromatic triangle. I think you can get from there to the periodicity 2 in one direction on with a human proof. It would be good to get from there to periodicity 8 by human proof. Has that been achieved yet?
with a human proof. It would be good to get from there to periodicity 8 by human proof. Has that been achieved yet?
With periodicity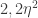 the lattice generated by
the lattice generated by 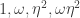 looks like an infinite matrix to be coloured with four colours. The edges given by these four generators plus
looks like an infinite matrix to be coloured with four colours. The edges given by these four generators plus  and
and 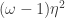 imply that this matrix is tiled with 4 by 4 Latin squares that overlap half way in both directions. There are only a few inequivalent Latin squares so this is not hard to analyse by hand.
imply that this matrix is tiled with 4 by 4 Latin squares that overlap half way in both directions. There are only a few inequivalent Latin squares so this is not hard to analyse by hand.
These arrays of Latin squares are then further constrained by the edges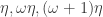 . These can be expressed in terms of $ the generators already used. This forces other elements of the matrix to take different colours. I don’t think that is enough to get the desired result, but it may be possible to include more powers of
. These can be expressed in terms of $ the generators already used. This forces other elements of the matrix to take different colours. I don’t think that is enough to get the desired result, but it may be possible to include more powers of  .
.
I’ve been working a little bit to try and figure out whether the only 5-colorings of are linear. (See here https://dustingmixon.wordpress.com/2018/05/05/polymath16-fourth-thread-applying-the-probabilistic-method/#comment-4307 ). I didn’t get that far, but I may as well record what I’ve done:
are linear. (See here https://dustingmixon.wordpress.com/2018/05/05/polymath16-fourth-thread-applying-the-probabilistic-method/#comment-4307 ). I didn’t get that far, but I may as well record what I’ve done:
(1) I took Phillip Gibbs linear 5-coloring of and checked that, for each color pair, the induced subgraph on those two colors is connected. If this weren’t true, I could switch colors on one component and not another and get a 5-periodic coloring which would probably not be linear. No luck, they are connected.
and checked that, for each color pair, the induced subgraph on those two colors is connected. If this weren’t true, I could switch colors on one component and not another and get a 5-periodic coloring which would probably not be linear. No luck, they are connected.
(2) In order to do this, I had to make explicit a bunch of Phillip Gibbs computations, which I might as well spell out for the record. Let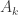 denote the ring
denote the ring ![\mathbb{Z}[\sqrt{5}]/\sqrt{5}^{k+1}](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%5Csqrt%7B5%7D%5D%2F%5Csqrt%7B5%7D%5E%7Bk%2B1%7D&bg=ffffff&fg=303030&s=0&c=20201002) and let
and let ![B_k = A_k[\sqrt{-3}]](https://s0.wp.com/latex.php?latex=B_k+%3D+A_k%5B%5Csqrt%7B-3%7D%5D&bg=ffffff&fg=303030&s=0&c=20201002) . For any
. For any 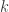 , we can identify
, we can identify 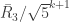 and
and 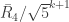 with
with  . (There is more than one way to do this. I want to send
. (There is more than one way to do this. I want to send  in
in  to
to  .) The unit elements of
.) The unit elements of  , and
, and 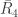 , map to
, map to  . One of Gibbs 5-colorings is to color
. One of Gibbs 5-colorings is to color  by
by  . I think (but am not certain), that all the others are related to this by
. I think (but am not certain), that all the others are related to this by  symmetries.
symmetries.
I’d love to figure out a way to tackle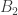 (so, quotienting by
(so, quotienting by  instead of
instead of  .) But a 390, 625 vertex graph is really big! Any suggestions for how to do it?
.) But a 390, 625 vertex graph is really big! Any suggestions for how to do it?
One thing I learnt from looking at how they build examples for higher dimensions is that sometimes it may be better and sufficient to look for independent sets on the graph, rather than full colourings.
I’ve temporarily dropped my earlier attempts at finding a proof for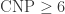 in favor of a cleaner approach, and I’m also more confident in this one. It uses the De Bruijn–Erdős theorem, exclusion zones and expanded graphs to rule out any possibility of not using regions bounded by Jordan curves, and Woodall (later on Coulson as well) already proved that with such regions
in favor of a cleaner approach, and I’m also more confident in this one. It uses the De Bruijn–Erdős theorem, exclusion zones and expanded graphs to rule out any possibility of not using regions bounded by Jordan curves, and Woodall (later on Coulson as well) already proved that with such regions 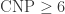 , so taking these into account this is a human-verifiable proof for
, so taking these into account this is a human-verifiable proof for 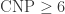 . The actual version is more generalized and applies to higher dimensions too, but I’m not aware of the ramifications on lower bounds in higher dimensions.
. The actual version is more generalized and applies to higher dimensions too, but I’m not aware of the ramifications on lower bounds in higher dimensions.
It is not an example of an actual unit distance graph with chromatic color 6 however, nor does it give any real hints (that I see) for how to get such a graph.
Short version: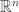 unit distance graphs where
unit distance graphs where 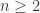 .
.
Let’s assume the use of single-colored regions homeomorphic to their containing space, that is Jordan–Brouwer separated spaces, is avoidable for the most efficient coloring in
The De Bruijn–Erdős theorem implies that there is a finite critical unit distance subgraph of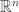 . This subgraph can be embedded and expanded in
. This subgraph can be embedded and expanded in 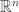 resulting in a subset of
resulting in a subset of 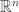 .
.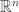 without such regions the same has to apply to this subset. Analyzing two n-balls in range of one another with exclusion zones we find that there’s just one way of efficiently resolving their relation which is by assigning one color per n-ball. This contradiction proves that the use of such regions is unavoidable during the hunt for the chromatic number of euclidean unit distance graphs.
without such regions the same has to apply to this subset. Analyzing two n-balls in range of one another with exclusion zones we find that there’s just one way of efficiently resolving their relation which is by assigning one color per n-ball. This contradiction proves that the use of such regions is unavoidable during the hunt for the chromatic number of euclidean unit distance graphs.
If it’s possible to color
It does not prove that a coloring of the entirety of the plane has to consist of Jordan curve bounded regions, as some stray points or lines are permissible, though demonstrably useless.
I see multiple ways of verifying this result from different angles too. For one there’s what I’d call over-exclusion, but I’m neither equipped to attempt that in the general case, nor do I see any good reason to do so in the first place.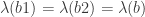 . The considered space has a measure of
. The considered space has a measure of 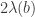 , and the total effective exclusion zone of a 2-coloring has the same measure. The exclusion zone of any vertex inside of a Jordan–Brouwer boundary is a subset of the exclusion zone of the boundary itself, so just the boundary of one of the n-balls already has an exclusion zone with measure
, and the total effective exclusion zone of a 2-coloring has the same measure. The exclusion zone of any vertex inside of a Jordan–Brouwer boundary is a subset of the exclusion zone of the boundary itself, so just the boundary of one of the n-balls already has an exclusion zone with measure  . We can also take a line that goes through the center of both n-balls and consider it’s intersection with one of the n-balls, and it’s exclusion zone also has measure
. We can also take a line that goes through the center of both n-balls and consider it’s intersection with one of the n-balls, and it’s exclusion zone also has measure  . If we color these two 1-dimensional subsets in one n-ball differently we already get a total effective exclusion of more than just
. If we color these two 1-dimensional subsets in one n-ball differently we already get a total effective exclusion of more than just 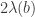 , and a valid 2-coloring becomes impossible, that is our space is over-excluded. The same will hold for attempted colorings with 0-dimensional sets such that no 1-dimensional set can be discerned via path connectedness, which would then branch over into my thoughts on topological contradictions of such colorings.
, and a valid 2-coloring becomes impossible, that is our space is over-excluded. The same will hold for attempted colorings with 0-dimensional sets such that no 1-dimensional set can be discerned via path connectedness, which would then branch over into my thoughts on topological contradictions of such colorings.
But the 2 n-ball example can give us a decent look at that in this specialized case, let’s name the balls b1 and b2. They have the same measure
I’ll see about getting this into a paper, possibly on arXiv, but that’ll take time.
Hello Bernhard, Woodall did not prove it – Townsend pointed out Woodall’s mistake and found his own proof of CNP being least 6 for map-type coloring.
Coulson is from a different opera: he proved that the upper bound for CN of 3-space is 15.
Details in my “Mathematical Coloring Book.”
Hi Alexander,
That was also my understanding (from your book and elsewhere), but actually it seems that Coulson did also do the thing Bernhard mentions: J. Aust. Math. Soc. 77 (2004), 191–196. This is much more recent than Townsend or Woodall, of course, and he doesn’t reference them, so maybe he really didn’t know of the earlier work, but also maybe he is defining “map-type” in a slightly inequivalent way (I can’t firmly decide). I will email you the paper.
I wasn’t aware that Townsend was involved with Woodall’s 1973 work like that, so thanks for pointing that out. But I knew of Coulson’s work on upper bounds, that was one of the most inspiring works to me on this problem, and I kept coming back to it many times throughout the months.
Unfortunately the cost of your book is currently prohibitive to me so I stuck to going through all the completely free work available, though I should be able to get my hands on it within the next 2 months.
For clarification, I came across these references on Wikipedia, which while mentioning the newer Coulson paper never even references Townsend in the first place, I’ve only found some of his work through these threads and obviously missed out somewhere.
Has there really been no comments for so many days or did something go wrong with moderation? I’ve been busy with trying to prove that we can suppose that the origin is bichromatic and falling deeper and deeper into the rabbit hole:
https://mathoverflow.net/questions/300604/almost-monochromatic-point-sets
Okay, moderation is off again – that answers my question…
I kinda just assumed we all sunk into our own respective rabbit holes. I’m still busy trying to get my paper on Jordan-Brouwer separation together, but will probably take another week or so at least.
I think I’ve started to get some first solid grasps on where this patchiness comes from exactly too.
Path, color and graph connectedness and their relation so far seem very decent at both predicting and explaining some fundamental rules of coloring, and not just for unit distance graphs.
On an intuitive level this works for finite unit distance graphs too, but I’m not sure how to rigurously test and formalize this. It looks like the exclusion zone sort of indirectly enforces topological rules of the containing space but that’s washy at best, and misinterpretation of some results at worst. Time and some more work will hopefully tell.
I am trying to understand the general principles underlying the “unplanned edges” that we’ve been seeing here and there, and I am floundering. What I mean is: can we give a general statement of “why” (for example) the red edge in Tamas’s construction:
https://htamas.ces.hu/files/cnp/implunit/
has length exactly 1? I restrict myself to Minkowski sums of only two sets of unit vectors, so I think what I’m asking is: in a pentagon , where
, where  are all products of at most two
are all products of at most two 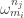 for integers
for integers  (k typically 2, I guess, but 1 would be a great start!), when (in closed form) does
(k typically 2, I guess, but 1 would be a great start!), when (in closed form) does  ?
?
I note that in Tamas’s case we have the interesting cycle . Does this cycle work only because 1+3=4?
. Does this cycle work only because 1+3=4?
Yes!
I can’t really tell what’s going on anyway, but as long as the others can. My personal tip is to make a free wordpress account, there you can test your syntax before posting as the backend features a preview.
(I don’t get why there’s no preview function for frontend comments but eh…)
Though my earlier posts also contain some bad errors, but I doubt there’s much of a point in me fixing them now, not before I don’t have my exclusion zone analysis done and out.
Gah… m_i a positive integer, n_j between -k and k, and i and j indexing m and n respectively. I must get more sleep…
Good question. The set of elements of unit modulus in the ring can be generated multiplicatively from 4 primitives
can be generated multiplicatively from 4 primitives 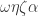 as given the in the Wiki at the bottom of http://michaelnielsen.org/polymath1/index.php?title=Algebraic_formulation_of_Hadwiger-Nelson_problem but that does not answer the question.
as given the in the Wiki at the bottom of http://michaelnielsen.org/polymath1/index.php?title=Algebraic_formulation_of_Hadwiger-Nelson_problem but that does not answer the question.
How do you find all combinations of five unit vectors that form a closed loop? I can’t think of any way to answer this other than to generate the units and search brute force for the loops.
Thanks Philip. The interesting case is where four of the five are members of a small set defined as above (i.e., with only two or three different m’s) but the fifth is not. (This is the situation in Tamas’s example, no?)
I have a partial explanation for why this happens. Use these numbers:
Work out this expression
So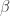 has unit modulus. It is inevitable that this would reduce to a simple expression but I can’t see a simple condition for it to have unit modulus.
has unit modulus. It is inevitable that this would reduce to a simple expression but I can’t see a simple condition for it to have unit modulus.
Multiply by to get the expression for the “unplanned edge” corresponding to the diagram.
to get the expression for the “unplanned edge” corresponding to the diagram.
So in terms of the four generators of unit vectors in the ring the unplanned edge is given by
OK… so can we still do this if we instead define as
as  ? I’m trying to maintain a visualisable equivalence in my head between the algebraic and geometric descriptions of these things, so here I’m trying to keep all of
? I’m trying to maintain a visualisable equivalence in my head between the algebraic and geometric descriptions of these things, so here I’m trying to keep all of 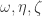 be anticlockwise rotations of (1,0) by a spindling distance of 1,
be anticlockwise rotations of (1,0) by a spindling distance of 1, 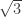 and 2 respectively. I think my question is, can your
and 2 respectively. I think my question is, can your  be expressed as a product of powers (not just as a sum of four products of powers) of
be expressed as a product of powers (not just as a sum of four products of powers) of 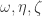 ? Where does
? Where does 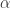 come from in spindling terms, as opposed to ring terms?
come from in spindling terms, as opposed to ring terms?
Also, “sums of at most two” should of course have been “products”.
Thanks for these questions which I will try to answer one at a time.
If you use your alternative definition of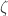 you are introducing an extra factor of
you are introducing an extra factor of  . Since complex conjugates are also included the number
. Since complex conjugates are also included the number 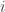 itself can be generated in the ring as
itself can be generated in the ring as  , so your version of the ring would include extra 90 degree rotations that we don’t need. The definition I gave avoids this.
, so your version of the ring would include extra 90 degree rotations that we don’t need. The definition I gave avoids this.
Remember that because we are using complex numbers there is a duality between rotations and vectors of unit length which are both represented by complex numbers of unit modulus. The two things are just different roles of the same numbers used either additively or multiplicatively. This is one of the properties that makes the algebraic approach so powerful.
As far as I know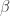 (or
(or 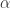 ) cannot be thought of as coming from a spindling operation as we have defined them so far, but they do appear if you form a triangle with edges of length 4, 4 and 3. There may be other geometric constructions but perhaps the “unplanned edge” is the best way to think of it.
) cannot be thought of as coming from a spindling operation as we have defined them so far, but they do appear if you form a triangle with edges of length 4, 4 and 3. There may be other geometric constructions but perhaps the “unplanned edge” is the best way to think of it.
Many thanks Philip – this is very helpful. Your last paragraph sums it up – it cannot be a coincidence that (a) these new angles emerge from spindling at length 4/3 and (b) various of our graphs force vertices 8/3 apart to be the same colour. Even if there is no closed-form answer to my original question about pentagons, maybe the brute-force search for such loops (which would not be all that onerous – I bet even heptagons could be enumerated) can identify rotations that would generate a helpful density of unplanned edges. Maybe we’ve already exhausted that possibility in the world where the initial distances are defined by the triangular grid, but I’m thinking it could be a promising way to evaluate completely novel starting-points, such as the regular pentagon/decagon that I discussed recently.
PS: perhaps I should clarify precisely what I meant by “closed form”. I’m thinking of a parametrisation, in the same kind of sense as that of Pythagorean triples. It could be extremely useful if we could come up with a general formula that says that such-and-such a sum of rotations defined by a small set of “simple” spindling distances (square roots of integers, say) equals a new spindling distance that is also simple. Realistically, if 6-chromatic unit-distance graphs do exist then they are awfully likely to be way too large to be discoverable by the techniques that got us to 5, so we may need new tricks like this.
A related question, which may be more answerable using the algebraic approach: is it the case that whenever a pentagon of this form exists, there is also a small polygon (maybe not quite a pentagon, but not much more) in which again there is only one edge not in the ring but this time the edge is between vertices at the same distance from the origin? If so, that would let us avoid having to consider spindling angles defined by pairs of points at different distances from the origin – they could be constructed at will from angles defined by pairs at the same distance.
To get to 6-chromatic graphs I would suggest spindling on the point . This point is easy to find in existing graphs by combining Moser spindals and it introduces the ring generator
. This point is easy to find in existing graphs by combining Moser spindals and it introduces the ring generator 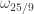 . The factor of five eliminates all linear 5-colourings. That may not be enough to eliminate non-linear 5-colourings but it is a start. I don’t think current methods (computational or otherwise) allow us to explore this much further at present.
. The factor of five eliminates all linear 5-colourings. That may not be enough to eliminate non-linear 5-colourings but it is a start. I don’t think current methods (computational or otherwise) allow us to explore this much further at present.
I have a program that finds all the loops but it returns too many. There are equivalences by reordering and rotating. I would need to reduce them to equivalence classes to make sense of the output. I may find time to do that later.
It is an interesting thing to explore but I dont know how much it will tell us about colourings.
The periodic form of 4-colourings is still mysterious. Given that 8/3 is the same colour as zero you can conclude that there is a periodicity of 8 over the whole ring , i.e.
, i.e. 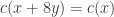 for all elements
for all elements  and
and  of the ring. Proof:
of the ring. Proof:
Start with for all 4-colourings
for all 4-colourings
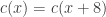

 for
for  giving
giving
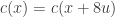 for all
for all  and for all numbers
and for all numbers  of unit modulus $
of unit modulus $
By translation symmetry
Apply three times
The elements of unit modulus generate rotational symmetries so
Substitute back
The set of numbers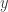 such that for all
such that for all  ,
, 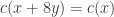 form an additive group because if
form an additive group because if  and
and  for all
for all  latex c(x) = c(x+8z) = c(x+8z+8t) = c(x + 8(z+t)) $
latex c(x) = c(x+8z) = c(x+8z+8t) = c(x + 8(z+t)) $ for all
for all  and
and 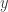 in the ring
in the ring  (and any ring that contains it) when
(and any ring that contains it) when  is a 4-colouring. QED.
is a 4-colouring. QED.
Since the elements of unit modulus generate the whole ring by addition it follows that
Note that we did not lose the original because this follows from 0 and 1/3 being elements of the ring.
because this follows from 0 and 1/3 being elements of the ring.
However, we still lack a human proof that . Could the unplanned edges be essential to show this?
. Could the unplanned edges be essential to show this?
“Could the unplanned edges be essential to show this?” I’m betting that they are.
The virtue I’m seeing of thinking in terms of loops is that the loops are of bounded size, whereas (if I’m understanding correctly) the rings include points that can take an arbitrary number of unit-distance steps to reach from the origin by adding generating vectors. Can the algebraic approach be used to explore bounded sets of this form?
As for 5/3, yes, that makes a lot of sense. I don’t think anyone has looked geometrically at that angle yet to see if it generates any unplanned edges.
As regards equivalence classes, probably simplest would be to do it as the last step – what matters is just the distances of the two points from the origin – if they are 1 apart then that defines the angle.
I don’t think the unplanned edges are at play here as they only appear in while
while 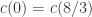 already holds in
already holds in 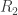 .
.
You are right Tamas. I should have seen that.
Ah yes. Do we know that there are no unplanned edges in R_2 ? I define an unplanned edge just as one whose vertices are at different distances from the origin, obviously excluding ones that are rotations of edges in R_1.
We do know that all edges in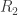 are formed as integer powers of
are formed as integer powers of  and
and  . I even have an informal proof of it in the wiki under the heading “units” on this page
. I even have an informal proof of it in the wiki under the heading “units” on this page
http://michaelnielsen.org/polymath1/index.php?title=Algebraic_formulation_of_Hadwiger-Nelson_problem
My mistake not to see that.
The effect of the unplanned edges in or other rings may still be of interest of course.
or other rings may still be of interest of course.