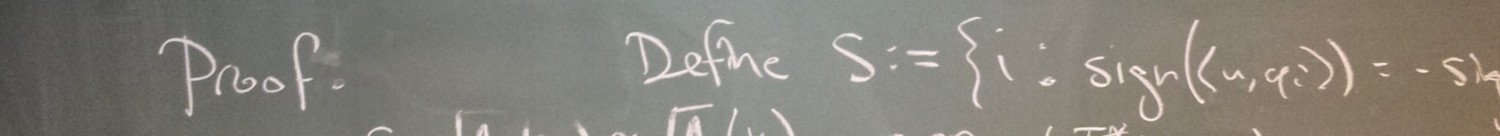Phase retrieval from very few measurements

Before the AIM meeting last month, I posted a paper on the arXiv that I wrote with Matt Fickus, Aaron Nelson and Yang Wang. This paper provides some very interesting results for phase retrieval in the setting where you wish to use as few intensity measurements as possible. There are really three different types of results in this paper, and they are partitioned into three different sections accordingly.

— 4M-4 injective intensity measurements —

Recall that Bodmann and Hammen provide a construction of vectors in which yield injective intensity measurements. Such an explicit construction is rather interesting because is conjectured to be the smallest for which this is even possible. From my perspective, any insight into the structure of such ensembles could lead to a deeper understanding of what it takes to be injective in the complex case, and so such constructions are particularly important.

In our paper, we provide a second construction of injective intensity measurements, and our method for proving injectivity was very different from the Bodmann-Hammen approach. Specifically, it is not clear if the Bodmann-Hammen construction has an efficient reconstruction algorithm, whereas for our construction, injectivity is essentially proved by applying a particular reconstruction algorithm that we designed in concert with the ensemble. We used several key ideas in our design, and I’ll briefly discuss them here.

First, given an -dimensional vector , embed this vector in by indexing the entries with and padding with zeros. Then we can consider the even extension of , namely (the sum of with its reversal). One of our key ideas is that the circular autocorrelation of this even extension almost determines up to global phase (it actually completely determines in the real case, and here the embedding would be in ). In the complex case, is completely determined by the circular autocorrelations of and , where is a modulation operator. Next, the Fourier transform of the circular autocorrelation is the modulus squared of the Fourier transform, and so these circular autocorrelations can be viewed as the inverse Fourier transforms of certain intensity measurements. Furthermore, the fact that our functions are even by construction produces a lot of redundancy in these intensity measurements. Overall, the autocorrelations (and hence the desired signal) can be determined from intensity measurements with and for (here, denotes a discrete cosine function). However, this is a total of intensity measurements, as opposed to the promised . Interestingly, two of these measurements are actually determined by the other because the circular autocorrelations of and have certain entries in common (specifically the entries at and ).

For me, the most bizarre feature of our proof is this last step – after establishing that our signal is completely determined from intensity measurements, we showed that of these can be removed due to redundancy. Why is this bizarre? Because the Bodmann-Hammen construction does the same thing. Their measurement vectors are identified with equally spaced points on two different circles, totaling points (measurement vectors), and then they orient the circles so that they intersect at two of these points, producing the desired redundancy. Also, recall that Balan, Casazza and Edidin’s original result on injective generic ensembles used vectors instead of (which has since been rectified at the AIM workshop, but I’m still waiting to read a write-up of the proof). It is unclear to me whether there is something fundamentally important about as a stepping stone to . I don’t have enough evidence to formulate a conjecture, but I will pose the natural problem:

Problem. Suppose yields injective intensity measurements. Does there necessarily exist a subcollection of size which also yields injective intensity measurements?

— Almost injectivity —

Consider the identity basis along with the all-ones vector. This ensemble does not yield injective intensity measurements because, for example, produces the same intensity measurements as . However, a signal cannot be confused with another signal if the possible sums and differences of its coordinates are all distinct in absolute value (other than the obvious pairs); note that almost every signal has this property. Such ensembles are quite common in the real world, but there isn’t much theory available to evaluate them. As such, our paper studies a notion of almost injectivity, which means that almost every signal is uniquely determined by the intensity measurements.

Focusing on the real case, we devise an analog to the complement property for injectivity. Recall that the complement property says that for any partition into two subcollections, one of these subcollections must span. In the almost injective version, the characterization is that for any nontrivial partition into two subcollections, the sum of the ranks of these subcollections must be greater than (additional mild, technical conditions must also be satisfied, but these aren’t as interesting).

Additionally, we find this property to be particularly easy to find in certain ensembles of measurement vectors. For example, it is not difficult to see that appending the all-ones vector to the identity basis produces an ensemble which satisfies this property, corroborating our intuition from earlier. As another example, in the paper, we show that every unit norm tight frame of $N$ vectors in $M$-dimensional real space with relatively prime to satisfies our property, thereby yielding almost injective intensity measurements. To me, this is a rather striking result because there are many constructions of such frames (for example, spectral tetris, and actually, this paper constructs all such frames explicitly). As such, we can explictly construct an entire continuum of almost injective ensembles, whereas I doubt we will find this many explicit constructions of injective ensembles. Considering this disparity, I think more work needs to be done on almost injectivity. (Certainly, almost injectivity is just as good for practitioners!) For example:

Problem. What are other sufficient conditions for almost injectivity?

— The computational complexity of phase retrieval —

While almost injective ensembles seem relatively easy to construct, in some cases, it is difficult to algorithmically perform phase retrieval with them. In the last section of our paper, we show that whenever you have almost injective measurement vectors in , it is NP-hard to decide whether a given list of numbers are feasible intensity measurements, let alone to perform phase retrieval. In particular, if you could perform phase retrieval with any such ensemble in polynomial time, then you could use that algorithm to solve the subset-sum problem in polynomial time (also, this would imply P=NP). As such, we shouldn’t expect intensity measurements to be enough for efficient phase retrieval. We suspect the same holds in the complex case with intensity measurements.

Throughout the theory of phase retrieval, there are various thresholds on the number of measurement vectors, each characterizing some aspect of the ensemble’s performance. For example, in the real case, no ensemble of size is almost injective, whereas almost every ensemble of size is. For injectivity in the real case, is the threshold, and in the complex case, is conjectured to be the threshold. Our result establishes that there’s another “phase transition” to consider regarding computational complexity. In the real case, we already know there exist ensembles of size which enable efficient phase retrieval. As such, for each , there is a smallest number for which there exists an ensemble of size which enables efficient phase retrieval. Additionally, for almost every ensemble of measurement vectors, the corresponding outer products form a basis for the space of self-adjoint operators, and so phase retrieval can be efficiently solved in such cases by solving a linear system. As such, there is also a smallest number for which almost every ensemble of size enables efficient phase retrieval. We already know that PhaseLift performs phase retrieval for a very large proportion of ensembles of size , but is there an alternative that succeeds even more frequently in this regime? In particular:

Problem. Does ?